icdf

逆累積分布関数

構文

x = icdf(name,p,A)

x = icdf(name,p,A,B)

x = icdf(name,p,A,B,C)

x = icdf(name,p,A,B,C,D)

x = icdf(pd,p)

説明

x = icdf(name,p,A) は、name および分布パラメーター A で指定された 1 パラメーター分布族について、p の確率値で評価した逆累積分布関数 (icdf) を返します。

x = icdf(name,p,A,B) は、name と分布パラメーター A および B で指定された 2 パラメーターの分布族について、p の確率値で評価した icdf を返します。

x = icdf(name,p,A,B,C) は、name と分布パラメーター A、B および C で指定された 3 パラメーターの分布族について、p の確率値で評価した icdf を返します。

x = icdf(name,p,A,B,C,D) は、name と分布パラメーター A、B、C および D で指定された 4 パラメーターの分布族について、p の確率値で評価した icdf を返します。

x = icdf(pd,p) は、p の確率値で評価した、確率分布オブジェクト pd の icdf 関数を返します。

例

分布名とパラメーターを指定した正規分布の逆累積分布関数の計算

分布名 'Normal' と分布パラメーターを指定して、正規分布の icdf 値を計算します。

入力ベクトル p を定義して、icdf を計算する確率値を格納します。

p = [0.1,0.25,0.5,0.75,0.9];

平均 $$\mu$$ が 1、標準偏差 $$\sigma$$ が 5 に等しい正規分布の icdf 値を計算します。

mu = 1;
sigma = 5;
y = icdf('Normal',p,mu,sigma)

y = 1×5

   -5.4078   -2.3724    1.0000    4.3724    7.4078

y の各値は、入力ベクトル x の値に対応しています。たとえば、"x" 値が 1 の場合、対応する icdf 値 "y" は 7.4078 です。

分布オブジェクトを使用した正規分布の逆累積分布関数の計算

正規分布オブジェクトを作成し、そのオブジェクトを使用して正規分布の icdf 値を計算します。

平均 $$\mu$$ が 1、標準偏差 $$\sigma$$ が 5 に等しい正規分布オブジェクトを作成します。

mu = 1;
sigma = 5;
pd = makedist('Normal','mu',mu,'sigma',sigma);

入力ベクトル p を定義して、icdf を計算する確率値を格納します。

p = [0.1,0.25,0.5,0.75,0.9];

"p" の値における正規分布の icdf 値を計算します。

x = icdf(pd,p)

x = 1×5

   -5.4078   -2.3724    1.0000    4.3724    7.4078

"x" の各値は、入力ベクトル "p" の値に対応しています。たとえば、"p" の値が 0.9 である場合、対応する icdf 値 "x" は 7.4078 です。

ポアソン分布 icdf の計算

レート パラメーター $$\lambda$$ が 2 に等しいポアソン分布オブジェクトを作成します。

lambda = 2;
pd = makedist('Poisson','lambda',lambda);

入力ベクトル p を定義して、icdf を計算する確率値を格納します。

p = [0.1,0.25,0.5,0.75,0.9];

p の値におけるポアソン分布の icdf 値を計算します。

x = icdf(pd,p)

x = 1×5

     0     1     2     3     4

x の各値は、入力ベクトル p の値に対応しています。たとえば、p の値が 0.9 である場合、対応する icdf 値 x は 4 です。

また、確率分布オブジェクトを作成せずに同じ icdf 値を計算することもできます。関数 icdf を使用し、レート パラメーター $$\lambda$$ について同じ値を使用してポアソン分布を指定します。

x2 = icdf('Poisson',p,lambda)

x2 = 1×5

     0     1     2     3     4

icdf の値は、確率分散オブジェクトを使用して計算した値と同じです。

標準正規分布の棄却限界値を計算する

標準正規分布オブジェクトを作成します。

pd = makedist('Normal')

pd = 
  NormalDistribution

  Normal distribution
       mu = 0
    sigma = 1

上限および下限の 2.5% の値を計算して、標準正規分布をもつ検定統計量の有意水準 5% における棄却限界値を判定します。

x = icdf(pd,[.025,.975])

x = 1×2

   -1.9600    1.9600

累積分布関数をプロットして棄却限界を塗りつぶします。

p = normspec(x,0,1,'outside')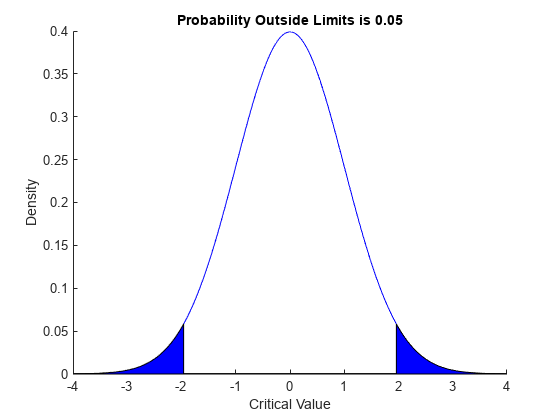

p = 0.0500

入力引数

name — 確率分布名

文字ベクトルまたは string スカラーによる確率分布名

確率分布名。次の表のいずれかの確率分布名を指定します。

name	分布	入力パラメーター A	入力パラメーター B	入力パラメーター C	入力パラメーター D
'Beta'	ベータ分布	1 番目の形状パラメーター a	2 番目の形状パラメーター b	該当なし	該当なし
'Binomial'	二項分布	試行回数 n	各試行の成功確率 p	該当なし	該当なし
'BirnbaumSaunders'	バーンバウム・サンダース分布	スケール パラメーター β	形状パラメーター γ	該当なし	該当なし
'Burr'	ブール型 XII 分布	スケール パラメーター α	1 番目の形状パラメーター c	2 番目の形状パラメーター k	該当なし
'Chisquare' または 'chi2'	カイ二乗分布	自由度 ν	該当なし	該当なし	該当なし
'Exponential'	指数分布	平均値 μ	該当なし	該当なし	該当なし
'Extreme Value' または 'ev'	極値分布	位置パラメーター μ	スケール パラメーター σ	該当なし	該当なし
'F'	F 分布	分子の自由度 ν1	分母の自由度 ν2	該当なし	該当なし
'Gamma'	ガンマ分布	形状パラメーター a	スケール パラメーター b	該当なし	該当なし
'Generalized Extreme Value' または 'gev'	一般化極値分布	形状パラメーター k	スケール パラメーター σ	位置パラメーター μ	該当なし
'Generalized Pareto' または 'gp'	一般化パレート分布	裾の指数 (形状) パラメーター k	スケール パラメーター σ	しきい値 (位置) パラメーター μ	該当なし
'Geometric'	幾何分布	確率パラメーター p	該当なし	該当なし	該当なし
'Half Normal' または 'hn'	半正規分布	位置パラメーター μ	スケール パラメーター σ	該当なし	該当なし
'Hypergeometric' または 'hyge'	超幾何分布	母集団のサイズ m	母集団内で対象となる特徴をもつ項目の個数 k	抽出した標本の個数 n	該当なし
'InverseGaussian'	逆ガウス分布	スケール パラメーター μ	形状パラメーター λ	該当なし	該当なし
'Logistic'	ロジスティック分布	平均値 μ	スケール パラメーター σ	該当なし	該当なし
'LogLogistic'	対数ロジスティック分布	対数値の平均 μ	対数値のスケール パラメーター σ	該当なし	該当なし
'LogNormal'	対数正規分布	対数値の平均 μ	対数値の標準偏差 σ	該当なし	該当なし
'Loguniform'	対数一様分布	下限端点 (最小) a	上限端点 (最大) b	該当なし	該当なし
'Nakagami'	仲上分布	形状パラメーター μ	スケール パラメーター ω	該当なし	該当なし
'Negative Binomial' または 'nbin'	負の二項分布	成功回数 r	1 回の試行における成功確率 p	該当なし	該当なし
'Noncentral F' または 'ncf'	非心 F 分布	分子の自由度 ν1	分母の自由度 ν2	非心度パラメーター δ	該当なし
'Noncentral t' または 'nct'	非心 t 分布	自由度 ν	非心度パラメーター δ	該当なし	該当なし
'Noncentral Chi-square' または 'ncx2'	非心カイ二乗分布	自由度 ν	非心度パラメーター δ	該当なし	該当なし
'Normal'	正規分布	平均値 μ	標準偏差 σ	該当なし	該当なし
'Poisson'	ポアソン分布	平均値 λ	該当なし	該当なし	該当なし
'Rayleigh'	レイリー分布	スケール パラメーター b	該当なし	該当なし	該当なし
'Rician'	ライス分布	非心度パラメーター s	スケール パラメーター σ	該当なし	該当なし
'Stable'	安定分布	1 番目の形状パラメーター α	2 番目の形状パラメーター β	スケール パラメーター γ	位置パラメーター δ
'T'	スチューデントの t 分布	自由度 ν	該当なし	該当なし	該当なし
'tLocationScale'	t 位置-スケール分布	位置パラメーター μ	スケール パラメーター σ	形状パラメーター ν	該当なし
'Uniform'	一様分布 (連続)	下限端点 (最小) a	上限端点 (最大) b	該当なし	該当なし
'Discrete Uniform' または 'unid'	一様分布 (離散)	最大観測可能値 n	該当なし	該当なし	該当なし
'Weibull' または 'wbl'	ワイブル分布	スケール パラメーター a	形状パラメーター b	該当なし	該当なし

例: 'Normal'

p — icdf を評価する確率値

スカラー値 | スカラー値の配列

icdf を評価する確率値。範囲 [0,1] のスカラー値またはスカラー値の配列を指定します。

入力引数 p、A、B、C および D の 1 つ以上が配列である場合、配列のサイズは同じでなければなりません。この場合、icdf は配列入力と同じサイズの定数配列に各スカラー入力を拡張します。各分布の A、B、C および D の定義については、name を参照してください。

例: [0.1,0.25,0.5,0.75,0.9]

データ型: single | double

A — 1 番目の確率分布パラメーター

スカラー値 | スカラー値の配列

1 番目の確率分布パラメーター。スカラー値またはスカラー値の配列を指定します。

入力引数 p、A、B、C および D の 1 つ以上が配列である場合、配列のサイズは同じでなければなりません。この場合、icdf は配列入力と同じサイズの定数配列に各スカラー入力を拡張します。各分布の A、B、C および D の定義については、name を参照してください。

データ型: single | double

B — 2 番目の確率分布パラメーター

スカラー値 | スカラー値の配列

2 番目の確率分布パラメーター。スカラー値またはスカラー値の配列を指定します。

入力引数 p、A、B、C および D の 1 つ以上が配列である場合、配列のサイズは同じでなければなりません。この場合、icdf は配列入力と同じサイズの定数配列に各スカラー入力を拡張します。各分布の A、B、C および D の定義については、name を参照してください。

データ型: single | double

C — 3 番目の確率密度パラメーター

スカラー値 | スカラー値の配列

3 番目の確率分布パラメーター。スカラー値またはスカラー値の配列を指定します。

入力引数 p、A、B、C および D の 1 つ以上が配列である場合、配列のサイズは同じでなければなりません。この場合、icdf は配列入力と同じサイズの定数配列に各スカラー入力を拡張します。各分布の A、B、C および D の定義については、name を参照してください。

データ型: single | double

D — 4 番目の確率分布パラメーター

スカラー値 | スカラー値の配列

4 番目の確率分布パラメーター。スカラー値またはスカラー値の配列を指定します。

入力引数 p、A、B、C および D の 1 つ以上が配列である場合、配列のサイズは同じでなければなりません。この場合、icdf は配列入力と同じサイズの定数配列に各スカラー入力を拡張します。各分布の A、B、C および D の定義については、name を参照してください。

データ型: single | double

pd — 確率分布

確率分布オブジェクト

確率分布。次の表のいずれかの確率分布オブジェクトを指定します。

分布オブジェクト	確率分布オブジェクトを作成するための関数またはアプリ
BetaDistribution	makedist、fitdist、Distribution Fitter
BinomialDistribution	makedist、fitdist、Distribution Fitter
BirnbaumSaundersDistribution	makedist、fitdist、Distribution Fitter
BurrDistribution	makedist、fitdist、Distribution Fitter
ExponentialDistribution	makedist、fitdist、Distribution Fitter
ExtremeValueDistribution	makedist、fitdist、Distribution Fitter
GammaDistribution	makedist、fitdist、Distribution Fitter
GeneralizedExtremeValueDistribution	makedist、fitdist、Distribution Fitter
GeneralizedParetoDistribution	makedist、fitdist、Distribution Fitter
HalfNormalDistribution	makedist、fitdist、Distribution Fitter
InverseGaussianDistribution	makedist、fitdist、Distribution Fitter
KernelDistribution	fitdist、Distribution Fitter
LogisticDistribution	makedist、fitdist、Distribution Fitter
LoglogisticDistribution	makedist、fitdist、Distribution Fitter
LognormalDistribution	makedist、fitdist、Distribution Fitter
LoguniformDistribution	makedist
MultinomialDistribution	makedist
NakagamiDistribution	makedist、fitdist、Distribution Fitter
NegativeBinomialDistribution	makedist、fitdist、Distribution Fitter
NormalDistribution	makedist、fitdist、Distribution Fitter
裾が一般化パレート分布になっている区分的分布	paretotails
PiecewiseLinearDistribution	makedist
PoissonDistribution	makedist、fitdist、Distribution Fitter
RayleighDistribution	makedist、fitdist、Distribution Fitter
RicianDistribution	makedist、fitdist、Distribution Fitter
StableDistribution	makedist、fitdist、Distribution Fitter
tLocationScaleDistribution	makedist、fitdist、Distribution Fitter
TriangularDistribution	makedist
UniformDistribution	makedist
WeibullDistribution	makedist、fitdist、Distribution Fitter

出力引数

x — icdf の値

スカラー値 | スカラー値の配列

icdf の値。スカラー値またはスカラー値の配列として返されます。x は、必要なスカラー拡張後の p と同じサイズになります。x の各要素は、分布パラメーター (A、B、C、および D) 内の対応する要素または確率分布オブジェクト (pd) によって指定される分布の icdf 値で、p 内の対応する要素で評価されています。

代替機能

icdf は、名前 name によって指定された分布、または確率分布オブジェクト pd のいずれも受け入れる汎用関数です。正規分布の場合は norminv、二項分布の場合は binoinv など、分布特有の関数を使用する方が高速です。分布特有の関数の一覧については、サポートされている分布を参照してください。

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意事項および制限事項:

• 入力引数 name はコンパイル時の定数でなければなりません。たとえば、正規分布を使用するには、coder.Constant('Normal') を codegen (MATLAB Coder) の -args の値に含めます。

• 入力引数 pd は、ベータ分布、指数分布、極値分布、対数正規分布、正規分布、ワイブル分布の近似確率分布オブジェクトとなります。確率分布を関数 fitdist の標本データにあてはめることで、pd を作成します。たとえば、確率分布オブジェクトのコードの生成を参照してください。

コード生成の詳細については、コード生成の紹介および一般的なコード生成のワークフローを参照してください。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

この関数は、GPU 配列を完全にサポートします。詳細は、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2006a より前に導入

参考

cdf | mle | pdf | random | makedist | fitdist | Distribution Fitter | paretotails

トピック

• 確率分布の操作
• サポートされている分布

×

例を開く

この例の変更されたバージョンがあります。編集された方の例を開きますか?

いいえ、変更されたバージョンを上書きします。 はい