半正規分布

概要

半正規分布は、折り返された正規分布および打ち切られた正規分布の特殊なケースです。半正規分布の応用には、測定データや寿命データのモデル化などがあります。

パラメーター

半正規分布では、次のパラメーターを使用します。

パラメーター	説明
$$-\infty <\mu <\infty$$	位置パラメーター
$$\sigma \ge 0$$	スケール パラメーター

半正規分布のサポートは x ≥ μ です。

半正規確率分布オブジェクト HalfNormalDistribution を作成するには、パラメーター値を指定して makedist を使用します。半正規確率分布オブジェクトを標本データに当てはめるには、fitdist を使用します。確率分布オブジェクトを作成せずに標本データから半正規分布のパラメーター値を推定するには、mle を使用します。確率分布の処理の詳細については、確率分布の操作を参照してください。

Statistics and Machine Learning Toolbox™ における半正規分布の実装では、固定値の位置パラメーター μ を仮定しています。したがって、半正規分布を標本データに当てはめる際、fitdist も mle もパラメーター μ の値を推定しません。パラメーター μ の値は、名前と値のペアの引数 'mu' を使用して指定できます。fitdist と mle の両方で、引数 'mu' の既定値は 0 です。

確率密度関数

半正規分布の確率密度関数 (pdf) は次のようになります。

$$y=f\left(x|\mu ,\sigma \right)=\sqrt{\frac{2}{\pi }}\frac{1}{\sigma }{e}^{-\frac{1}{2}{\left(\frac{x-\mu }{\sigma }\right)}^2};x\ge \mu ,$$

ここで、μ は位置パラメーター、σ はスケール パラメーターです。x ≤ μ である場合、pdf は定義されません。

半正規分布の pdf を計算するには、fitdist または makedist を使用して HalfNormalDistribution 確率分布オブジェクトを作成し、pdf メソッドを使用してオブジェクトを操作します。

半正規確率分布の pdf

この例では、パラメーター mu および sigma の値を変更すると pdf の形状がどのように変化するかを示します。

パラメーターが異なる 4 つの確率分布オブジェクトを作成します。

pd1 = makedist('HalfNormal');
pd2 = makedist('HalfNormal','mu',0,'sigma',2);
pd3 = makedist('HalfNormal','mu',0,'sigma',3);
pd4 = makedist('HalfNormal','mu',0,'sigma',5);

各分布の確率密度関数 (pdf) を計算します。

x = 0:0.1:10;
pdf1 = pdf(pd1,x);
pdf2 = pdf(pd2,x);
pdf3 = pdf(pd3,x);
pdf4 = pdf(pd4,x);

同じ図に pdf をプロットします。

figure;
plot(x,pdf1,'r','LineWidth',2)
hold on;
plot(x,pdf2,'k:','LineWidth',2);
plot(x,pdf3,'b-.','LineWidth',2);
plot(x,pdf4,'g--','LineWidth',2);
legend({'mu = 0, sigma = 1','mu = 0, sigma = 2',...
    'mu = 0, sigma = 3','mu = 0, sigma = 5'},'Location','NE');
hold off;

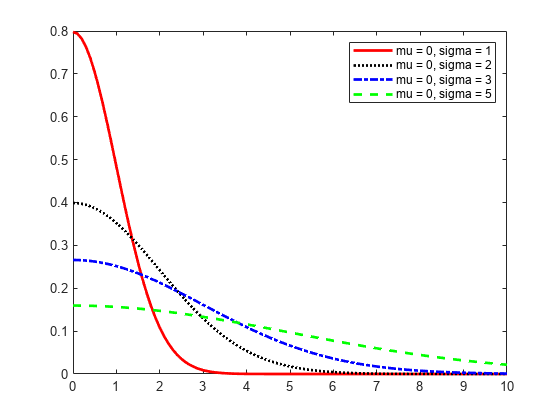
sigma が大きくなると、曲線が平らになり、ピーク値が小さくなります。

累積分布関数

半正規分布の累積分布関数 (cdf) は次のようになります。

$$y=F\left(x\right)=erf\left(\frac{x-\mu }{\sqrt{2}\sigma }\right)=2\Phi \left(\frac{x-\mu }{\sigma }\right)-1;x\ge \mu ,$$

ここで、μ は位置パラメーター、σ はスケール パラメーター、erf(•) は誤差関数、Φ(•) は標準正規分布の cdf です。x ≤ μ である場合、cdf は定義されません。

半正規分布の cdf を計算するには、fitdist または makedist を使用して HalfNormalDistribution 確率分布オブジェクトを作成し、cdf メソッドを使用してオブジェクトを操作します。

半正規確率分布の cdf

この例では、パラメーター mu および sigma の値を変更すると cdf の形状がどのように変化するかを示します。

パラメーターが異なる 4 つの確率分布オブジェクトを作成します。

pd1 = makedist('HalfNormal');
pd2 = makedist('HalfNormal','mu',0,'sigma',2);
pd3 = makedist('HalfNormal','mu',0,'sigma',3);
pd4 = makedist('HalfNormal','mu',0,'sigma',5);

各確率分布の累積分布関数 (cdf) を計算します。

x = 0:0.1:10;
cdf1 = cdf(pd1,x);
cdf2 = cdf(pd2,x);
cdf3 = cdf(pd3,x);
cdf4 = cdf(pd4,x);

同じ図に 4 つの cdf をすべてプロットします。

figure;
plot(x,cdf1,'r','LineWidth',2)
hold on;
plot(x,cdf2,'k:','LineWidth',2);
plot(x,cdf3,'b-.','LineWidth',2);
plot(x,cdf4,'g--','LineWidth',2);
legend({'mu = 0, sigma = 1','mu = 0, sigma = 2',...
    'mu = 0, sigma = 3','mu = 0, sigma = 5'},'Location','SE');
hold off;

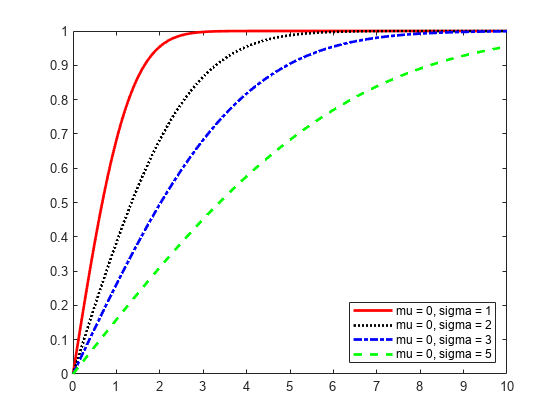
sigma が大きくなると、cdf の曲線が平らになります。

記述統計

半正規分布の平均は次のようになります。

$$\text{mean}=\mu +\sigma \sqrt{\frac{2}{\pi },}$$

ここで、μ は位置パラメーター、σ はスケール パラメーターです。

半正規分布の分散は次のようになります。

$$\mathrm{var}={\sigma }^2\left(1-\frac{2}{\pi }\right),$$

ここで、σ はスケール パラメーターです。

他の分布との関係

平均 μ が 0、標準偏差 σ が 1 に等しい標準正規分布に確率変数 Z が従っている場合、$$X=\mu +\sigma \left|Z\right|$$ はパラメーター μ および σ をもつ半正規分布になります。

参照

[1] Cooray, K. and M.M.A. Ananda. “A Generalization of the Half-Normal Distribution with Applications to Lifetime Data.” Communications in Statistics – Theory and Methods. Vol. 37, Number 9, 2008, pp. 1323–1337.

[2] Pewsey, A. “Large-Sample Inference for the General Half-Normal Distribution.” Communications in Statistics – Theory and Methods. Vol. 31, Number 7, 2002, pp. 1045–1054.

参考

HalfNormalDistribution

関連するトピック

• 確率分布の操作
• サポートされている分布