mle

最尤推定

ページ内をすべて折りたたむ

構文

phat = mle(data)

phat = mle(data,Name,Value)

[phat,pci] = mle(___)

説明

phat = mle(data) は、標本データ data を使用して、正規分布のパラメーターに対する最尤推定 (MLE) を返します。

phat = mle(data,Name,Value) では、1 つ以上の名前と値の引数を使用してオプションを指定します。

たとえば、次の名前と値の引数 Distribution、pdf、logpdf、nloglf のうちの 1 つを使用して、分布タイプを指定できます。

組み込み分布の MLE を計算するには、Distribution を使用して、分布タイプを指定します。たとえば、'Distribution','Beta' は、ベータ分布の MLE を計算するように指定します。
カスタム分布の MLE を計算するには、pdf、logpdf、または nloglf を使用して分布を定義し、Start を使用して初期パラメーター値を指定します。

例

[phat,pci] = mle(___) は、前の構文におけるいずれかの入力引数の組み合わせを使用して、パラメーターの信頼区間も返します。

例

すべて折りたたむ

組み込み分布の MLE の計算

ライブスクリプトを開く

名前と値の引数 Distribution を使用して指定した組み込み分布の MLE を計算します。

標本データを読み込みます。

load carbig

変数 MPG には、さまざまな自動車モデルのガロンあたりの走行マイル数が含まれます。

MPG データのヒストグラムを描画します。

 histogram(MPG)

Figure contains an axes object. The axes object contains an object of type histogram.

分布はやや右に歪んでいます。正規分布などの対称分布は適切な当てはめにならない場合があります。

MPG データのブール型 XII 分布のパラメーターを推定します。

phat = mle(MPG,'Distribution','burr')

phat = 1×3

   34.6447    3.7898    3.5722

スケールパラメーター α の MLE は 34.6447 です。ブール型 XII 分布の 2 つの形状パラメーター $c$ および $k$ の推定値は、それぞれ 3.7898 および 3.5722 です。

MLE および信頼区間の計算

ライブスクリプトを開く

試行回数 $n$ = 20 および成功確率 $p$ = 0.75 の二項分布から 100 個のランダムな観測値を生成します。

rng('default') % For reproducibility
data = binornd(20,0.75,100,1);

シミュレーションを実行した標本データを使用して成功確率と 99% の信頼限界を推定します。二項分布の試行回数 (NTrials) を指定する必要があります。

[phat,pci] = mle(data,'Distribution','binomial','NTrials',20, ...
    'Alpha',.01)

phat = 
0.7615

pci = 2×1

    0.7361
    0.7856

成功確率の推定値は 0.7615 であり、99% 信頼区間の下限と上限はそれぞれ 0.7361 と 0.7856 です。この区間は、データのシミュレーションの実行に使用される真の値に対応します。

カスタム確率密度関数 (pdf) の当てはめ

ライブスクリプトを開く

自由度が 8、非心度パラメーターが 3 の非心カイ二乗分布から、サイズが 1000 の標本データを生成します。

rng default % for reproducibility
x = ncx2rnd(8,3,1000,1);

標本データから非心カイ二乗分布のパラメーターを推定します。名前と値の引数 Distribution は、非心カイ二乗分布をサポートしていません。そのため、名前と値の引数 pdf および関数 ncx2pdf を使用して、カスタムの非心カイ二乗 pdf を定義する必要があります。カスタム分布には初期パラメーター値 (名前と値の引数 Start) も指定する必要があります。

[phat,pci] = mle(x,'pdf',@(x,v,d)ncx2pdf(x,v,d),'Start',[1,1])

phat = 1×2

    8.1052    2.6693

pci = 2×2

    7.1120    1.6025
    9.0983    3.7362

自由度の推定値は 8.1052、非心度パラメーターの推定値は 2.6693 です。自由度の 95% の信頼区間は (7.1120,9.0983)、非心度パラメーターの区間は (1.6025,3.7362) です。この信頼区間には、真のパラメーター値 8 および 3 が含まれています。

カスタム対数確率密度関数 (pdf) の当てはめ

ライブスクリプトを開く

標本データを読み込みます。

load('readmissiontimes.mat');

このデータには、100 人の患者の再入院時間を示す ReadmissionTime が含まれています。このデータは、シミュレーションされたものです。

スケールパラメーター lambda と形状パラメーター k をもつワイブル分布のカスタム対数 pdf を定義します。

custlogpdf = @(data,lambda,k) ...
    log(k) - k*log(lambda) + (k-1)*log(data) - (data/lambda).^k;

カスタム分布のパラメーターを推定し、初期パラメーター値 (名前と値の引数 Start) を指定します。

phat = mle(ReadmissionTime,'logpdf',custlogpdf,'Start',[1,0.75])

phat = 1×2

    7.5727    1.4540

カスタム分布のスケールパラメーターと形状パラメーターはそれぞれ 7.5727 と 1.4540 です。

カスタムな負の対数尤度関数の当てはめ

ライブスクリプトを開く

標本データを読み込みます。

load('readmissiontimes.mat')

このデータには、100 人の患者の再入院時間を示す ReadmissionTime が含まれています。このデータは、シミュレーションされたものです。

パラメーター lambda をもつポアソン分布のカスタムな負の対数尤度関数を定義します。ここで 1/lambda は分布の平均値です。カスタム関数で打ち切り情報の logical ベクトルおよびデータ頻度の整数ベクトルを使用しない場合でも、これらの値を受け入れる関数を定義する必要があります。

custnloglf = @(lambda,data,cens,freq) ...
    - length(data)*log(lambda) + sum(lambda*data,'omitnan');

カスタム分布のパラメーターを推定し、初期パラメーター値 (名前と値の引数 Start) を指定します。

phat = mle(ReadmissionTime,'nloglf',custnloglf,'Start',0.05)

phat = 
0.1462

既知パラメーターによる分布の当てはめ

ライブスクリプトを開く

自由度が 10、非心度パラメーターが 5 の非心カイ二乗分布から、サイズが 1000 の標本データを生成します。

rng('default') % For reproducibility
x = ncx2rnd(10,5,1000,1);

非心度パラメーターは値 5 に固定されるとします。標本データから非心カイ二乗分布の自由度を推定します。これを行うため、名前と値の引数 pdf を使用して、カスタムの非心カイ二乗 pdf を定義します。

[phat,pci] = mle(x,'pdf',@(x,v)ncx2pdf(x,v,5),'Start',1)

phat = 
9.9307

pci = 2×1

    9.5626
   10.2989

非心度パラメーターの推定値は 9.9307 であり、95% 信頼区間の下限と上限は 9.5626 と 10.2989 です。この信頼区間には、真のパラメーター値 10 が含まれています。

追加パラメーターによる分布の当てはめ

ライブスクリプトを開く

データのスケールに適合させるためスケールパラメーターをカイ二乗分布に追加し、分布を当てはめます。

自由度が 5 のカイ二乗分布からサイズが 1000 の標本データを生成し、100 という係数でデータをスケーリングします。

rng default % For reproducibility
x = 100*chi2rnd(5,1000,1);

自由度とスケーリング係数を推定します。これを行うため、名前と値の引数 pdf を使用してカスタムなカイ二乗確率密度関数を定義します。密度関数では、データを $s$ でスケーリングするために係数 $1 / s$ が必要です。

[phat,pci] = mle(x,'pdf',@(x,v,s)chi2pdf(x/s,v)/s,'Start',[1,200])

phat = 1×2

    5.1079   99.1681

pci = 2×2

    4.6862   90.1215
    5.5297  108.2146

自由度の推定値は 5.1079、スケールの推定値は 99.1681 です。自由度の 95% の信頼区間は (4.6862,5.5279)、スケールパラメーターの区間は (90.1215,108.2146) です。この信頼区間には、真のパラメーター値 5 および 100 が含まれています。

右側打ち切りデータへのカスタム分布の当てはめ

ライブスクリプトを開く

標本データを読み込みます。

load('readmissiontimes.mat');

このデータには、100 人の患者の再入院時間を示す ReadmissionTime が含まれています。列ベクトル Censored には各患者の打ち切り情報が含まれ、1 は右側打ち切り観測を示し、0 は正確な再入院時間が観測されることを示します。このデータは、シミュレーションされたものです。

パラメーター lambda をもつ指数分布のカスタムな確率密度関数 (pdf) および累積分布関数 (cdf) を定義します。ここで 1/lambda は分布の平均値です。分布を打ち切られたデータセットに当てはめるには、pdf および cdf の両方を関数 mle に渡す必要があります。

custpdf = @(data,lambda) lambda*exp(-lambda*data);
custcdf = @(data,lambda) 1-exp(-lambda*data);

打ち切れらた標本データのカスタム分布のパラメーター lambda を推定します。カスタム分布の初期パラメーター値 (名前と値の引数 Start) を指定します。

phat = mle(ReadmissionTime,'pdf',custpdf,'cdf',custcdf, ...
    'Start',0.05,'Censoring',Censored)

phat = 
0.1096

二重打ち切りデータの MLE の計算

ライブスクリプトを開く

二重打ち切り生存データを生成し、このデータの組み込み分布の MLE を計算します。次に、MLE を使用して確率分布オブジェクトを作成します。

バーンバウム・サンダース分布から故障時間を生成します。

rng('default')  % For reproducibility
failuretime = random('BirnbaumSaunders',0.3,1,[100,1]);

分析は時間 0.1 から開始し、時間 0.9 で終了すると仮定します。この仮定は、0.1 より小さい故障時間は左側打ち切りされ、0.9 より大きい故障時間は右側打ち切りされることを意味します。

各要素が failuretime の対応する観測の打ち切りステータスを示すベクトルを作成します。–1、1、および 0 を使用して、それぞれ左側打ち切り観測値、右側打ち切り観測値、完全に観測された観測値を示します。

L = 0.1;
U = 0.9;
left_censored = (failuretime<L);
right_censored = (failuretime>U);
c = right_censored - left_censored;

二重打ち切りデータの MLE を計算します。名前と値の引数 Censoring を使用して打ち切り情報を指定します。

phat = mle(failuretime,'Distribution','BirnbaumSaunders','Censoring',c)

phat = 1×2

    0.2632    1.3040

関数 makedist を使用し、MLE で確率分布オブジェクトを作成します。

pd = makedist('BirnbaumSaunders','beta',phat(1),'gamma',phat(2))

pd = 
  BirnbaumSaundersDistribution

  Birnbaum-Saunders distribution
     beta = 0.263184
    gamma =    1.304

pd は、BirnbaumSaundersDistribution オブジェクトです。pd のオブジェクト関数を使用して、分布の評価と乱数の生成を実行できます。サポートされるオブジェクト関数を表示します。

methods(pd)

Methods for class prob.BirnbaumSaundersDistribution:

cdf        gather     icdf       iqr        mean       median     negloglik  paramci    pdf        plot       proflik    random     std        truncate   var

たとえば、関数 mean および var を使用して、それぞれ分布の平均と分散を計算します。

mean(pd)

ans = 
0.4869

var(pd)

ans = 
0.3681

区間打ち切りデータの MLE の計算

ライブスクリプトを開く

ワイブル分布に従う機械故障時間を表す標本データを生成します。

rng('default') % For reproducibility
failureTimes = wblrnd(5,2,[200,1]);

観測された故障時間は最も近い秒に丸められた値であると指定します。

observed = round(failureTimes);

observed は区間打ち切りデータです。observed の観測値 t は、事象が時間 t–0.5 の後かつ時間 t+0.5 の前に発生したことを示しています。

打ち切り情報を含む 2 列の行列を作成します。

intervalTimes = [observed-0.5 observed+0.5];

故障時間は正の値である必要があります。eps より小さい値を求め、eps に変更します。

intervalTimes(intervalTimes < eps) = eps;

intervalTimesを使用して、ワイブル分布パラメーターの MLE を求めます。

params = mle(intervalTimes,'Distribution','Weibull')

params = 1×2

    5.0067    2.0049

結果をプロットします。

figure
histogram(observed,'Normalization','pdf')
hold on
x = linspace(0,max(observed));
plot(x,wblpdf(x,params(1),params(2)))
legend('Observed Samples','Fitted Distribution')
hold off

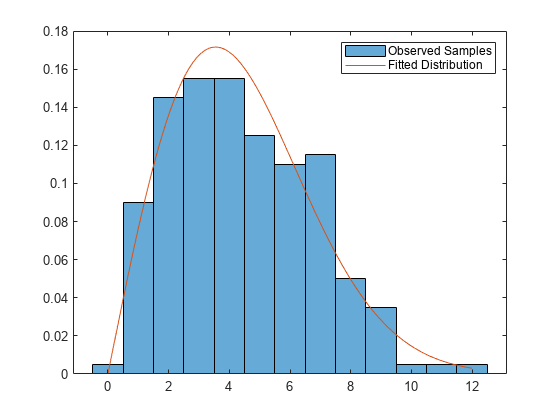
Figure contains an axes object. The axes object contains 2 objects of type histogram, line. These objects represent Observed Samples, Fitted Distribution.

有限のサポートをもつ分布の MLE の計算

ライブスクリプトを開く

有限のサポートをもつ分布から標本を生成し、反復推定処理用にカスタマイズされたオプションで MLE を計算します。

確率密度がゼロになる領域がある分布の場合、mle は密度がゼロになるパラメーターを試す可能性があり、MLE の計算が失敗する原因となります。この問題を回避するため、関数 mle を呼び出すときに、無効な関数値をチェックするオプションをオフにして、パラメーターの境界を指定できます。

スケールパラメーター 1 および形状パラメーター 1 をもつワイブル分布から、サイズが 1000 の標本データを生成します。10 を足して標本を移動させます。

rng('default') % For reproducibility
data = wblrnd(1,1,[1000,1]) + 10;
histogram(data,'Normalization','pdf')

Figure contains an axes object. The axes object contains an object of type histogram.

ヒストグラムに 10 より小さい標本はありません。この分布では 10 より小さい領域の確率がゼロであることを示しています。この分布は 3 パラメーターのワイブル分布で、位置の 3 番目のパラメーターが含まれます (3 パラメーターワイブル分布を参照)。

3 パラメーターのワイブル分布の確率密度関数 (pdf) を定義します。

custompdf = @(x,a,b,c) wblpdf(x-c,a,b);

関数 mle を使用して MLE を計算します。名前と値の引数 Options を指定して、無効な関数値をチェックするオプションをオフにします。また、名前と値の引数 LowerBound および UpperBound を使用してパラメーターの境界を指定します。スケールパラメーターと形状パラメーターは正である必要があります。位置パラメーターは標本データの最小値より小さい必要があります。

params = mle(data,'pdf',custompdf,'Start',[5 5 5], ...
     'Options',statset('FunValCheck','off'), ...
     'LowerBound',[0 0 -Inf],'UpperBound',[Inf Inf min(data)])

params = 1×3

    1.0258    1.0618   10.0004

関数 mle は 3 つのパラメーターの正確な推定値を計算します。反復プロセスに指定するカスタムオプションの詳細については、3 パラメーターワイブル分布の例を参照してください。

入力引数

すべて折りたたむ

`data` — 標本データおよび打ち切り情報
ベクトル | 2 列の行列

標本データおよび打ち切り情報。標本データのベクトルとして、または標本データおよび打ち切り情報からなる 2 列の行列として指定します。

引数 data または名前と値の引数 Censoring のいずれかを使用して、標本データの打ち切り情報を指定できます。data が 2 列の行列の場合、mle は引数 Censoring の値を無視します。

data の観測値の打ち切りタイプに応じて、data をベクトルまたは 2 列の行列として指定します。

完全に観測されたデータ — data を標本データのベクトルとして指定します。
完全に観測された観測値、左側打ち切り観測値、または右側打ち切り観測値を含むデータ — 標本データのベクトルとして data を指定し、各観測値の打ち切り情報を含むベクトルとして名前と値の引数 Censoring を指定します。Censoring ベクトルには 0、-1、および 1 を含められます。それぞれ完全に観測された観測値、左側打ち切り観測値、右側打ち切り観測値を参照します。
区間打ち切り観測値を含むデータ — data を、標本データおよび打ち切り情報からなる 2 列の行列として指定します。data の各行は、各観測値に対する可能な生存時間または故障時間の範囲を指定します。以下の値のいずれかにできます。
- [t,t] — t で完全に観測
- [–Inf,t] — t で左側打ち切り
- [t,Inf] — t で右側打ち切り
- [t₁,t₂] — [t₁,t₂] 間で区間打ち切り (t₁ < t₂)
打ち切られた観測値をサポートしている組み込み分布のリストについては、Censoring を参照してください。
mle は、data 内の NaN 値を無視します。また、打ち切りベクトル (Censoring) または頻度ベクトル (Frequency) に NaN 値が含まれている場合、mle は data 内の対応する行を無視します。

データ型: single | double

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで Name は引数名、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: 'Censoring',Cens,'Alpha',0.01,'Options',Opt は、mle が配列 Cens で指定された打ち切りデータの分布に対するパラメーターを推定して、パラメーター推定の 99% の信頼限界を計算し、構造体 Opt で指定されたアルゴリズム制御パラメーターを使用するように指示します。

組み込み分布を指定するオプション

すべて折りたたむ

`Distribution` — 分布タイプ
`'normal'` (既定値) | 文字ベクトルまたは string スカラーによる分布タイプ

パラメーターを推定する分布タイプ。次の表のいずれかの値として指定します。

`Distribution` の値	分布タイプ	最初のパラメーター	2 番目のパラメーター	3 番目のパラメーター	4 番目のパラメーター
`'Bernoulli'`	ベルヌーイ分布	`p`: それぞれの試行での成功の確率	該当なし	該当なし	該当なし
`'Beta'`	ベータ分布	`a`: 1 番目の形状パラメーター	`b`: 2 番目の形状パラメーター	該当なし	該当なし
`'Binomial'`	二項分布	`p`: それぞれの試行での成功の確率	該当なし	該当なし	該当なし
`'BirnbaumSaunders'`	バーンバウム・サンダース分布	β: スケールパラメーター	γ: 形状パラメーター	該当なし	該当なし
`'Burr'`	ブール型 XII 分布	α: スケールパラメーター	`c`: 1 番目の形状パラメーター	`k`: 2 番目の形状パラメーター	該当なし
`'Discrete Uniform'` または `'unid'`	一様分布 (離散)	`n`: 最大観測可能値	該当なし	該当なし	該当なし
`'Exponential'`	指数分布	μ: 平均値	該当なし	該当なし	該当なし
`'Extreme Value'` または `'ev'`	極値分布	μ: 位置パラメーター	σ: スケールパラメーター	該当なし	該当なし
`'Gamma'`	ガンマ分布	`a`: 形状パラメーター	`b`: スケールパラメーター	該当なし	該当なし
`'Generalized Extreme Value'` または `'gev'`	一般化極値分布	`k`: 形状パラメーター	σ: スケールパラメーター	μ: 位置パラメーター	該当なし
`'Generalized Pareto'` または `'gp'`	一般化パレート分布	`k`: テールインデックス (形状) パラメーター	σ: スケールパラメーター	該当なし	該当なし
`'Geometric'`	幾何分布	`p`: 確率パラメーター	該当なし	該当なし	該当なし
`'Half Normal'` または `'hn'`	半正規分布	σ: スケールパラメーター	該当なし	該当なし	該当なし
`'InverseGaussian'`	逆ガウス分布	μ: スケールパラメーター	λ: 形状パラメーター	該当なし	該当なし
`'Logistic'`	ロジスティック分布	μ: 平均値	σ: スケールパラメーター	該当なし	該当なし
`'LogLogistic'`	対数ロジスティック分布	μ: 対数値の平均	σ: 対数値のスケールパラメーター	該当なし	該当なし
`'LogNormal'`	対数正規分布	μ: 対数値の平均	σ: 対数値の標準偏差	該当なし	該当なし
`'Nakagami'`	仲上分布	μ: 形状パラメーター	ω: スケールパラメーター	該当なし	該当なし
`'Negative Binomial'` または `'nbin'`	負の二項分布	`r`: 成功の回数	`p`: 1 回の試行での成功の確率	該当なし	該当なし
`'Normal'`	正規分布	μ: 平均値	σ: 標準偏差	該当なし	該当なし
`'Poisson'`	ポアソン分布	λ: 平均値	該当なし	該当なし	該当なし
`'Rayleigh'`	レイリー分布	`b`: スケールパラメーター	該当なし	該当なし	該当なし
`'Rician'`	ライス分布	`s`: 非心度パラメーター	σ: スケールパラメーター	該当なし	該当なし
`'Stable'`	安定分布	α: 1 番目の形状パラメーター	β: 2 番目の形状パラメーター	γ: スケールパラメーター	δ: 位置パラメーター
`'tLocationScale'`	t 位置-スケール分布	μ: 位置パラメーター	σ: スケールパラメーター	ν: 形状パラメーター	該当なし
`'Uniform'`	一様分布 (連続)	`a`: 下限端点 (最小)	`b`: 上限端点 (最大)	該当なし	該当なし
`'Weibull'` または `'wbl'`	ワイブル分布	`a`: スケールパラメーター	`b`: 形状パラメーター	該当なし	該当なし

mle では以下の分布パラメーターは推定されません。

二項分布の試行回数。名前と値の引数 NTrials を使用してパラメーターを指定します。
半正規分布の位置パラメーター。名前と値の引数 mu を使用してパラメーターを指定します。
一般化パレート分布の位置パラメーター。名前と値の引数 theta を使用してパラメーターを指定します。

標本データが打ち切られているか、左側打ち切りまたは区間打ち切り観測値が含まれている場合、ブール分布および安定分布には名前と値の引数 Start を指定する必要があります。

例: 'Distribution','Rician'

`NTrials` — 二項分布の試行回数
スカラー | ベクトル

二項分布に対する data の対応する要素の試行回数。data と同じ行数のスカラーまたはベクトルで指定します。

この引数は、Distribution が 'Binomial' である場合 (二項分布) に必要です。

例: 'Ntrials',10

データ型: single | double

`theta` — 一般化パレート分布の位置 (しきい値) パラメーター
スカラー

一般化パレート分布の位置 (しきい値) パラメーター。スカラーとして指定します。

この引数は、Distribution が 'Generalized Pareto' である場合 (一般化パレート分布) のみ有効です。

標本データ data に非負値のみが含まれる場合、既定値は 0 です。data に負の値が含まれる場合、theta を指定しなければなりません。

例: 'theta',1

データ型: single | double

`mu` — 半正規分布の位置パラメーター
スカラー

半正規分布の位置パラメーター。スカラーを指定します。

この引数は、Distribution が 'Half Normal' である場合 (半正規分布) のみ有効です。

標本データ data に非負値のみが含まれる場合、既定値は 0 です。data に負の値が含まれる場合、mu を指定しなければなりません。

例: 'mu',1

データ型: single | double

カスタム分布を定義するオプション

すべて折りたたむ

`pdf` — カスタム確率密度関数
関数ハンドル | cell 配列

カスタム確率密度関数 (pdf)。関数ハンドルとして、または関数ハンドルおよび関数への追加の引数を含む cell 配列として指定します。

このカスタム関数は、標本データを含むベクトル、1 つ以上の個別の分布パラメーター、および cell 配列で渡される任意の追加引数を入力パラメーターとして受け入れます。この関数は確率密度値のベクトルを返します。

例: 'pdf',@newpdf

データ型: function_handle | cell

`cdf` — カスタム累積分布関数
関数ハンドル | cell 配列

カスタム累積分布関数 (cdf)。関数ハンドルとして、または関数ハンドルおよび関数への追加の引数を含む cell 配列として指定します。

このカスタム関数は、標本データを含むベクトル、1 つ以上の個別の分布パラメーター、および cell 配列で渡される任意の追加引数を入力パラメーターとして受け入れます。この関数は cdf 値のベクトルを返します。

打ち切られた観測値または切り捨てられた観測値の MLE を計算するには、cdf および pdf の両方を定義する必要があります。完全に観測された観測値および切り捨てられていない観測値の場合、mle は、cdf を使用しません。data または Censoring のいずれかを使用して打ち切り情報を指定したり、TruncationBounds を使用して打ち切りの範囲を指定したりできます。

例: 'cdf',@newcdf

データ型: function_handle | cell

`logpdf` — カスタム対数確率密度関数
関数ハンドル | cell 配列

カスタム対数確率密度関数。関数ハンドルとして、または関数ハンドルおよび関数への追加の引数を含む cell 配列として指定します。

このカスタム関数は、標本データを含むベクトル、1 つ以上の個別の分布パラメーター、および cell 配列で渡される任意の追加引数を入力パラメーターとして受け入れます。この関数は対数確率値のベクトルを返します。

例: 'logpdf',@customlogpdf

データ型: function_handle | cell

`logsf` — カスタム対数生存時間関数
関数ハンドル | cell 配列

カスタム対数生存時間関数。関数ハンドルとして、または関数ハンドルおよび関数への追加の引数を含む cell 配列として指定します。

このカスタム関数は、標本データを含むベクトル、1 つ以上の個別の分布パラメーター、および cell 配列で渡される任意の追加引数を入力パラメーターとして受け入れます。この関数は対数生存確率値のベクトルを返します。

打ち切られた観測値または切り捨てられた観測値の MLE を計算するには、logsf および logpdf の両方を定義する必要があります。完全に観測された観測値および切り捨てられていない観測値の場合、mle は、logsf を使用しません。data または Censoring のいずれかを使用して打ち切り情報を指定したり、TruncationBounds を使用して打ち切りの範囲を指定したりできます。

例: 'logsf',@logsurvival

データ型: function_handle | cell

`nloglf` — カスタムの負の対数尤度関数
関数ハンドル | cell 配列

カスタムの負の対数尤度関数。関数ハンドルとして、または関数ハンドルおよび関数への追加の引数を含む cell 配列として指定します。

このカスタム関数は、次の入力引数を表にリストされた順番で受け入れます。

カスタム関数の入力引数	説明
`params`	分布パラメーター値のベクトル。`mle` は `Start` の要素の数からパラメーターの数を検出します。
`data`	標本データ。`data` の値は、標本データのベクトル、または標本データおよび打ち切り情報からなる 2 列の行列です。
`cens`	打ち切り情報の logical ベクトル。`nloglf` は、名前と値の引数 `Censoring` を使用していない場合でも、`cens` を受け入れなければなりません。この場合、`cens` を無視するように `nloglf` を作成できます。
`freq`	データの頻度の整数ベクトル。`nloglf` は、名前と値の引数 `Frequency` を使用していない場合でも、`freq` を受け入れなければなりません。この場合、`freq` を無視するように `nloglf` を作成できます。
`trunc`	打ち切り範囲の 2 要素の数値ベクトル。`nloglf` は、名前と値の引数 `TruncationBounds` を使用している場合、`trunc` を受け入れなければなりません。

nloglf は、cell 配列で渡される追加引数を入力パラメーターとしてオプションで受け入れることができます。

nloglf はスカラーの負の対数尤度値を返し、オプションで負の対数尤度勾配ベクトル (名前と値の引数 Options の GradObj フィールドを参照) を返します。

例: 'nloglf',@negloglik

データ型: function_handle | cell

その他のオプション

すべて折りたたむ

`Censoring` — 打ち切りデータのインジケーター
0 のベクトル (既定値) | 0、–1、および 1 からなるベクトル

打ち切りデータのインジケーター。0、–1 および 1 からなるベクトルとして指定します。それぞれ完全に観測された観測値、左側打ち切り観測値、右側打ち切り観測値を示します。Censoring 値の各要素は、data の対応する観測の打ち切りステータスを示します。Censoring 値は、data と同じサイズでなければなりません。既定の設定は 0 のベクトルで、すべての観測値が完全に観測されていることを示します。

この引数を使用しても、区間打ち切り観測値は指定できません。標本データに区間打ち切り観測値が含まれる場合、2 列の行列を使用して data を指定します。mle は、data が 2 列の行列の場合に Censoring 値を無視します。

mle は、以下の組み込み分布およびカスタム分布について打ち切りをサポートします。

`Distribution` の値	分布タイプ
`'BirnbaumSaunders'`	バーンバウム・サンダース
`'Burr'`	ブール型 XII
`'Exponential'`	指数
`'Extreme Value'` または `'ev'`	極値分布
`'Gamma'`	ガンマ
`'InverseGaussian'`	逆ガウス
`'Logistic'`	ロジスティック
`'LogLogistic'`	対数ロジスティック
`'LogNormal'`	対数正規
`'Nakagami'`	仲上
`'Normal'`	正規
`'Rician'`	ライス
`'tLocationScale'`	t 位置 - スケール
`'Weibull'` または `'wbl'`	ワイブル

カスタム分布の場合、pdf と cdf、logpdf と logsf、または nloglf を使用して、分布を定義する必要があります。

mle は、打ち切りベクトルにある任意の NaN 値を無視します。さらに、data または頻度ベクトル (Frequency) に NaN 値が含まれている場合、mle は打ち切りベクトル内の対応する値を無視します。

例: 'Censoring',censored。ここで、censored は打ち切り情報を含むベクトルです。

データ型: logical | single | double

`TruncationBounds` — 打ち切り範囲
`[-Inf,Inf]` (既定値) | 2 要素のベクトル

打ち切り範囲。2 要素のベクトルを指定します。

mle は、以下の組み込み分布およびカスタム分布について切り捨てられた観測値をサポートします。

`Distribution` の値	分布タイプ
`'Beta'`	ベータ
`'BirnbaumSaunders'`	バーンバウム・サンダース
`'Burr'`	ブール
`'Exponential'`	指数
`'Extreme Value'` または `'ev'`	極値分布
`'Gamma'`	ガンマ
`'Generalized Extreme Value'` または `'gev'`	一般化極値分布
`'Generalized Pareto'` または `'gp'`	一般化パレート
`'Half Normal'` または `'hn'`	半正規
`'InverseGaussian'`	逆ガウス
`'Logistic'`	ロジスティック
`'LogLogistic'`	対数ロジスティック
`'LogNormal'`	対数正規
`'Nakagami'`	仲上
`'Normal'`	正規
`'Poisson'`	ポアソン
`'Rayleigh'`	レイリー
`'Rician'`	ライス
`'Stable'`	安定
`'tLocationScale'`	t 位置 - スケール
`'Weibull'` または `'wbl'`	ワイブル

カスタム分布の場合、pdf と cdf、logpdf と logsf、または nloglf を使用して、分布を定義する必要があります。

例: 'TruncationBounds',[0,10]

データ型: single | double

`Frequency` — 観測の頻度
1 から成るベクトル (既定値) | 非負の整数カウントのベクトル

観測の頻度。data と同じ行数をもつ非負の整数カウントのベクトルとして指定します。Frequency 値の j 番目の要素は、data の j 番目の行が観測された回数を示します。既定値は 1 のベクトルで、data の行あたり 1 回の観測を意味します。

mle は、この頻度ベクトルの NaN 値をすべて無視します。さらに、data または打ち切りベクトル (Censoring) に NaN 値が含まれている場合、mle は頻度ベクトル内の対応する値を無視します。

例: 'Frequency',freq。ここで、freq は観測頻度を含むベクトルです。

データ型: single | double

`Alpha` — 有意水準
0.05 (既定値) | 範囲 (0,1) のスカラー

パラメーター推定の信頼区間 pci の有意水準。範囲 (0,1) のスカラーを指定します。pci の信頼水準は 100(1–Alpha)% です。既定の設定では、95% の信頼区間に対して 0.05 です。

例: 'Alpha',0.01 は信頼水準を 99% として指定します。

データ型: single | double

`Options` — 反復アルゴリズムのオプション
`statset('mlecustom')` (既定値) | 構造体

反復アルゴリズムのオプション。statset によって返される構造体として指定します。

この引数を使用して、最尤最適化の詳細を制御します。この引数は以下の場合で有効です。

標本データが打ち切られている。
標本データに左側打ち切りまたは区間打ち切り観測値が含まれている。
カスタム分布を当てはめている。

関数 mle は、最適化用に次の statset オプションを解釈します。

フィールド名	説明	既定値
`GradObj`	カスタム関数 `nloglf` が 2 番目の出力として負の対数尤度の勾配ベクトルを返すことを `fmincon` が予測できるかどうかを示すフラグ。`'on'` または `'off'` を指定します。勾配を `fmincon` に指定する例については、カスタム分布当てはめ時の数値問題の回避を参照してください。 `mle` は、`fminsearch` を使用している場合、`GradObj` を無視します。名前と値の引数 `OptimFun` を使用して、最適化関数を指定できます。既定の最適化関数は `fminsearch` です。	`'off'`
`DerivStep`	相対差。`Start` と同じサイズのベクトルとして指定します。`mle` が `fmincon` を使用し、`GradObj` が `'off'` の場合に、有限差分による導関数近似で使用されます。 `mle` は、`fminsearch` を使用している場合、`DerivStep` を無視します。	`eps^(1/3)`
`FunValCheck`	分布関数から返された値の妥当性を `mle` がチェックするかどうかを示すフラグ。`'on'` または `'off'` を指定します。適切な開始点を選択しないと、適切なエラーチェックのない関数を定義した場合、分布関数は `NaN`、無限値または範囲外の値を返す可能性があります。	`'on'`
`TolBnd`	`mle` が `fmincon` を使用する場合の下限と上限のオフセット。正のスカラーを指定します。 `mle` は、厳密な不等式 (すなわち、開境界) として下限と上限を扱います。`fmincon` を使用している場合、`mle` は、`TolBnd` に指定されている下限と上限のオフセットを含めることによって範囲を近似します。	`1e-6`
`TolFun`	関数の値の終了許容誤差。正のスカラーを指定します。	`1e-6`
`TolX`	パラメーターの終了許容誤差。正のスカラーを指定します。	`1e-6`
`MaxFunEvals`	許容される関数評価の最大回数。正の整数を指定します。	`400`
`MaxIter`	許容される最大反復回数。正の整数を指定します。	`200`
`Display`	表示のレベル。`'off'`、`'final'` または `'iter'` を指定します。 `'off'` — 何の情報も表示しません。 `'final'` — 最終情報を表示します。 `'iter'` — 各反復で情報を表示します。	`'off'`

名前と値の引数 Options の例は、有限のサポートをもつ分布の MLE の計算および3 パラメーターワイブル分布を参照してください。

詳細については、fminsearch および fmincon (Optimization Toolbox) の入力引数 options を参照してください。

例: 'Options',statset('FunValCheck','off')

データ型: struct

`Start` — 初期パラメーター値
行ベクトル

ブール分布、安定分布、およびカスタム分布の初期パラメーター値。行ベクトルを指定します。Start の値の長さは、mle によって推定されるパラメーターの数と同じでなければなりません。

標本データが打ち切られているか、左側打ち切りまたは区間打ち切り観測値が含まれている場合、引数 Start がブール分布および安定分布には必要です。この引数は、カスタム分布を当てはめる場合、つまり名前と値の引数 pdf、logpdf、または nloglf を使用する場合は常に必要です。その他の場合、mle は初期値を求めるか、初期値なしで MLE を計算できます。

例: 0.05

例: [100,2]

データ型: single | double

`LowerBound` — 分布パラメーターの下限
`-Inf` のベクトル (既定値) | 行ベクトル

分布パラメーターの下限。Start と同じ長さの行ベクトルとして指定します。

この引数は以下の場合で有効です。

標本データが打ち切られている。
標本データに左側打ち切りまたは区間打ち切り観測値が含まれている。
カスタム分布を当てはめている。

例: 'Lowerbound',0

データ型: single | double

`UpperBound` — 分布パラメーターの上限
`Inf` のベクトル (既定値) | 行ベクトル

分布パラメーターの上限。Start と同じ長さの行ベクトルとして指定します。

この引数は以下の場合で有効です。

標本データが打ち切られている。
標本データに左側打ち切りまたは区間打ち切り観測値が含まれている。
カスタム分布を当てはめている。

例: 'Upperbound',1

データ型: single | double

`OptimFun` — 最適化関数
`'fminsearch'` (既定値) | `'fmincon'`

mle が尤度を最大化するために使用する最適化関数。'fminsearch' または 'fmincon' のいずれかとして指定します。'fmincon' オプションには Optimization Toolbox™ が必要です。

標本データが打ち切られている。
標本データに左側打ち切りまたは区間打ち切り観測値が含まれている。
カスタム分布を当てはめている。

例: 'Optimfun','fmincon'

出力引数

すべて折りたたむ

`phat` — パラメーター推定
行ベクトル

パラメーター推定。行ベクトルとして返されます。組み込み分布のパラメーター推定については、Distribution を参照してください。

`pci` — パラメーター推定の信頼区間
2 行 k 列の行列

パラメーター推定の信頼区間。2 行 k 列の行列として返されます。k は mle で推定されるパラメーターの数です。pci の 1 番目の行と 2 番目の行はそれぞれ、信頼限界の上限と下限を示します。

名前と値の引数 Alpha を使用して、信頼区間の有意水準を指定できます。

詳細

すべて折りたたむ

打ち切りのタイプ

mle は、左側打ち切り観測値、右側打ち切り観測値、および区間打ち切り観測値をサポートします。

時間 t での左側打ち切り観測 — 時間 t より前に発生したイベント。厳密なイベント時間は不明です。
時間 t での右側打ち切り観測 — 時間 t より後に発生したイベント。厳密なイベント時間は不明です。
区間 [t₁,t₂] 内の区間打ち切り観測 — 時間 t₁ より後かつ時間 t₂ より前に発生したイベント。厳密なイベント時間は不明です。

二重打ち切りデータには、左側打ち切り観測値および右側打ち切り観測値の両方が含まれます。

生存時間関数

生存時間関数とは、時間の関数としての生存の確率です。これは生存時間関数とも呼ばれます。

生存時間関数は、個体の生存時間が特定の値を超える確率を示します。累積分布関数 F(t) は、生存時間が特定の時点 t 以下である確率のため、連続分布の生存時間関数 S(t) は、累積分布関数の補数となります。S(t) = 1 – F(t)。

ヒント

カスタム分布関数を提供するか、左側打ち切り、二重打ち切り、区間打ち切り、または打ち切られた観測値に組み込み分布を使用すると、mle は反復最大化アルゴリズムを使用してパラメーター推定を計算します。一部のモデルやデータにおいて開始点 (Start) の選択が適切でないと、mle はグローバル最大値ではなくローカル最適値に収束したり、収束がすべて失敗する可能性があります。対数尤度がグローバル最大値近くで適切に機能する場合でも、多くの場合、アルゴリズムの収束には開始点の選択が重要です。特に、初期パラメーター値が MLE から離れている場合、分布関数のアンダーフローによって対数尤度が無制限になってしまうことがあります。

アルゴリズム

関数 mle は、負の対数尤度関数を最小化 (つまり、対数尤度関数を最大化) するか、利用できる場合は閉形式解を使用して MLE を計算します。目的関数は、分布パラメーター (θ) が与えられた場合の標本データ (X) 確率の積について対数を取り、負の値にしたものです。
$Objective Function = - \log \prod_{x \in X} P (x | θ)$
確率関数 P は、観測値ごとの打ち切り情報によって異なります。
- 完全に観測された観測 — P(x|θ) = f(x)。ここで f はパラメーター θ の確率密度関数 (pdf) です。
- 左側打ち切り観測 — P(x|θ) = F(x)。ここで F はパラメーター θ の累積分布関数 (cdf) です。
- 右側打ち切り観測 — P(x|θ) = 1 – F(x)。
- x_L と x_U の間の区間打ち切り観測 — P(x|θ) = F(x_U) – F(x_L)。
打ち切りデータの場合、mle はすべての確率が打ち切り範囲 [L,U] に含まれるように分布関数をスケーリングします。
$f_{truncation} (x) = {\begin{array}{l} \frac{f (x)}{F (U) - F (L)}, if L \leq x \leq U, \\ 0, Otherwise . \end{array}$
$F_{truncation} (x) = {\begin{array}{l} \frac{F (x) - F (L)}{F (U) - F (L)}, & if L \leq x \leq U, \\ \begin{array}{l} 0, \\ 1, \end{array} & \begin{array}{l} if x < L, \\ if x > U . \end{array} \end{array}$
関数 mle は、厳密法が使用可能であり、かつ標本データが打ち切られておらず、左側打ち切りおよび区間打ち切り観測値を含まない場合、厳密法を使用して信頼区間 pci を計算します。そうでない場合は Wald 法を使用します。厳密法が利用可能な分布は、二項分布、離散一様分布、指数分布、正規分布、対数正規分布、ポアソン分布、レイリー分布、および連続一様分布です。

拡張機能

GPU 配列
Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

使用上の注意事項および制限事項:

名前と値の引数 Distribution は 'Rician' または 'Stable' として指定できません。
名前と値の引数 pdf と cdf、logpdf と logsf、または nloglf を使用してカスタム分布を当てはめる場合、カスタム分布関数は GPU 配列をサポートする必要があります。

詳細は、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2006a より前に導入

参考

fitdist | mlecov | statset | 分布フィッター

mle

構文

説明

例

組み込み分布の MLE の計算

MLE および信頼区間の計算

カスタム確率密度関数 (pdf) の当てはめ

カスタム対数確率密度関数 (pdf) の当てはめ

カスタムな負の対数尤度関数の当てはめ

既知パラメーターによる分布の当てはめ

追加パラメーターによる分布の当てはめ

右側打ち切りデータへのカスタム分布の当てはめ

二重打ち切りデータの MLE の計算

区間打ち切りデータの MLE の計算

有限のサポートをもつ分布の MLE の計算

入力引数

data — 標本データおよび打ち切り情報 ベクトル | 2 列の行列

名前と値の引数

Distribution — 分布タイプ 'normal' (既定値) | 文字ベクトルまたは string スカラーによる分布タイプ

NTrials — 二項分布の試行回数 スカラー | ベクトル

theta — 一般化パレート分布の位置 (しきい値) パラメーター スカラー

mu — 半正規分布の位置パラメーター スカラー

pdf — カスタム確率密度関数 関数ハンドル | cell 配列

cdf — カスタム累積分布関数 関数ハンドル | cell 配列

logpdf — カスタム対数確率密度関数 関数ハンドル | cell 配列

logsf — カスタム対数生存時間関数 関数ハンドル | cell 配列

nloglf — カスタムの負の対数尤度関数 関数ハンドル | cell 配列

Censoring — 打ち切りデータのインジケーター 0 のベクトル (既定値) | 0、–1、および 1 からなるベクトル

TruncationBounds — 打ち切り範囲 [-Inf,Inf] (既定値) | 2 要素のベクトル

Frequency — 観測の頻度 1 から成るベクトル (既定値) | 非負の整数カウントのベクトル

Alpha — 有意水準 0.05 (既定値) | 範囲 (0,1) のスカラー

Options — 反復アルゴリズムのオプション statset('mlecustom') (既定値) | 構造体

Start — 初期パラメーター値 行ベクトル

LowerBound — 分布パラメーターの下限 -Inf のベクトル (既定値) | 行ベクトル

UpperBound — 分布パラメーターの上限 Inf のベクトル (既定値) | 行ベクトル

OptimFun — 最適化関数 'fminsearch' (既定値) | 'fmincon'

出力引数

phat — パラメーター推定 行ベクトル

pci — パラメーター推定の信頼区間 2 行 k 列の行列

詳細

打ち切りのタイプ

生存時間関数

ヒント

アルゴリズム

拡張機能

GPU 配列 Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

バージョン履歴

参考

トピック

`data` — 標本データおよび打ち切り情報
ベクトル | 2 列の行列

`Distribution` — 分布タイプ
`'normal'` (既定値) | 文字ベクトルまたは string スカラーによる分布タイプ

`NTrials` — 二項分布の試行回数
スカラー | ベクトル

`theta` — 一般化パレート分布の位置 (しきい値) パラメーター
スカラー

`mu` — 半正規分布の位置パラメーター
スカラー

`pdf` — カスタム確率密度関数
関数ハンドル | cell 配列

`cdf` — カスタム累積分布関数
関数ハンドル | cell 配列

`logpdf` — カスタム対数確率密度関数
関数ハンドル | cell 配列

`logsf` — カスタム対数生存時間関数
関数ハンドル | cell 配列

`nloglf` — カスタムの負の対数尤度関数
関数ハンドル | cell 配列

`Censoring` — 打ち切りデータのインジケーター
0 のベクトル (既定値) | 0、–1、および 1 からなるベクトル

`TruncationBounds` — 打ち切り範囲
`[-Inf,Inf]` (既定値) | 2 要素のベクトル

`Frequency` — 観測の頻度
1 から成るベクトル (既定値) | 非負の整数カウントのベクトル

`Alpha` — 有意水準
0.05 (既定値) | 範囲 (0,1) のスカラー

`Options` — 反復アルゴリズムのオプション
`statset('mlecustom')` (既定値) | 構造体

`Start` — 初期パラメーター値
行ベクトル

`LowerBound` — 分布パラメーターの下限
`-Inf` のベクトル (既定値) | 行ベクトル

`UpperBound` — 分布パラメーターの上限
`Inf` のベクトル (既定値) | 行ベクトル

`OptimFun` — 最適化関数
`'fminsearch'` (既定値) | `'fmincon'`

`phat` — パラメーター推定
行ベクトル

`pci` — パラメーター推定の信頼区間
2 行 k 列の行列

GPU 配列
Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。