ワイブル分布

概要

ワイブル分布は、2 パラメーターの曲線群です。この分布は、材料の破壊強度をモデル化する解析ツールとしてこの分布を提案した Waloddi Weibull にちなんで名付けられました。現在は、信頼性や寿命のモデル化に適用されています。指数分布はハザード関数が一定であるため、このような目的で使用する場合はワイブル分布のほうが指数分布よりも柔軟性があります。

Statistics and Machine Learning Toolbox™ には、ワイブル分布を処理する方法がいくつか用意されています。

確率分布を標本データに当てはめる (fitdist) かパラメーター値を指定する (makedist) ことにより、確率分布オブジェクト WeibullDistribution を作成します。そして、オブジェクト関数を使用して、分布の評価や乱数の生成などを行います。
分布フィッターアプリを使用して、ワイブル分布を対話的に処理します。オブジェクトをアプリからエクスポートしてオブジェクト関数を使用できます。
分布パラメーターを指定して、分布特有の関数 (wblcdf、wblpdf、wblinv、wbllike、wblstat、wblfit、wblrnd、wblplot) を使用します。分布特有の関数では、複数のワイブル分布についてのパラメーターを受け入れることができます。
分布名 ('Weibull') とパラメーターを指定して、汎用の分布関数 (cdf、icdf、pdf、random) を使用します。

パラメーター

Statistics and Machine Learning Toolbox の関数は、次のパラメーターをもつ 2 パラメーターのワイブル分布を使用します。

パラメーター	説明	サポート
`a`	スケール	a `> 0`
`b`	形状	b `> 0`

標準ワイブル分布は単位スケールです。

ワイブル分布では、3 番目のパラメーターを使用できます。3 パラメーターワイブル分布には位置パラメーター (2 パラメーターの場合は 0 となる) が追加されています。X がワイブル分布である場合、Y = X + c は、位置パラメーター c が追加された 3 パラメーターワイブル分布に従います。詳細については、3 パラメーターワイブル分布を参照してください。

パラメーター推定

"尤度関数" は、パラメーターの関数として見た場合の確率密度関数 (pdf) です。"最尤推定量" (MLE) は、x の値を固定した状態で尤度関数が最大になるパラメーター推定値です。ワイブル分布の a および b の最尤推定量は、連立方程式の解です。

$\begin{array}{l} \hat{a} = {[(\frac{1}{n}) \sum_{i = 1}^{n} x_{i}^{\hat{b}}]}^{\frac{1}{\hat{b}}} \\ \hat{b} = \frac{n}{(\frac{1}{\hat{a}}) \sum_{i = 1}^{n} x_{i}^{\hat{b}} \log x_{i} - \sum_{i = 1}^{n} \log x_{i}} . \end{array}$

â と $\hat{b}$ は、パラメーター a と b の不偏推定量です。

ワイブル分布をデータに当てはめてパラメーター推定値を求めるには、wblfit、fitdist、または mle を使用します。パラメーター推定を返す wblfit および mle と異なり、fitdist は当てはめた確率分布オブジェクト WeibullDistribution を返します。オブジェクトプロパティ a および b にはパラメーター推定が格納されます。

たとえば、データへのワイブル分布の当てはめとパラメーターの推定を参照してください。

確率密度関数

ワイブル分布の確率密度関数は次のようになります。

$f (x | a, b) = {\begin{array}{l} \frac{b}{a} {(\frac{x}{a})}^{b - 1} e^{- {(x / a)}^{b}} & if x \geq 0, \\ 0 & if x < 0. \end{array}$

たとえば、ワイブル分布の確率密度関数の計算を参照してください。

累積分布関数

ワイブル分布の累積分布関数 (cdf) は次のようになります。

$p = F (x | a, b) = \int_{0}^{x} b a^{- b} t^{b - 1} e^{- {(\frac{t}{a})}^{b}} d t = 1 - e^{- {(\frac{x}{a})}^{b}} .$

結果 p は、パラメーター a および b をもつワイブル分布に従う単一の観測値が区間 [0 x] に含まれる確率です。

たとえば、ワイブル分布の累積分布関数の計算を参照してください。

逆累積分布関数

ワイブル分布の逆累積分布関数は次のようになります。

$x = F^{- 1} (p | a, b) = - a {[\ln (1 - p)]}^{1 / b} .$

結果 x は、パラメーター a および b をもつワイブル分布に従う観測値が p の確率で範囲 [0 x] に含まれるような値です。

ハザード関数

ハザード関数 (瞬間故障率) は、pdf と cdf の補数との比です。f(t) と F(t) が分布の確率密度関数と累積分布関数の場合、ハザード率は $h (t) = \frac{f (t)}{1 - F (t)}$ となります。上記の f(t) と F(t) を指数分布の確率密度関数と累積分布関数で置き換えると、関数 $\frac{b}{a^{b}} x^{b - 1}$ になります。

たとえば、指数分布とワイブル分布のハザード関数の比較を参照してください。

例

データへのワイブル分布の当てはめとパラメーターの推定

ライブスクリプトを開く

スケールパラメーター 0.5、および形状パラメーター 2 をもつワイブル分布を使用して、細いフィラメントの張力強度のデータをシミュレートします。

rng('default');                  % For reproducibility
strength = wblrnd(0.5,2,100,1);  % Simulated strengths

ワイブル分布パラメーターの MLE と信頼区間を計算します。

[param,ci] = wblfit(strength)

param = 1×2

    0.4768    1.9622

ci = 2×2

    0.4291    1.6821
    0.5298    2.2890

95% の信頼区間 (0.4291,0.5298) で推定されたスケールパラメーターは 0.4768 です。

95% の信頼区間 (1.6821,2.2890) で推定された形状パラメーターは 1.9622 です。

それぞれのパラメーターの既定の信頼区間は、真の値を含んでいることがわかります。

ワイブル分布の確率密度関数の計算

ライブスクリプトを開く

スケール (A) パラメーターと形状 (B) パラメーターのさまざまな値についてワイブル分布の pdf を計算してプロットします。

x = linspace(0,30);
plot(x,wblpdf(x,10,1),'DisplayName','A=10, B=1')
hold on
plot(x,wblpdf(x,10,2),'DisplayName','A=10, B=2')
plot(x,wblpdf(x,10,4),'DisplayName','A=10, B=4')
plot(x,wblpdf(x,10,0.5),'DisplayName','A=10, B=0.5')
plot(x,wblpdf(x,10,0.25),'DisplayName','A=10, B=0.25')
plot(x,wblpdf(x,5,1),'DisplayName','A=5, B=1')
hold off
legend('show')
xlabel('x')
ylabel('pdf')

Figure contains an axes object. The axes object with xlabel x, ylabel pdf contains 6 objects of type line. These objects represent A=10, B=1, A=10, B=2, A=10, B=4, A=10, B=0.5, A=10, B=0.25, A=5, B=1.

値が B=1 の場合は、指数分布になります。値が B<1 の場合は、x が 0 に近づくにつれて密度が無限大に近づきます。値が B>1 の場合は、x が 1 に近づくにつれて密度が 0 に近づきます。

ワイブル分布の累積分布関数の計算

ライブスクリプトを開く

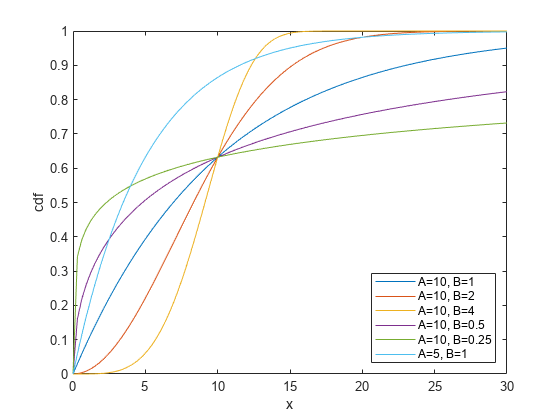
スケール (A) パラメーターと形状 (B) パラメーターのさまざまな値についてワイブル分布の cdf を計算してプロットします。

x = linspace(0,30);
plot(x,wblcdf(x,10,1),'DisplayName','A=10, B=1')
hold on
plot(x,wblcdf(x,10,2),'DisplayName','A=10, B=2')
plot(x,wblcdf(x,10,4),'DisplayName','A=10, B=4')
plot(x,wblcdf(x,10,0.5),'DisplayName','A=10, B=0.5')
plot(x,wblcdf(x,10,0.25),'DisplayName','A=10, B=0.25')
plot(x,wblcdf(x,5,1),'DisplayName','A=5, B=1')
hold off
legend('show','Location','southeast')
xlabel('x')
ylabel('cdf')

Figure contains an axes object. The axes object with xlabel x, ylabel cdf contains 6 objects of type line. These objects represent A=10, B=1, A=10, B=2, A=10, B=4, A=10, B=0.5, A=10, B=0.25, A=5, B=1.

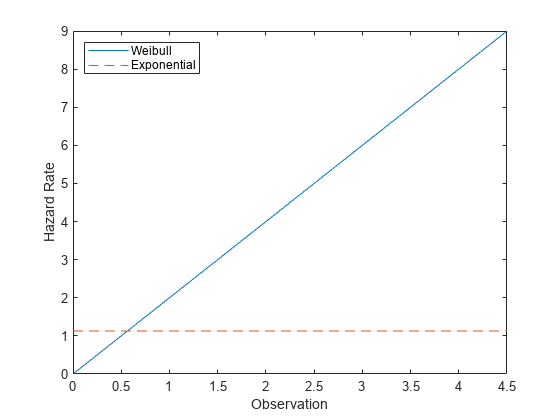
指数分布とワイブル分布のハザード関数の比較

ライブスクリプトを開く

指数分布では定数のハザード関数ですが、ワイブル分布ではこれは一般的ではありません。この例では、ワイブルハザード率は年数と共に増加しています (これは妥当な想定です)。

スケールパラメーター 1、および形状パラメーター 2 をもつワイブル分布のハザード関数を計算します。

t = 0:0.1:4.5;
h1 = wblpdf(t,1,2)./(1-wblcdf(t,1,2));

スケールパラメーター 1、および形状パラメーター 2 をもつワイブル分布の平均を計算します。

mu = wblstat(1,2)

mu = 
0.8862

平均 mu をもつ指数分布のハザード関数を計算します。

h2 = exppdf(t,mu)./(1-expcdf(t,mu));

両方のハザード関数を同じ軸上にプロットします。

plot(t,h1,'-',t,h2,'--')
xlabel('Observation')
ylabel('Hazard Rate')
legend('Weibull','Exponential','location','northwest')

Figure contains an axes object. The axes object with xlabel Observation, ylabel Hazard Rate contains 2 objects of type line. These objects represent Weibull, Exponential.

参照

[1] Crowder, Martin J., ed. Statistical Analysis of Reliability Data. Reprinted. London: Chapman & Hall, 1995.

[2] Devroye, Luc. Non-Uniform Random Variate Generation. New York, NY: Springer New York, 1986. https://doi.org/10.1007/978-1-4613-8643-8

[3] Forbes, Catherine, Merran Evans, Nicholas Hastings, and Brian Peacock. Statistical Distributions. 4th ed. Wiley, 2010.

[4] Lawless, Jerald F. Statistical Models and Methods for Lifetime Data. 2nd ed. Wiley Series in Probability and Statistics. Hoboken, N.J: Wiley-Interscience, 2003.

[5] Meeker, William Q., and Luis A. Escobar. Statistical Methods for Reliability Data. Wiley Series in Probability and Statistics. Applied Probability and Statistics Section. New York: Wiley, 1998.

参考