指数分布
概要
指数分布は、1 パラメーターの曲線群です。指数分布は、過去の待ち時間と未来の待ち時間が独立であるときの待ち時間をモデル化します。たとえば、電球が次の使用時間内に、故障してしまう確率は、今までに何分間使用したかということとは相対的に独立しています。
Statistics and Machine Learning Toolbox™ には、指数分布を処理する方法がいくつか用意されています。
確率分布を標本データに当てはめる (
fitdist) かパラメーター値を指定する (makedist) ことにより、確率分布オブジェクトExponentialDistributionを作成します。そして、オブジェクト関数を使用して、分布の評価や乱数の生成などを行います。分布フィッター アプリを使用して、指数分布を対話的に処理します。オブジェクトをアプリからエクスポートしてオブジェクト関数を使用できます。
分布パラメーターを指定して、分布特有の関数 (
expcdf、exppdf、expinv、explike、expstat、expfit、exprnd) を使用します。分布特有の関数では、複数の指数分布についてのパラメーターを受け入れることができます。分布名 (
'Exponential') とパラメーターを指定して、汎用の分布関数 (cdf、icdf、pdf、random) を使用します。
パラメーター
指数分布は、次のパラメーターを使用します。
| パラメーター | 説明 | サポート |
|---|---|---|
mu (μ) | 平均 | μ > 0 |
パラメーター μ は、指数分布の標準偏差とも等しくなります。
標準指数分布では、μ=1 です。
指数分布をパラメーター化する一般的な代替手段は、事象が発生するまでの平均待ち時間 μ を使用する代わりに、ある区間の平均事象数として定義された λ を使用することです。λ と μ は互いに逆数の関係にあります。
パラメーター推定
"尤度関数" は、パラメーターの関数として見た場合の確率密度関数 (pdf) です。"最尤推定量" (MLE) は、x の値を固定した状態で尤度関数が最大になるパラメーター推定値です。
指数分布の μ の最尤推定量は、 です。ここで、 は、標本 x1, x2, …, xn の標本平均です。標本平均は、パラメーター μ の不偏推定量です。
指数分布をデータに当てはめてパラメーター推定値を求めるには、expfit、fitdist または mle を使用します。パラメーター推定を返す expfit および mle と異なり、fitdist は当てはめた確率分布オブジェクト ExponentialDistribution を返します。オブジェクト プロパティ mu には、パラメーター推定が格納されます。
たとえば、データへの指数分布の当てはめを参照してください。
確率密度関数
指数分布の確率密度関数は次のようになります。
たとえば、指数分布の確率密度関数の計算を参照してください。
累積分布関数
指数分布の累積分布関数 (cdf) は次のようになります。
結果 p は、平均 μ をもつ指数分布に従う単一の観測値が区間 [0, x] に含まれる確率です。
たとえば、指数分布の累積分布関数の計算を参照してください。
逆累積分布関数
指数分布の逆累積分布関数 (icdf) は次のようになります。
結果 x は、パラメーター μ をもつ指数分布に従う観測値が p の確率で範囲 [0 x] に含まれるような値です。
ハザード関数
ハザード関数 (瞬間故障率) は、pdf と cdf の補数との比です。f(t) と F(t) が、それぞれ分布の確率密度関数と累積分布関数の場合、ハザード率は で表されます。f(t) と F(t) を指数分布の確率密度関数と累積分布関数で置き換えると、定数 λ になります。指数分布は、ハザード関数が一定である唯一の連続分布です。λ は μ の逆数で、特定の時間間隔において事象が発生する割合と解釈できます。したがって、生存時間をモデル化した場合、ある個体がさらに単位時間生き残る確率は、個体の現在の年齢とは無関係となります。
たとえば、指数分布した寿命を参照してください。
例
データへの指数分布の当てはめ
平均 700 をもつ指数分布に従う 100 個の乱数の標本を生成します。
x = exprnd(700,100,1); % Generate samplefitdist を使用して指数分布をデータに当てはめます。
pd = fitdist(x,'exponential')pd =
ExponentialDistribution
Exponential distribution
mu = 641.934 [532.598, 788.966]
fitdist は、ExponentialDistribution オブジェクトを返します。パラメーター推定値の横にある区間は、分布パラメーターの 95% 信頼区間です。
分布関数を使用してパラメーターを推定します。
[muhat,muci] = expfit(x) % Distribution specific functionmuhat = 641.9342
muci = 2×1
532.5976
788.9660
[muhat2,muci2] = mle(x,'distribution','exponential') % Generic distribution function
muhat2 = 641.9342
muci2 = 2×1
532.5976
788.9660
指数分布の確率密度関数の計算
パラメーター mu = 2 を使用して指数分布の確率密度関数を計算します。
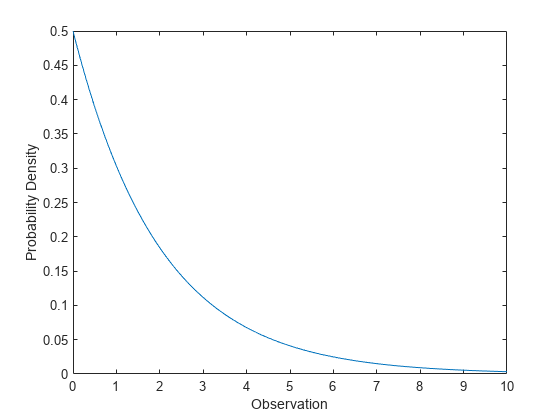
x = 0:0.1:10; y = exppdf(x,2);
確率密度関数をプロットします。
figure; plot(x,y) xlabel('Observation') ylabel('Probability Density')
指数分布の累積分布関数の計算
パラメーター mu = 2 を使用して指数分布の累積分布関数を計算します。
x = 0:0.1:10; y = expcdf(x,2);
累積分布関数をプロットします。
figure; plot(x,y) xlabel('Observation') ylabel('Cumulative Probability')

指数分布した寿命
値 1 ~ 5 での、平均 mu = 2 をもつ指数分布のハザード関数を計算します。
x = 1:5; lambda1 = exppdf(x,2)./(1-expcdf(x,2))
lambda1 = 1×5
0.5000 0.5000 0.5000 0.5000 0.5000
指数分布のハザード関数 (生存に対する瞬間故障率) は定数で、常に 1/mu になります。この定数は、多くの場合 λ で表されます。
x = 3 での、平均 1 ~ 5 をもつ指数分布のハザード関数を評価します。
mu = 1:5; lambda2 = exppdf(3,mu)./(1-expcdf(3,mu))
lambda2 = 1×5
1.0000 0.5000 0.3333 0.2500 0.2000
指数分布に従う寿命をもつ個体がさらに 1 単位時間生き残る確率は、その個体がこれまで生き残ってきた時間とは無関係です。
平均生存時間が 10 年である場合に、さまざまな年齢の個体がさらに 1 年生存する確率を計算します。
x2 = 5:5:25; x3 = x2 + 1; deltap = (expcdf(x3,10)-expcdf(x2,10))./(1-expcdf(x2,10))
deltap = 1×5
0.0952 0.0952 0.0952 0.0952 0.0952
ある個体がさらに 1 年生存する確率は、その個体がこれまで生き残ってきた時間とは関係なく同じになります。
関連する分布
ブール型 XII 分布 — ブール分布は、3 パラメーターの連続分布です。指数分布とガンマ分布をその平均について複合させると、ブール分布が得られます。
ガンマ分布 — ガンマ分布は、2 パラメーターの連続分布です。a (形状) および b (スケール) のパラメーターをもちます。a = 1 のとき、ガンマ分布は平均 μ = b をもつ指数分布と等しくなります。平均 μ をもつ指数分布に従う k 個の確率変数の和は、a = k および μ = b のパラメーターをもつガンマ分布に従います。
幾何分布 — 幾何分布は、1 パラメーターの離散分布です。ベルヌーイ試行を繰り返したときに最初に成功するまでの総失敗回数をモデル化します。幾何分布は指数分布の離散版で、ハザード関数が一定である唯一の離散分布です。
一般化パレート分布 — 一般化パレート分布は、3 パラメーターの連続分布です。k (形状)、σ (スケール)、および θ (しきい値) のパラメーターをもちます。k = 0 かつ θ = 0 のとき、一般化パレート分布は平均 μ = σ をもつ指数分布と等しくなります。
ポアソン分布— ポアソン分布は、非負の整数値をとる 1 パラメーターの離散分布です。パラメーター λ は、分布の平均と分散の両方を示します。ポアソン分布は、特定の期間において無作為に起こる事象の回数のカウントをモデル化します。このようなモデルでは、事象の発生間隔は平均 をもつ指数分布によってモデル化されます。
ワイブル分布 — ワイブル分布は、2 パラメーターの連続分布です。a (スケール) および b (形状) のパラメーターをもちます。ワイブル分布は寿命のモデル化にも使用されますが、ハザード率は一定ではありません。b = 1 のとき、ワイブル分布は平均 μ = a をもつ指数分布と等しくなります。
たとえば、指数分布とワイブル分布のハザード関数の比較を参照してください。
参照
[1] Crowder, Martin J., ed. Statistical Analysis of Reliability Data. Reprinted. London: Chapman & Hall, 1995.
[2] Kotz, Samuel, and Saralees Nadarajah. Extreme Value Distributions: Theory and Applications. London : River Edge, NJ: Imperial College Press; Distributed by World Scientific, 2000.
[3] Meeker, William Q., and Luis A. Escobar. Statistical Methods for Reliability Data. Wiley Series in Probability and Statistics. Applied Probability and Statistics Section. New York: Wiley, 1998.
[4] Lawless, Jerald F. Statistical Models and Methods for Lifetime Data. 2nd ed. Wiley Series in Probability and Statistics. Hoboken, N.J: Wiley-Interscience, 2003.
参考
ExponentialDistribution | expcdf | exppdf | expinv | explike | expstat | expfit | exprnd | makedist | fitdist