幾何分布
概要
幾何分布は、1 パラメーターの曲線群です。それぞれの試行の結果が成功か失敗のどちらかである一連の独立試行において、1 回成功するまでの失敗回数をモデル化します。各試行の成功確率は定数です。たとえばコインを投げる場合について、幾何分布では、表が出るまで裏が観測され続ける回数をモデル化します。幾何分布は離散で、非負整数にのみ存在します。
Statistics and Machine Learning Toolbox™ には、幾何分布を処理する方法がいくつか用意されています。
パラメーター
幾何分布は、次のパラメーターを使用します。
| パラメーター | 説明 | サポート |
|---|---|---|
p | 成功確率 |
確率密度関数
幾何分布の確率密度関数 (pdf) は次のようになります。
p は成功の確率で、x は最初に成功するまでに失敗した回数です。結果の y は、任意の試行の成功確率が p のときに、成功するまでに x 回の試行を正確に観測する確率です。離散分布では、pdf は確率質量関数 (pmf) とも呼ばれます。
たとえば、幾何分布 pdf の計算を参照してください。
累積分布関数
幾何分布の cdf (累積分布関数) は次のようになります。
p は成功の確率で、x は最初に成功するまでに失敗した回数です。結果 y は、任意の試行の成功確率が p のときに、成功するまでに最大 x 回の試行を観測する確率です。
たとえば、幾何分布の cdf の計算を参照してください。
記述統計
幾何分布の平均は 、幾何分布の分散は です。ここで、p は成功確率です。
ハザード関数
ハザード関数 (瞬間故障率) は、pdf と cdf の補数との比です。f(t) と F(t) が、それぞれ分布の確率密度関数と累積分布関数の場合、ハザード率は で表されます。上記の f(t) と F(t) を幾何分布の確率密度関数と累積分布関数で置き換えると、平均の逆数に等しい定数になります。幾何分布はハザード関数が一定である唯一の離散分布です。したがって、成功が観測される確率は、これまで観測された失敗の数とは無関係となります。
例
幾何分布 pdf の計算
成功確率が 0.25 である幾何分布の pdf を計算します。
x = 0:20; y = geopdf(x,0.25);
幅が 1 のバーで pdf をプロットします。
figure bar(x,y,1) xlabel('Observation') ylabel('Probability')
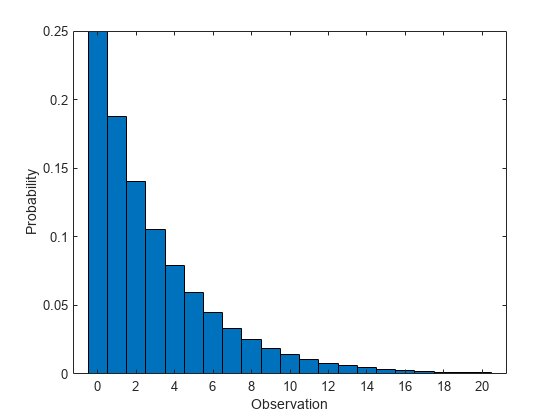
幾何分布の cdf の計算
成功確率が 0.25 である幾何分布の cdf を計算します。
x = 0:20; y = geocdf(x,0.25);
累積分布関数をプロットします。
figure stairs(x,y) xlabel('Observation') ylabel('Cumulative Probability')

幾何分布の確率の計算
使用期間が 5 年の自動車のバッテリーが、寒い気候で機能しない確率は 0.03 であると仮定します。ドライバーは、寒い気候が 25 日続く間、自動車のエンジンを毎朝始動しようと試みます。このシナリオを幾何分布を使用してモデル化します。この場合、観測する事象は、自動車のエンジンが始動しないという事象です。
25 に対する cdf を計算し、25 日間のいずれかの日に自動車のエンジンが始動しない確率を求めます。
x = 25; p = 0.03; notstart = geocdf(x,p)
notstart = 0.5470
補数を計算し、自動車のエンジンが 25 日間毎日始動する確率を求めます。
start = 1 - notstart
start = 0.4530
関連する分布
参照
[1] Abramowitz, Milton, and Irene A. Stegun, eds. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. 9. Dover print.; [Nachdr. der Ausg. von 1972]. Dover Books on Mathematics. New York, NY: Dover Publ, 2013.
[2] Devroye, Luc. Non-Uniform Random Variate Generation. New York, NY: Springer New York, 1986. https://doi.org/10.1007/978-1-4613-8643-8
[3] Evans, Merran, Nicholas Hastings, and Brian Peacock. Statistical Distributions. 2nd ed. New York: J. Wiley, 1993.
参考
geocdf | geopdf | geoinv | geostat | geornd | NegativeBinomialDistribution