ポアソン分布
概要
ポアソン分布は、1 パラメーターの曲線群です。無作為に起こる事象の回数をモデル化します。この分布は、特定の量の時間、距離、面積などにおいて無作為に起こる事象の回数を数える場合に適しています。ポアソン分布を適用する例として、ガイガー カウンターから 1 秒間に出る音の数、1 時間に店に入ってくる人の数、1 分間にネットワーク上で失われるパケットの数などがあります。
Statistics and Machine Learning Toolbox™ には、ポアソン分布を処理する方法がいくつか用意されています。
確率分布を標本データに当てはめるかパラメーター値を指定することにより、確率分布オブジェクト
PoissonDistributionを作成します。そして、オブジェクト関数を使用して、分布の評価や乱数の生成などを行います。分布フィッター アプリを使用して、ポアソン分布を対話的に処理します。オブジェクトをアプリからエクスポートしてオブジェクト関数を使用できます。
分布パラメーターを指定して、分布特有の関数 (
poisscdf、poisspdf、poissinv、poisstat、poissfit、poissrnd) を使用します。分布特有の関数では、複数のポアソン分布についてのパラメーターを受け入れることができます。分布名 (
'Poisson') とパラメーターを指定して、汎用の分布関数 (cdf、icdf、pdf、random) を使用します。
パラメーター
ポアソン分布は、次のパラメーターを使用します。
| パラメーター | 説明 | サポート |
|---|---|---|
lambda (λ) | 平均 |
パラメーター λ は、ポアソン分布の分散とも等しくなります。
パラメーターが λ1 および λ2 である 2 つのポアソン確率変数の和は、パラメーターが λ = λ1 + λ2 であるポアソン確率変数になります。
確率密度関数
ポアソン分布の確率密度関数 (pdf) は次のようになります。
この結果は、無作為に起こる事象がちょうど x 回発生する確率です。離散分布では、pdf は確率質量関数 (pmf) とも呼ばれます。
たとえば、ポアソン分布の確率密度関数の計算を参照してください。
累積分布関数
ポアソン分布の累積分布関数 (cdf) は次のようになります。
この結果は、無作為に起こる事象が最大 x 回発生する確率です。
たとえば、ポアソン分布の累積分布関数の計算を参照してください。
例
ポアソン分布の確率密度関数の計算
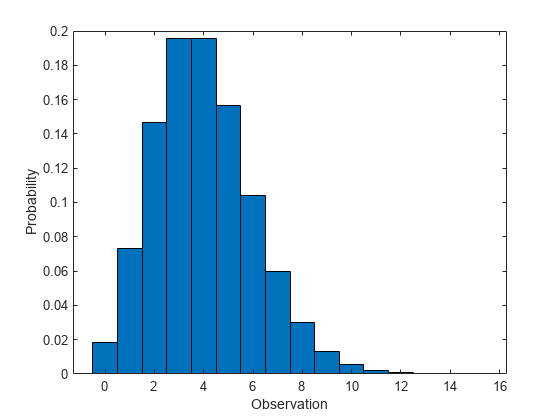
パラメーター lambda = 4 を使用してポアソン分布の pdf を計算します。
x = 0:15; y = poisspdf(x,4);
幅が 1 のバーで pdf をプロットします。
figure bar(x,y,1) xlabel('Observation') ylabel('Probability')
ポアソン分布の累積分布関数の計算
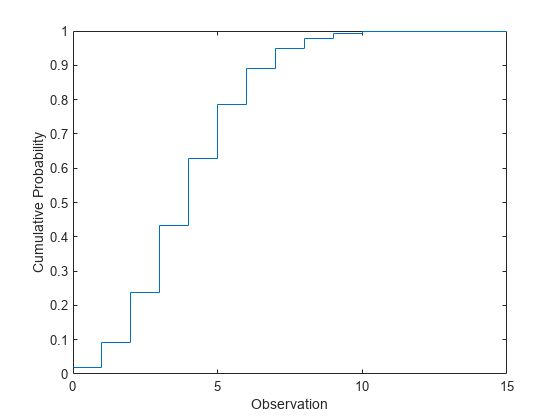
パラメーター lambda = 4 を使用してポアソン分布の cdf を計算します。
x = 0:15; y = poisscdf(x,4);
累積分布関数をプロットします。
figure stairs(x,y) xlabel('Observation') ylabel('Cumulative Probability')
ポアソン分布と正規分布の pdf の比較
lambda が大きい場合、ポアソン分布は平均 lambda と分散 lambda をもつ正規分布で近似できます。
パラメーター lambda = 50 を使用してポアソン分布の pdf を計算します。
lambda = 50; x1 = 0:100; y1 = poisspdf(x1,lambda);
対応する正規分布の pdf を計算します。
mu = lambda; sigma = sqrt(lambda); x2 = 0:0.1:100; y2 = normpdf(x2,mu,sigma);
同じ軸に pdf をプロットします。
figure bar(x1,y1,1) hold on plot(x2,y2,'LineWidth',2) xlabel('Observation') ylabel('Probability') title('Poisson and Normal pdfs') legend('Poisson Distribution','Normal Distribution','location','northwest') hold off
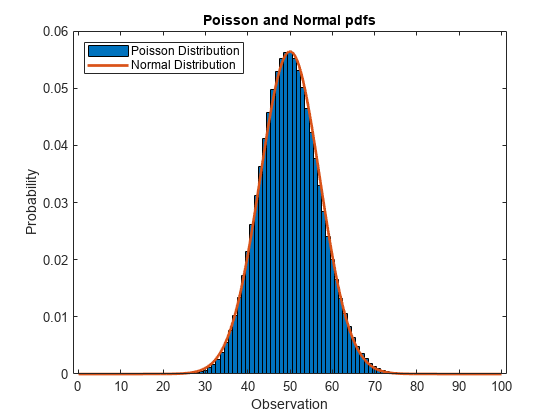
正規分布の pdf はポアソン分布の pdf に近づきます。
関連する分布
二項分布 — 二項分布は、2 パラメーターの離散分布です。成功確率が p である独立試行を N 回行ったときの成功回数をカウントします。ポアソン分布は、Np = λ としたときに N を無限大、p をゼロに近づけた二項分布の限定的なケースです。二項分布とポアソン分布の pdf の比較を参照してください。
指数分布 — 指数分布は、1 パラメーターの連続分布です。μ (平均) のパラメーターをもちます。ポアソン分布は、特定の期間において無作為に起こる事象の回数のカウントをモデル化します。このようなモデルでは、事象の発生間隔は平均 をもつ指数分布によってモデル化されます。
正規分布 — 正規分布は、2 パラメーターの連続分布です。μ (平均) および σ (標準偏差) のパラメーターをもちます。λ が大きい場合、ポアソン分布は μ = λ かつ σ2 = λ である正規分布で近似できます。ポアソン分布と正規分布の pdf の比較を参照してください。
参照
[1] Abramowitz, Milton, and Irene A. Stegun, eds. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. 9. Dover print.; [Nachdr. der Ausg. von 1972]. Dover Books on Mathematics. New York, NY: Dover Publ, 2013.
[2] Devroye, Luc. Non-Uniform Random Variate Generation. New York, NY: Springer New York, 1986. https://doi.org/10.1007/978-1-4613-8643-8
[3] Evans, Merran, Nicholas Hastings, and Brian Peacock. Statistical Distributions. 2nd ed. New York: J. Wiley, 1993.
[4] Loader, Catherine. Fast and Accurate Computation of Binomial Probabilities. July 9, 2000.
参考
PoissonDistribution | poisscdf | poisspdf | poissinv | poisstat | poissfit | poissrnd