二項分布

概要

二項分布は、2 パラメーターの曲線群です。二項分布は、同じ成功確率をもつ独立試行をある決まった回数行ったときの総成功回数をモデル化するのに使用されます。たとえば、歪みのない硬貨を 10 回投げたときに所定の回数だけ表が出る確率をモデル化するのに使用されます。

Statistics and Machine Learning Toolbox™ には、二項分布を処理する方法がいくつか用意されています。

• 確率分布を標本データに当てはめる (fitdist) かパラメーター値を指定する (makedist) ことにより、確率分布オブジェクト BinomialDistribution を作成します。そして、オブジェクト関数を使用して、分布の評価や乱数の生成などを行います。

• 分布フィッター アプリを使用して、二項分布を対話的に処理します。オブジェクトをアプリからエクスポートしてオブジェクト関数を使用できます。

• 分布パラメーターを指定して、分布特有の関数 (binocdf、binopdf、binoinv、binostat、binofit、binornd) を使用します。分布特有の関数では、複数の二項分布についてのパラメーターを受け入れることができます。

• 分布名 ('Binomial') とパラメーターを指定して、汎用の分布関数 (cdf、icdf、pdf、random) を使用します。

パラメーター

二項分布は、次のパラメーターを使用します。

パラメーター	説明	サポート
N	試行回数	正の整数
p	1 回の試行における成功確率	$$0\le p\le 1$$

同じパラメーター p をもつ 2 つの二項確率変数の和も、試行回数の和に等しい N をもつ二項確率変数です。

確率密度関数

二項分布の確率密度関数 (pdf) は次のようになります。

$$f\left(x|N,p\right)=\left(\begin{array}{c}N\\ x\end{array}\right)p^x{\left(1-p\right)}^{N-x};x=0,1,2,\mathrm{...},N,$$

ここで x は、成功確率が p であるベルヌーイ過程を N 回試行した場合の成功数です。この結果は、N 回の試行で正確に x 回成功する確率です。離散分布では、pdf は確率質量関数 (pmf) とも呼ばれます。

たとえば、二項分布の確率密度関数の計算を参照してください。

累積分布関数

二項分布の累積分布関数 (cdf) は次のようになります。

$$F\left(x|N,p\right)={\displaystyle \sum _{i=0}^x\left(\begin{array}{c}N\\ i\end{array}\right)p^i{\left(1-p\right)}^{N-i}};x=0,1,2,\mathrm{...},N,$$

ここで x は、成功確率が p であるベルヌーイ過程を N 回試行した場合の成功数です。この結果は、N 回の試行で最大 x 回成功する確率です。

たとえば、二項分布の累積分布関数の計算を参照してください。

記述統計

二項分布の平均は Np です。

二項分布の分散は Np(1 – p) です。

例

データへの二項分布の当てはめ

1 回の成功確率が 0.9 である試行を 100 回行ったときの成功回数をカウントする二項乱数を生成します。

x = binornd(100,0.9)

x = 85

fitdist を使用して二項分布をデータに当てはめます。

pd = fitdist(x,'Binomial','NTrials',100)

pd = 
  BinomialDistribution

  Binomial distribution
    N =  100
    p = 0.85   [0.764692, 0.913546]

fitdist は、BinomialDistribution オブジェクトを返します。p の横にある区間は、p を推定する 95% 信頼区間です。

分布関数を使用してパラメーター p を推定します。

[phat,pci] = binofit(x,100) % Distribution-specific function

phat = 0.8500

pci = 1×2

    0.7647    0.9135

[phat2,pci2] = mle(x,'distribution','Binomial',"NTrials",100) % Generic distribution function

phat2 = 0.8500

pci2 = 2×1

    0.7647
    0.9135

二項分布の確率密度関数の計算

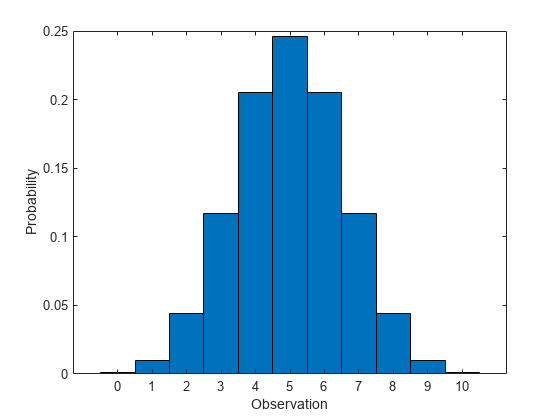
試行回数 10、成功確率 0.5 の二項分布の pdf を計算します。

x = 0:10;
y = binopdf(x,10,0.5);

幅が 1 のバーで pdf をプロットします。

figure
bar(x,y,1)
xlabel('Observation')
ylabel('Probability')

二項分布の累積分布関数の計算

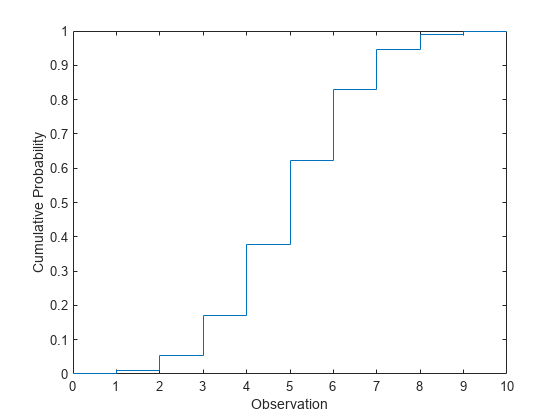
試行回数 10、成功確率 0.5 の二項分布の cdf を計算します。

x = 0:10;
y = binocdf(x,10,0.5);

累積分布関数をプロットします。

figure
stairs(x,y)
xlabel('Observation')
ylabel('Cumulative Probability')

二項分布と正規分布の pdf の比較

N が大きく、p が大きすぎも小さすぎもしない場合、パラメーター N と p をもつ二項分布は、平均 N*p と分散 N*p*(1–p) をもつ正規分布で近似できます。

1 回の成功確率が 0.6 である試行を 50 回行ったときの成功回数をカウントする二項分布の pdf を計算します。

N = 50;
p = 0.6;
x1 = 0:N;
y1 = binopdf(x1,N,p);

対応する正規分布の pdf を計算します。

mu = N*p;
sigma = sqrt(N*p*(1-p));
x2 = 0:0.1:N;
y2 = normpdf(x2,mu,sigma);

同じ軸に pdf をプロットします。

figure
bar(x1,y1,1)
hold on
plot(x2,y2,'LineWidth',2)
xlabel('Observation')
ylabel('Probability')
title('Binomial and Normal pdfs')
legend('Binomial Distribution','Normal Distribution','location','northwest')
hold off

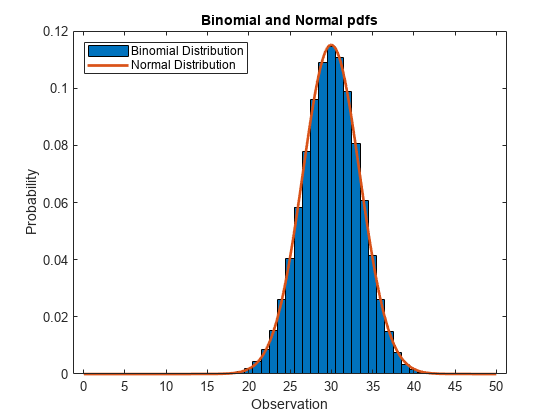
正規分布の pdf は二項分布の pdf に近づきます。

二項分布とポアソン分布の pdf の比較

p が小さく、N*p も小さい場合、パラメーター N と p をもつ二項分布は、平均 N*p をもつポアソン分布で近似できます。

1 回の成功確率が 0.05 である試行を 20 回行ったときの成功回数をカウントする二項分布の pdf を計算します。

N = 20;
p = 0.05;
x = 0:N;
y1 = binopdf(x,N,p);

対応するポアソン分布の pdf を計算します。

mu = N*p;
y2 = poisspdf(x,mu);

同じ軸に pdf をプロットします。

figure
bar(x,[y1; y2])
xlabel('Observation')
ylabel('Probability')
title('Binomial and Poisson pdfs')
legend('Binomial Distribution','Poisson Distribution','location','northeast')

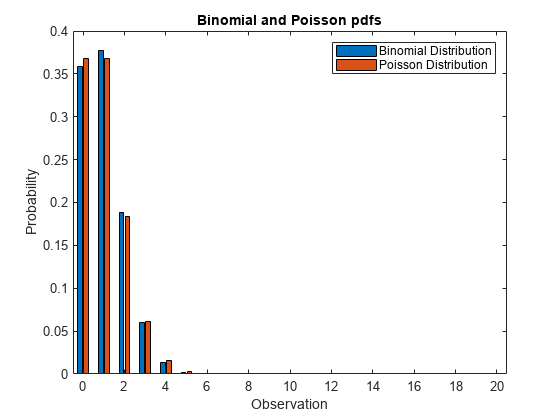
ポアソン分布の pdf は二項分布の pdf に近づきます。

関連する分布

• ベルヌーイ分布 — ベルヌーイ分布は、1 パラメーターの離散分布です。N = 1 の二項分布として発生する単一の試行の成功確率をモデル化します。

• 多項分布 — 多項分布は、各試行の潜在的な結果が 2 つより多い場合の二項分布を一般化した離散分布です。

• 正規分布 — 正規分布は、2 パラメーターの連続分布です。μ (平均) および σ (標準偏差) のパラメーターをもちます。N が大きくなると、µ = Np および σ² = Np(1 – p) である正規分布で二項分布を近似できます。二項分布と正規分布の pdf の比較を参照してください。

• ポアソン分布— ポアソン分布は、非負の整数値をとる 1 パラメーターの離散分布です。パラメーター λ は、分布の平均と分散の両方を示します。ポアソン分布は、Np = λ としたときに N を無限大、p をゼロに近づけた二項分布の限定的なケースです。二項分布とポアソン分布の pdf の比較を参照してください。

参照

[1] Abramowitz, Milton, and Irene A. Stegun, eds. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. 9. Dover print.; [Nachdr. der Ausg. von 1972]. Dover Books on Mathematics. New York, NY: Dover Publ, 2013.

[2] Evans, Merran, Nicholas Hastings, and Brian Peacock. Statistical Distributions. 2nd ed. New York: J. Wiley, 1993.

[3] Loader, Catherine. Fast and Accurate Computation of Binomial Probabilities. July 9, 2000.

参考

BinomialDistribution | binocdf | binopdf | binoinv | binostat | binofit | binornd | makedist | fitdist

関連するトピック

• ベルヌーイ分布
• 確率分布の操作
• サポートされている分布