ブール型 XII 分布

定義

ブール型 XII 分布は、正の実数直線上の分布の 3 パラメーター群です。ブール分布の累積分布関数 (cdf) は次のようになります。

$$F(x|\alpha ,c,k)=1-\frac{1}{{\left(1+{\left(\frac{x}{\alpha }\right)}^c\right)}^k},x>0,\alpha >0,c>0,k>0,$$

ここで、c と k は形状パラメーター、α はスケール パラメーターです。確率密度関数 (pdf) は次のようになります。

$$f(x|\alpha ,c,k)=\frac{\frac{kc}{\alpha }{\left(\frac{x}{\alpha }\right)}^{c-1}}{{\left(1+{\left(\frac{x}{\alpha }\right)}^c\right)}^{k+1}},x>0,\alpha >0,c>0,k>0.$$

ブール型 XII 分布の密度は、c ≤ 1 の場合は L 形に、それ以外の場合は単峰形になります。

背景

ブール分布は 1942 年にブール氏により 2 パラメーター群として最初に考察されました。その後 1980 年にタジカマラ氏によって追加のスケール パラメーターが導入されています。これは柔軟な分布族であり、多岐にわたる分布形状を表現することができます。ブール分布は、限定的なケースでは、一般的に使用される次のような分布と重複が含まれています。ガンマ、対数正規、対数ロジスティック、釣り鐘形、J 形ベータの各分布 (ただし、U 形分布は含まれません)。一部の複合分布もブール分布に対応します。たとえば、ワイブル分布とガンマ分布をそのスケール パラメーターに対して複合させると、その結果としてブール分布が得られます。同様に、指数分布とガンマ分布をそのレート パラメーター 1/μ について複合させた場合にもブール分布が得られます。また、ブール分布には 2 つの漸近的な限定ケースもあります。ワイブルおよびパレート タイプ I です。

ブール分布は広範な実測データを近似できます。分布のパラメーターの異なる値によって、広範囲の歪度と尖度のセットをカバーできます。したがって、金融、水文学、信頼度など、さまざまな分野の各種データのモデル化に使用されています。ブール分布を使ってモデル化されるデータの例には、世帯収入、穀物価格、保険リスク、移動時間、洪水位、故障データなどがあります。

ブール型 XII 分布の生存時間関数とハザード関数は、それぞれ次のようになります。

$$S\left(x|\alpha ,c,k\right)=\frac{1}{{\left[1+{\left(\frac{x}{\alpha }\right)}^c\right]}^k}$$

および

$$h\left(x|\alpha ,c,k\right)=\frac{\frac{kc}{\alpha }{\left(\frac{x}{\alpha }\right)}^{c-1}}{1+{\left(\frac{x}{\alpha }\right)}^c}.$$

c > 1 である場合、ハザード関数 h(x) は、最頻値が x = α(c – 1)^1/c の非単調になります。

パラメーター

3 パラメーターのブール分布は、そのスケール パラメーター α と形状パラメーター c および k によって定義されます。mle または fitdist を使用してパラメーターを推定できます。どちらの関数もブール分布について打ち切りデータをサポートします。

スケール パラメーターを 0.5、形状パラメーターを 2 と 5 に設定したブール分布から標本データを生成します。

rng('default')
R = random('burr',0.5,2,5,1000,1);

パラメーターと信頼区間を推定します。

[phat,pci] = mle(R,'distribution','burr')

phat =

    0.4154    2.1217    4.0550


pci =

    0.2985    1.9560    2.4079
    0.5782    2.3014    6.8288

パラメーターの既定の 95% 信頼区間は、真のパラメーター値を含んでいます。

3 パラメーターのブール分布は、そのパラメーターが発散するにつれてその 2 つの限定的な形状のいずれかに漸近的に収束します。

• k→0、c→∞、ck = λ の場合、ブール分布は 2 パラメーターのパレート分布に縮小し、cdf は次のようになります。

  $$F_P=1-{\left(\frac{x}{\alpha }\right)}^{-\lambda },x\ge \alpha .$$

• k→∞、α→∞、α/k^1/c = θ の場合、ブール分布は 2 パラメーターのワイブル分布に縮小し、cdf は次のようになります。

  $$F_W(x|c,\theta )=1-\exp \left[-{\left(\frac{x}{\theta }\right)}^c\right].$$

mle または fitdist がこのようなダイバージェンスを検出した場合、エラー メッセージが返されますが、極限分布およびその分布の対応するパラメーター推定についての情報が提供されます。

ブール分布の近似と cdf の算出

この例では、ブール分布をデータに近似させ、cdf を求めてブール分布近似のヒストグラムを作成する方法を示します。

1.標本データを読み込みます。

load arrhythmia

X の 5 列目には、心電図から取得した QRS 持続時間という測定データが含まれています。

2.ブール分布を QRS 持続時間のデータに近似させ、パラメーターの推定を取得します。

PD = fitdist(X(:,5),'burr');

PD では Param プロパティにブール分布パラメーターの最尤推定があります。推定値は α = 80.4515、$$c$$ = 18.9251、$$k$$ = 0.4492 です。

3.QRS 持続時間データの cdf をプロットします。

QRScdf=cdf('burr',sortrows(X(:,5)),80.4515,18.9251,0.4492);
plot(sortrows(X(:,5)),QRScdf) 
title('QRS duration data')
xlabel('QRS Duration')

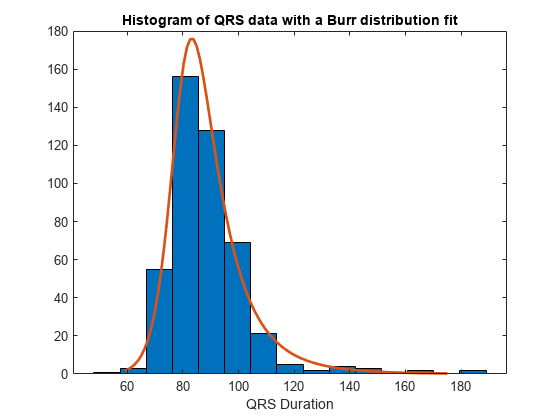
4.ビン数を 15 に指定し、ブール分布近似の pdf を使用して QRS 持続時間のヒストグラムを作成します。

histfit(X(:,5),15,'burr')
title('Histogram of QRS data with a Burr distribution fit')
xlabel('QRS Duration')

対数正規分布とブール分布の pdf の比較

対数正規分布から生成された収入データを使用して、対数正規分布の pdf をブール分布の pdf と比較します。

収入データを生成します。

rng('default') % For reproducibility
y = random('Lognormal',log(25000),0.65,[500,1]);

ブール分布を近似します。

pd = fitdist(y,'burr')

pd = 
  BurrDistribution

  Burr distribution
    alpha = 26007.2   [21165.5, 31956.4]
        c = 2.63743   [2.3053, 3.0174]
        k = 1.09658   [0.775479, 1.55064]

収入データのブール分布と対数正規分布の両方の pdf を同じ Figure にプロットします。

p_burr = pdf(pd,sortrows(y));
p_lognormal = pdf('Lognormal',sortrows(y),log(25000),0.65);
plot(sortrows(y),p_burr,'-',sortrows(y),p_lognormal,'-.')
title('Burr and Lognormal pdfs Fit to Income Data')
legend('Burr Distribution','Lognormal Distribution')

さまざまなパラメーターに対するブール分布の pdf

この例では、ブール分布の確率密度関数についてさまざまな形状を作成する方法を示します。

X = 0:0.01:5;
c = [0.5 0.95 2 5];
k = [0.5 0.75 2 5];
alpha = [0.5 1 2 5];
colors = ['b';'g';'r';'k']';

figure
for i = 1:1:4
pdf1(i,:) = pdf('burr',X,1,c(i),0.5);
pdf2(i,:) = pdf('burr',X,1,2,k(i));
pdf3(i,:) = pdf('burr',X,alpha(i),2,0.5); 

axC = subplot(3,1,1);
pC(i) = plot(X,pdf1(i,:),colors(i),'LineWidth',2);
title('Effect of c, \alpha = 1, k = 0.5'),xlabel('x') 
hold on
 
axK = subplot(3,1,2);
pK(i) = plot(X,pdf2(i,:),colors(i),'LineWidth',2);
title('Effect of k, \alpha = 1, c = 2'),xlabel('x') 
hold on 

axAlpha = subplot(3,1,3);
pAlpha(i) = plot(X,pdf3(i,:),colors(i),'LineWidth',2);
title('Effect of \alpha, c = 2, k = 0.5'),xlabel('x') 
hold on
end

set(axC,'XLim',[0 3],'YLim',[0 1.2]);
set(axK,'XLim',[0 3],'YLim',[0 2.1]);
set(axAlpha,'XLim',[0 5],'YLim',[0 1]);

legend(axC,'c=0.5','c=0.95','c=2','c=5');
legend(axK,'k=0.5','k=0.75','k=2','k=5');
legend(axAlpha,'\alpha=0.5','\alpha=1','\alpha=2','\alpha=5');

この図は、分布のパラメーターの値によって、ブール分布の形状とスケールが変化する様子を示しています。

ブール分布の生存時間関数とハザード関数

この例では、ブール分布から派生した標本の生存時間関数とハザード関数を求め、これをプロットする方法を示します。

データを生成します。

 X = 0:0.015:2.5;

X にあるデータの pdf および cdf を評価します。

Xpdf = pdf('burr',X,0.2,5,0.5);
Xcdf = cdf('burr',X,0.2,5,0.5);

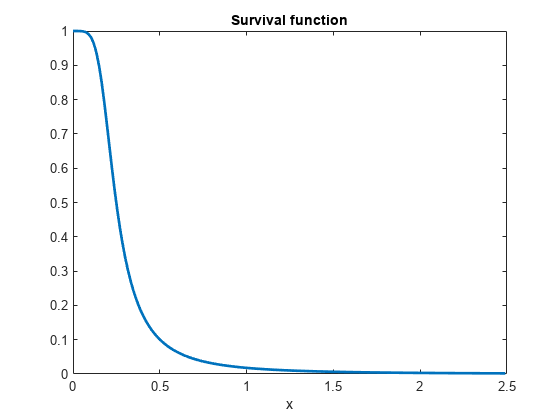
X にあるデータの生存時間関数を評価してプロットします。

S = 1.-Xcdf; % survival function
plot(X,S,'LineWidth',2)
title('Survival function')
xlabel('x')

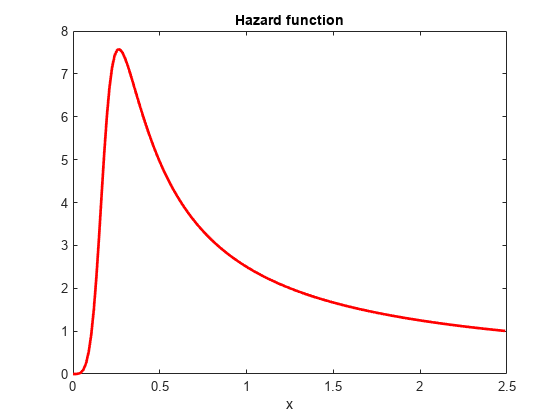
X にあるデータのハザード関数を評価してプロットします。

H = Xpdf./S; % hazard function
plot(X,H,'r','LineWidth',2)
title('Hazard function')
xlabel('x')

パラメーター推定量のダイバージェンス

この例は、ブール分布を入力データに近似させるときにパラメーター推定量が発散した場合に、表示情報を解釈する方法を示します。

1.0.5 と 2 のパラメーターを使用してワイブル分布から標本データを生成します。

rng('default') % for reproducibility
X = wblrnd(0.5,2,100,1);

2.ブール分布を近似します。

PD = fitdist(X,'burr');

Error using addburr>burrfit (line 566)
The data are not fit by a Burr distribution with finite parameters. 
The maximum likelihood fit is provided by the k->Inf, alpha->Inf 
limiting form of the Burr distribution: a Weibull distribution 
with the parameters below.
	a (scale): 0.476817
	b (shape): 1.96219

Error in prob.BurrDistribution.fit (line 246)
            p = burrfit(x,0.05,cens,freq,opt);

Error in fitdist>localfit (line 238)
pd = feval(fitter,x,'cens',c,'freq',f,varargin{:});

Error in fitdist (line 185)
    pd = localfit(dist,fitter,x,cens,freq,args{:});

このデータの近似にはワイブル群の方が適しているというエラー メッセージが表示され、ワイブル分布の近似からのパラメーター推定量が表示されます。これらの推定量を直接使用できます。近似に関してパラメーターの共分散推定やその他の情報が必要な場合、データにワイブル分布を再近似させることができます。

3.ワイブル分布をデータに近似させ、パラメーター推定量の信頼区間を求めます。

PD = fitdist(X,'weibull');
paramci(PD)

ans =

    0.4291    1.6821
    0.5298    2.2890

これらはワイブル分布近似のパラメーター推定量の 95% の信頼区間です。

参照

[1] Burr, Irving W. “Cumulative frequency functions.” The Annals of Mathematical Statistics, Vol. 13, Number 2, 1942, pp. 215–232.

[2] Tadikamalla, Pandu R. “A look at the Burr and related distributions.” International Statistical Review, Vol. 48, Number 3, 1980, pp. 337–344.

[3] Rodriguez, Robert N. “A guide to the Burr type XII distributions.” Biometrika, Vol. 64, Number 1, 1977, pp. 129–134.

[4] Al-Hussaini, Essam K. “A characterization of the Burr type XII distribution”. Appl. Math. Lett. Vol. 4, Number 1, 1991, pp. 59–61.

[5] Grammig, Joachim and Kai-Oliver Maurer. “Non-monotonic hazard functions and the autoregressive conditional duration model.” Econometrics Journal, Vol. 3, 2000, pp. 16–38.

参考

BurrDistribution

関連するトピック

• 確率分布の操作
• サポートされている分布