ガンマ分布

概要

ガンマ分布は、2 パラメーターの曲線群です。ガンマ分布は、指数分布に従う確率変数の和をモデル化し、カイ二乗分布と指数分布を一般化します。

Statistics and Machine Learning Toolbox™ には、ガンマ分布を処理する方法がいくつか用意されています。

• 確率分布を標本データに当てはめる (fitdist) かパラメーター値を指定する (makedist) ことにより、確率分布オブジェクト GammaDistribution を作成します。そして、オブジェクト関数を使用して、分布の評価や乱数の生成などを行います。

• 分布フィッター アプリを使用して、ガンマ分布を対話的に処理します。オブジェクトをアプリからエクスポートしてオブジェクト関数を使用できます。

• 分布パラメーターを指定して、分布特有の関数 (gamcdf、gampdf、gaminv、gamlike、gamstat、gamfit、gamrnd、randg) を使用します。分布特有の関数では、複数のガンマ分布についてのパラメーターを受け入れることができます。

• 分布名 ('Gamma') とパラメーターを指定して、汎用の分布関数 (cdf、icdf、pdf、random) を使用します。

パラメーター

ガンマ分布は、次のパラメーターを使用します。

パラメーター	説明	サポート
a	形状	a > 0
b	スケール	b > 0

標準ガンマ分布は単位スケールです。

形状パラメーターが a₁ および a₂ で、スケール パラメーターがいずれも b である 2 つのガンマ確率変数の和は、形状パラメーター a = a₁ + a₂、スケール パラメーター b のガンマ確率変数になります。

パラメーター推定

"尤度関数" は、パラメーターの関数として見た場合の確率密度関数 (pdf) です。"最尤推定量" (MLE) は、x の値を固定した状態で尤度関数が最大になるパラメーター推定値です。

ガンマ分布の a および b の最尤推定量は、次の連立方程式の解です。

$$\begin{array}{c}\log \widehat{a}-\psi (\widehat{a})=\log \left(\overline{x}/{\left({\displaystyle \prod _{i=1}^n{x}_i}\right)}^{1/n}\right)\\ \widehat{b}=\frac{\overline{x}}{\widehat{a}}\end{array}$$

ここで、$$\overline{x}$$ は標本 x₁, x₂, …, x_n, の標本平均で、Ψ はディガンマ関数 psi です。

ガンマ分布をデータに当てはめてパラメーター推定値を求めるには、gamfit、fitdist または mle を使用します。パラメーター推定を返す gamfit および mle と異なり、fitdist は当てはめた確率分布オブジェクト GammaDistribution を返します。オブジェクト プロパティ a および b にはパラメーター推定が格納されます。

たとえば、データへのガンマ分布の当てはめを参照してください。

確率密度関数

ガンマ分布の確率密度関数は次のようになります。

$$y=f(x|a,b)=\frac{1}{b^a\Gamma (a)}{x}^{a-1}{e}^{\frac{-x}{b}},$$

ここで、Γ( · ) はガンマ関数です。

たとえば、ガンマ分布の確率密度関数の計算を参照してください。

累積分布関数

ガンマ分布の累積分布関数 (cdf) は次のようになります。

$$p=F(x|a,b)=\frac{1}{b^a\Gamma (a)}{\displaystyle \underset{0}{\overset{x}{\int }}{t}^{a-1}{e}^{\frac{-t}{b}}dt}.$$

結果 p は、パラメーター a および b をもつガンマ分布に従う単一の観測値が区間 [0 x] に含まれる確率です。

たとえば、ガンマ分布の累積分布関数の計算を参照してください。

ガンマ cdf は、次によって、不完全ガンマ関数 gammainc と関連付けられます。

$$f\left(x|a,b\right)=\text{gammainc}\left(\frac{x}{b},a\right).$$

逆累積分布関数

ガンマ分布の逆累積分布関数 (icdf) をガンマ累積分布関数で表すと、次のようになります。

$$x=F^{-1}(p|a,b)=\{x:F(x|a,b)=p\},$$

ここで

$$p=F(x|a,b)=\frac{1}{b^a\Gamma (a)}{\displaystyle \underset{0}{\overset{x}{\int }}{t}^{a-1}{e}^{\frac{-t}{b}}dt}.$$

結果 x は、パラメーター a および b をもつガンマ分布に従う観測値が p の確率で範囲 [0 x] に含まれるような値です。

上記の積分方程式には、既知の解析的な解は存在しません。gaminv は、解の収束に反復アプローチ (ニュートン法) を使用します。

記述統計

ガンマ分布の平均は ab です。

一様分布の分散は ab² です。

例

データへのガンマ分布の当てはめ

形状 3、スケール 5 の 100 個のガンマ乱数の標本を生成します。

x = gamrnd(3,5,100,1);

fitdist を使用してガンマ分布をデータに当てはめます。

pd = fitdist(x,'gamma')

pd = 
  GammaDistribution

  Gamma distribution
    a =  2.7783   [2.1374, 3.61137]
    b = 5.73438   [4.30198, 7.64372]

fitdist は、GammaDistribution オブジェクトを返します。パラメーター推定の横にある区間は分布パラメーターの 95% 信頼区間です。

分布関数を使用して、パラメーター a と b を推定します。

[muhat,muci] = gamfit(x) % Distribution specific function

muhat = 1×2

    2.7783    5.7344

muci = 2×2

    2.1374    4.3020
    3.6114    7.6437

[muhat2,muci2] = mle(x,'distribution','gamma') % Generic function

muhat2 = 1×2

    2.7783    5.7344

muci2 = 2×2

    2.1374    4.3020
    3.6114    7.6437

ガンマ分布の確率密度関数の計算

いくつかの形状パラメーターとスケール パラメーターを使用して、ガンマ分布の pdf を計算します。

x = 0:0.1:50;
y1 = gampdf(x,1,10);
y2 = gampdf(x,3,5);
y3 = gampdf(x,6,4);

pdf をプロットします。

figure;
plot(x,y1)
hold on
plot(x,y2)
plot(x,y3)
hold off
xlabel('Observation')
ylabel('Probability Density')
legend('a = 1, b = 10','a = 3, b = 5','a = 6, b = 4')

ガンマ分布の累積分布関数の計算

いくつかの形状パラメーターとスケール パラメーターを使用して、ガンマ分布の cdf を計算します。

x = 0:0.1:50;
y1 = gamcdf(x,1,10);
y2 = gamcdf(x,3,5);
y3 = gamcdf(x,6,4);

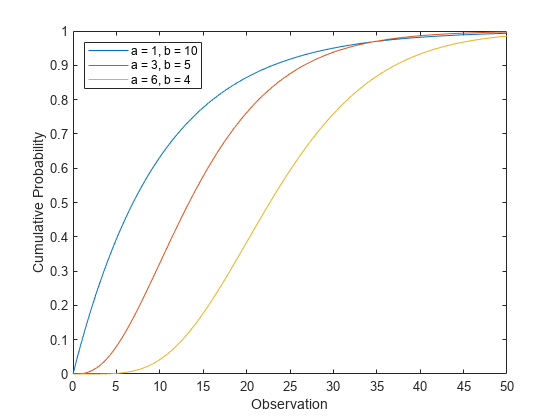
cdf をプロットします。

figure;
plot(x,y1)
hold on
plot(x,y2)
plot(x,y3)
hold off
xlabel('Observation')
ylabel('Cumulative Probability')
legend('a = 1, b = 10','a = 3, b = 5','a = 6, b = 4',"Location","northwest")

ガンマ分布と正規分布の pdf の比較

ガンマ分布には、形状パラメーター $\mathit{a}$ とスケール パラメーター $\mathit{b}$ があります。$\mathit{a}$ が大きくなると、ガンマ分布は平均 $\mu =\mathit{ab}$ および分散 ${\sigma }^2=\mathit{a}{\mathit{b}}^2$ をもつ正規分布に近づきます。

a = 100 および b = 5 の各パラメーターを使用してガンマ分布の確率密度関数を計算します。

a = 100;
b = 5;
x = 250:750;
y_gam = gampdf(x,a,b);

比較のために、ガンマによって近似される正規分布の平均、標準偏差、pdf を計算します。

mu = a*b

mu = 
500

sigma = sqrt(a*b^2)

sigma = 
50

y_norm = normpdf(x,mu,sigma);

ガンマ分布と正規分布の確率密度関数を、同じ Figure にプロットします。

plot(x,y_gam,'-',x,y_norm,'-.')
title('Gamma and Normal pdfs')
xlabel('Observation')
ylabel('Probability Density')
legend('Gamma Distribution','Normal Distribution')

正規分布の pdf はガンマ分布の pdf に近づきます。

関連する分布

• ベータ分布 — ベータ分布分布は、2 パラメーターの連続分布です。a (1 番目の形状パラメーター) および b (2 番目の形状パラメーター) のパラメーターをもちます。X₁ および X₂ が、それぞれ形状パラメーター a₁ および a₂ をもつ標準ガンマ分布に従う場合、$$Y=\frac{X_1}{X_1\text{}+X_2}$$ は、形状パラメーターが a₁ および a₂ であるベータ分布に従います。

• カイ二乗分布 — カイ二乗分布は、1 パラメーターの連続分布です。ν (自由度) のパラメーターをもちます。カイ二乗分布は、2a = ν かつ b = 2 のガンマ分布と等しくなります。

• 指数分布 — 指数分布は、1 パラメーターの連続分布です。μ (平均) のパラメーターをもちます。指数分布は、a = 1 かつ b = μ であるガンマ分布と等しくなります。平均 μ をもつ指数分布に従う k 個の確率変数の和は、a = k および μ = b のパラメーターをもつガンマ分布になります。

• 仲上分布 — 仲上分布は、2 パラメーターの連続分布です。形状パラメーター µ およびスケール パラメーター ω をもちます。x が仲上分布である場合、x² は a = μ および ab = ω であるガンマ分布になります。

• 正規分布 — 正規分布は、2 パラメーターの連続分布です。μ (平均) および σ (標準偏差) のパラメーターをもちます。a が大きいとき、ガンマ分布は μ = ab かつ σ² = ab² の正規分布に近づきます。たとえば、ガンマ分布と正規分布の pdf の比較を参照してください。

参照

[1] Abramowitz, Milton, and Irene A. Stegun, eds. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. 9. Dover print.; [Nachdr. der Ausg. von 1972]. Dover Books on Mathematics. New York, NY: Dover Publ, 2013.

[2] Evans, Merran, Nicholas Hastings, and Brian Peacock. Statistical Distributions. 2nd ed. New York: J. Wiley, 1993.

[3] Hahn, Gerald J., and Samuel S. Shapiro. Statistical Models in Engineering. Wiley Classics Library. New York: Wiley, 1994.

[4] Lawless, Jerald F. Statistical Models and Methods for Lifetime Data. 2nd ed. Wiley Series in Probability and Statistics. Hoboken, N.J: Wiley-Interscience, 2003.

[5] Meeker, William Q., and Luis A. Escobar. Statistical Methods for Reliability Data. Wiley Series in Probability and Statistics. Applied Probability and Statistics Section. New York: Wiley, 1998.

[6] Marsaglia, George, and Wai Wan Tsang. “A Simple Method for Generating Gamma Variables.” ACM Transactions on Mathematical Software 26, no. 3 (September 1, 2000): 363–72. https://doi.org/10.1007/978-1-4613-8643-8.

参考

GammaDistribution | gamcdf | gampdf | gaminv | gamlike | gamstat | gamfit | gamrnd | randg | makedist | fitdist

関連するトピック

• 確率分布の操作
• サポートされている分布