ベータ分布

概要

ベータ分布は、区間 [0,1] でのみ非ゼロになる曲線群として表されます。関数のより一般的なものは、区間の両端にパラメーターを割り当てるものです。

Statistics and Machine Learning Toolbox™ には、ベータ分布を操作する方法がいくつか用意されています。次のアプローチを使用して、標本データからのパラメーターの推定、pdf、cdf および icdf の計算、乱数の生成などを行うことができます。

確率分布オブジェクトで標本データを近似するか、パラメーター値を指定して確率分布オブジェクトを作成する。詳細は、Using BetaDistribution Objects を参照してください。
確率密度関数を使用して、行列、テーブルおよびデータセット配列から入力したデータを操作する。ベータ分布関数の一覧については、サポートされている分布を参照してください。
アプリまたはユーザーインターフェイスを使用して対話的に分布から乱数を生成、近似、調査および生成する。

これらの各オプションについての詳細は、確率分布の操作を参照してください。

パラメーター

ベータ分布は、次のパラメーターを使用します。

パラメーター	説明	サポート
`a`	最初の形状パラメーター	$a > 0$
`b`	2 番目の形状パラメーター	$b > 0$

確率密度関数

ベータ関数の確率密度関数 (pdf) は次のようになります。

$y = f (x | a, b) = \frac{1}{B (a, b)} x^{a - 1} {(1 - x)}^{b - 1} I_{[0, 1]} (x)$

ここで、B( · ) はベータ関数です。インジケーター関数 I_[0,1](x) は、"x" の値が [0,1] の範囲にある場合のみ非ゼロの確率になることを保証します。

例については、ベータ分布の pdf のプロットを参照してください。

累積分布関数

x が与えられ、a および b のペアが与えられている場合、ベータ累積分布関数は次の式で表されます。

$p = F (x | a, b) = \frac{1}{B (a, b)} \int_{0}^{x} t^{a - 1} {(1 - t)}^{b - 1} d t$

ここで、B( · ) はベータ関数です。ベータ累積分布関数は、不完全ベータ関数と同じです。

例

ベータ分布の pdf のプロット

ライブスクリプトを開く

ベータ分布のパラメーターの値を変更して、確率分布関数 (pdf) の形状に変化を加えます。

3 つのベータ分布の pdf を計算します。1 つは形状パラメーター "a" および "b" が 0.75 で、1 つはパラメーターが 1 で、もう 1 つはパラメーターが 4 です。

x = 0:0.01:1;
y1 = betapdf(x,0.75,0.75);
y2 = betapdf(x,1,1);
y3 = betapdf(x,4,4);

3 つの pdf をプロットします。

plot(x,y1)
hold on
plot(x,y2)
plot(x,y3)
legend(["a = b = 0.75","a = b = 1","a = b = 4"]);
hold off

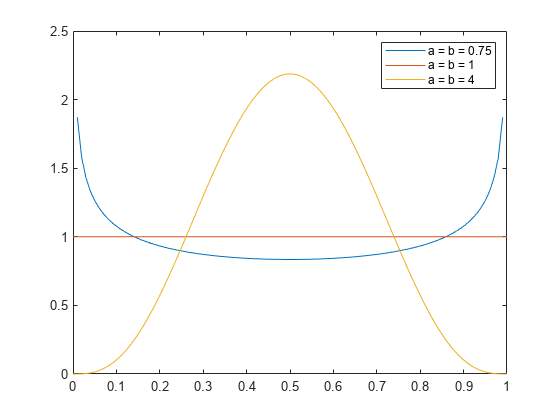
Figure contains an axes object. The axes object contains 3 objects of type line. These objects represent a = b = 0.75, a = b = 1, a = b = 4.

一定値の pdf (平らな線) をもつ標準一様分布は、ベータ分布の特殊なケースを示しています。これは、パラメーター "a" および "b" が 1 と等しい場合に発生します。

ベータ分布のパラメーターの推定

ライブスクリプトを開く

ベータ分布のパラメーターの最尤推定量 (MLE) を計算します。

尤度関数を最大にする方法は、パラメーターの推定でよく使用される手法です。尤度関数は、ベータ確率分布関数 (pdf) と同じ形式をしています。ただし、pdf において、パラメーターは既知の定数であり、変数は x です。尤度関数は、この関係が逆になります。つまり、標本値 (x の値) が既に観測されていて固定の定数であり、変数が未知のパラメーターです。最尤推定法では、あるデータ集合において、尤度が最も高くなるパラメーターの値を計算します。

"a" が 5、"b" が 0.2 に等しいベータ分布から 100 個の乱数を生成します。関数 betafit は、ベータ分布のパラメーターについて、最尤推定と信頼区間を出力します。

rng("default") % For reproducibility
r = betarnd(5,0.2,100,1);
[phat, pci] = betafit(r)

phat = 1×2

    7.4911    0.2135

pci = 2×2

    5.0861    0.1744
   11.0334    0.2614

パラメーター "a" の MLE は 7.4911 です。"a" の 95% 信頼区間の範囲は 5.0861 から 11.0334 で、真の値 5 が含まれていません。この結果になる確率は高くありませんが、分布パラメーターの推定時に発生することがあります。

パラメーター "b" の MLE は 0.2135 です。"b" の 95% 信頼区間の範囲は 0.1744 から 0.2614 で、真の値 0.2 が含まれています。

参考

BetaDistribution