カイ二乗分布

概要

カイ二乗 (χ²) 分布は、1 パラメーターの曲線群です。カイ二乗分布は仮説検定で一般的に使用され、特に、適合度についてはカイ二乗検定が利用されます。

Statistics and Machine Learning Toolbox™ には、カイ二乗分布を処理する方法がいくつか用意されています。

• 分布パラメーターを指定して、分布特有の関数 (chi2cdf、chi2inv、chi2pdf、chi2rnd、chi2stat) を使用します。分布特有の関数では、複数のカイ二乗分布についてのパラメーターを受け入れることができます。

• 分布名 ('Chisquare') とパラメーターを指定して、汎用の分布関数 (cdf、icdf、pdf、random) を使用します。

パラメーター

カイ二乗分布は、次のパラメーターを使用します。

パラメーター	説明	サポート
nu (ν)	自由度	ν = 1, 2, 3,...

通常、自由度のパラメーターは整数ですが、カイ二乗関数は任意の正の値を受け付けます。

自由度 ν₁ および ν₂ の 2 つのカイ二乗確率変数の和は、自由度 ν = ν₁ + ν₂ のカイ二乗確率変数です。

確率密度関数

カイ二乗分布の確率密度関数 (pdf) は次のようになります。

$$y=f\left(x|\nu \right)=\frac{x^{\left(\nu -2\right)/2}{e}^{-x/2}}{2^{\frac{\nu }{2}}\Gamma \left(\nu /2\right)},$$

ここで、ν は自由度、Γ( · ) はガンマ関数です。

たとえば、カイ二乗分布の確率密度関数の計算を参照してください。

累積分布関数

カイ二乗分布の累積分布関数 (cdf) は次のようになります。

$$p=F(x|\nu )={\displaystyle {\int }_0^x\frac{t^{(\nu -2)/2}{e}^{-t/2}}{2^{\nu /2}\Gamma (\nu /2)}dt},$$

ここで、ν は自由度、Γ( · ) はガンマ関数です。結果 p は、自由度 ν のカイ二乗分布に従う単一の観測値が区間 [0, x] に含まれる確率です。

たとえば、カイ二乗分布の累積分布関数の計算を参照してください。

逆累積分布関数

カイ二乗分布の逆累積分布関数 (icdf) は次のようになります。

$$x=F^{-1}(p|\nu )=\{x:F(x|\nu )=p\},$$

ここで

$$p=F(x|\nu )={\displaystyle {\int }_0^x\frac{t^{(\nu -2)/2}{e}^{-t/2}}{2^{\nu /2}\Gamma (\nu /2)}}dt,$$

ν は自由度、Γ( · ) はガンマ関数です。結果 p は、自由度 ν のカイ二乗分布に従う単一の観測値が区間 [0, x] に含まれる確率です。

記述統計

カイ二乗分布の平均は ν です。

カイ二乗分布の分散は 2ν です。

例

カイ二乗分布の確率密度関数の計算

自由度が 4 のカイ二乗分布の確率密度関数を計算します。

x = 0:0.2:15;
y = chi2pdf(x,4);

確率密度関数をプロットします。

figure;
plot(x,y)
xlabel('Observation')
ylabel('Probability Density')

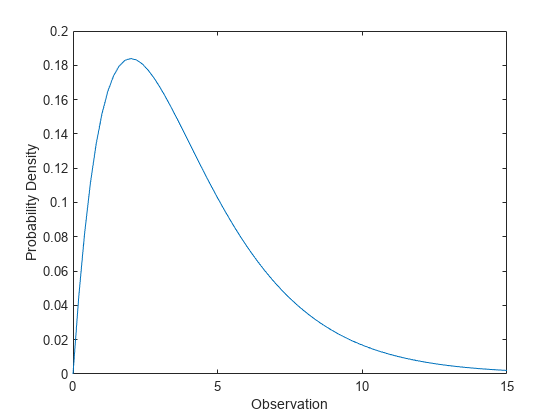
カイ二乗分布は右側に歪みます。特に自由度が小さい場合にこの傾向が強くなります。

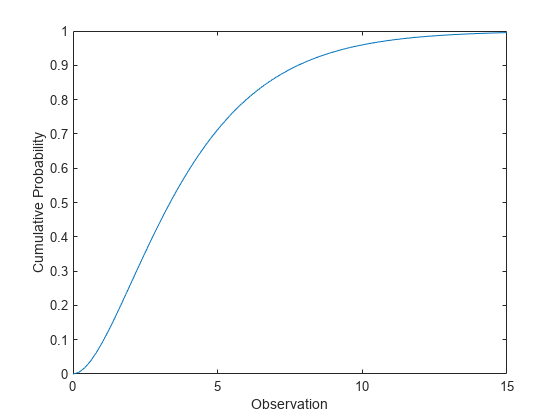
カイ二乗分布の累積分布関数の計算

自由度が 4 のカイ二乗分布の cdf を計算します。

x = 0:0.2:15;
y = chi2cdf(x,4);

累積分布関数をプロットします。

figure;
plot(x,y)
xlabel('Observation')
ylabel('Cumulative Probability')

関連する分布

• F 分布 — F 分布は、2 パラメーターの分布です。ν₁ (分子の自由度) および ν₂ (分母の自由度) のパラメーターをもちます。F 分布は、比 $$F=\frac{\raisebox{1ex}{${\chi }_1^2$}\!\left/ \!\raisebox{-1ex}{${\nu }_1$}\right.}{\raisebox{1ex}{${\chi }_2^2$}\!\left/ \!\raisebox{-1ex}{${\nu }_2$}\right.}$$ として定義できます。ここで、χ²₁ と χ²₂ は、それぞれ ν₁ と ν₂ の自由度をもつカイ二乗分布です。

• ガンマ分布 — ガンマ分布は、2 パラメーターの連続分布です。a (形状) および b (スケール) のパラメーターをもちます。カイ二乗分布は、2a = ν かつ b = 2 のガンマ分布と等しくなります。

• 非心カイ二乗分布 — 非心カイ二乗分布は、2 パラメーターの連続分布です。ν (自由度) および δ (非心度) のパラメーターをもちます。δ = 0 のとき、非心カイ二乗分布はカイ二乗分布と等しくなります。

• 正規分布 — 正規分布は、2 パラメーターの連続分布です。μ (平均) および σ (標準偏差) のパラメーターをもちます。標準正規分布は、μ = 0 かつ σ = 1 のときに発生します。

  Z₁, Z₂, …, Z_n が標準正規確率変数である場合、$${\displaystyle \sum _{i=1}^n{Z}_i{}^2}$$ は自由度 ν = n – 1 のカイ二乗分布に従います。

  n 個の観測値の集合が分散 σ² と標本分散 s² の正規分布に従う場合、$$\frac{\left(n-1\right)s^2}{{\sigma }^2}$$ は自由度 ν = n – 1 のカイ二乗分布に従います。この関係は、関数 normfit 内で推定の正規パラメーター σ² の信頼区間を計算するために使用されます。

• スチューデントの t 分布 — スチューデントの t 分布は、1 パラメーターの連続分布です。ν (自由度) のパラメーターをもちます。Z が正規分布で、χ² が自由度 ν のカイ二乗分布に従う場合、$$\text{t = }\frac{Z}{\sqrt{{\chi }^2/\nu }}$$ は自由度 ν のスチューデントの t 分布に従います。

• ウィシャート分布 — ウィシャート分布は、カイ二乗分布の多次元版です。

参照

[1] Abramowitz, Milton, and Irene A. Stegun, eds. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. 9. Dover print.; [Nachdr. der Ausg. von 1972]. Dover Books on Mathematics. New York, NY: Dover Publ, 2013.

[2] Devroye, Luc. Non-Uniform Random Variate Generation. New York, NY: Springer New York, 1986. https://doi.org/10.1007/978-1-4613-8643-8

[3] Evans, M., N. Hastings, and B. Peacock. Statistical Distributions. 2nd ed., Hoboken, NJ: John Wiley & Sons, Inc., 1993.

[4] Kreyszig, Erwin. Introductory Mathematical Statistics: Principles and Methods. New York: Wiley, 1970.

参考

chi2cdf | chi2pdf | chi2inv | chi2stat | chi2gof | chi2rnd

関連するトピック

• 確率分布の操作
• サポートされている分布

×

例を開く

この例の変更されたバージョンがあります。編集された方の例を開きますか?

いいえ、変更されたバージョンを上書きします。 はい