スチューデントの t 分布
概要
スチューデントの t 分布は、1 パラメーターの曲線群です。この分布は、通常、母標準偏差が未知の場合の母集団平均に関する仮説を検定するのに使用されます。
Statistics and Machine Learning Toolbox™ には、スチューデント t 分布を処理する方法がいくつか用意されています。
パラメーター
スチューデント t 分布は、次のパラメーターを使用します。
| パラメーター | 説明 | サポート |
|---|---|---|
| nu (ν) | 自由度 | ν = 1, 2, 3,... |
確率密度関数
スチューデントの t 分布の pdf は次のようになります。
ここで、ν は自由度、Γ( · ) はガンマ関数です。結果 y は、自由度が ν のスチューデント t 分布から x の特定の値を観測する確率です。
たとえば、スチューデントの t 分布の確率密度関数の計算とプロットを参照してください。
累積分布関数
スチューデント t 分布の cdf は次のようになります。
ここで、ν は自由度、Γ( · ) はガンマ関数です。結果 p は、自由度が ν である t 分布に従う単一の観測値が区間 [–∞, x] に含まれる確率です。
たとえば、スチューデントの t 分布の累積分布関数の計算とプロットを参照してください。
逆累積分布関数
逆関数 t は、スチューデント t 累積分布関数を使用して、次のように定義されます。
ここで
ν は自由度、Γ( · ) はガンマ関数です。結果 x は、確率 p を指定した積分方程式の解です。
たとえば、スチューデントの t 累積分布逆関数の計算を参照してください。
記述統計
自由度 ν が 1 より大きい場合、スチューデント t 分布の平均は μ = 0 となります。ν が 1 に等しい場合、平均は定義されません。
自由度 ν が 2 より大きい場合、スチューデント t 分布の分散は となります。ν が 2 以下の場合、分散は定義されません。
例
スチューデントの t 分布の確率密度関数の計算とプロット
自由度が 5、10、50 に等しいスチューデントの t 分布の pdf を計算します。
x = [-5:.1:5]; y1 = tpdf(x,5); y2 = tpdf(x,10); y3 = tpdf(x,50);
選択した 3 つの nu についての pdf を同じ軸にプロットします。
figure; plot(x,y1,'Color','black','LineStyle','-') hold on plot(x,y2,'Color','red','LineStyle','-.') plot(x,y3,'Color','blue','LineStyle','--') xlabel('Observation') ylabel('Probability Density') legend({'nu = 5','nu = 10','nu = 50'}) hold off

スチューデントの t 分布の累積分布関数の計算とプロット
自由度が 5、10、50 に等しいスチューデントの t 分布の cdf を計算します。
x = [-5:.1:5]; y1 = tcdf(x,5); y2 = tcdf(x,10); y3 = tcdf(x,50);
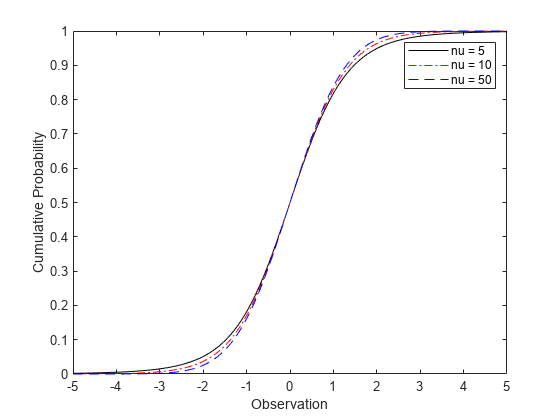
選択した 3 つの nu についての cdf を同じ軸にプロットします。
figure; plot(x,y1,'Color','black','LineStyle','-') hold on plot(x,y2,'Color','red','LineStyle','-.') plot(x,y3,'Color','blue','LineStyle','--') xlabel('Observation') ylabel('Cumulative Probability') legend({'nu = 5','nu = 10','nu = 50'}) hold off
スチューデントの t 累積分布逆関数の計算
自由度 50 のスチューデントの t 分布から、95 番目の百分位数を求めます。
p = .95; nu = 50; x = tinv(p,nu)
x = 1.6759
スチューデントの t 分布と正規分布の pdf の比較
スチューデントの t 分布は、単一のパラメーター ν (自由度) に依存する曲線族です。自由度 ν が無限大に近づくと、t 分布は標準正規分布に近づきます。
パラメーター nu = 5 をもつスチューデントの t 分布とパラメーター nu = 15 をもつスチューデントの t 分布の pdf を計算します。
x = [-5:0.1:5]; y1 = tpdf(x,5); y2 = tpdf(x,15);
標準正規分布の pdf を計算します。
z = normpdf(x,0,1);
スチューデントの t 分布の pdf と標準正規分布の pdf を、同じ Figure にプロットします。
plot(x,y1,'-.',x,y2,'--',x,z,'-') legend('Student''s t Distribution with \nu=5', ... 'Student''s t Distribution with \nu=15', ... 'Standard Normal Distribution','Location','best') xlabel('Observation') ylabel('Probability Density') title('Student''s t and Standard Normal pdfs')

標準正規分布の pdf は、スチューデントの t 分布の pdf より裾が短くなっています。
関連する分布
ベータ分布 — ベータ分布分布は、2 パラメーターの連続分布です。a (1 番目の形状パラメーター) および b (2 番目の形状パラメーター) のパラメーターをもちます。Y が、自由度 ν のスチューデントの t 分布に従う場合、 は、形状パラメーターが a = ν/2 および b = ν/2 であるベータ分布になります。t 分布の累積分布関数と逆関数の値を計算する場合や、t 分布に従う乱数を生成する場合に、この関係が使用されます。
コーシー分布 — コーシー分布は、2 パラメーターの連続分布です。γ (スケール) および δ (位置) のパラメーターをもちます。これは、形状パラメーター α = 1 および β = 0 をもつ安定分布の特殊なケースです。標準コーシー分布 (単位スケールかつ位置 0) は、1 に等しい自由度 ν をもつスチューデントの t 分布です。標準コーシー分布では、平均と分散が定義されません。
たとえば、スチューデントの t を使用したコーシー乱数の生成を参照してください。
カイ二乗分布 — カイ二乗分布は、1 パラメーターの連続分布です。ν (自由度) のパラメーターをもちます。Z が標準正規分布、χ2 がカイ二乗分布、Z および χ2 が自由度 νで独立である場合、 は自由度 ν のスチューデントの t 分布に従います。
非心 t 分布 — 非心 t 分布は、スチューデントの t 分布を一般化する 2 パラメーターの連続分布です。ν (自由度) および δ (非心度) のパラメーターをもちます。δ = 0 に設定すると、スチューデントの t 分布になります。
正規分布 — 正規分布は、2 パラメーターの連続分布です。μ (平均) および σ (標準偏差) のパラメーターをもちます。
自由度 ν が無限大に近づくと、スチューデントの t 分布は標準正規分布 (ゼロ平均かつ単位標準偏差) に近づきます。
例については、スチューデントの t 分布と正規分布の pdf の比較を参照してください。
x が平均 μ の正規分布に従うサイズ n の無作為標本である場合、 を標本平均、s を標本標準偏差とする統計量 は、自由度 n —1 をもつスチューデントの t 分布に従います。
たとえば、スチューデントの t 分布の累積分布関数の計算を参照してください。
t 位置-スケール分布 — t 位置-スケール分布は、3 パラメーターの連続分布です。μ (平均)、σ (スケール)、および ν (形状) のパラメーターをもちます。x が、パラメーター µ、σ、および ν をもつ t 位置-スケール分布である場合、 は自由度 ν のスチューデントの t 分布に従います。
参照
[1] Abramowitz, Milton, and Irene A. Stegun, eds. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. 9. Dover print.; [Nachdr. der Ausg. von 1972]. Dover Books on Mathematics. New York, NY: Dover Publ, 2013.
[2] Devroye, Luc. Non-Uniform Random Variate Generation. New York, NY: Springer New York, 1986. https://doi.org/10.1007/978-1-4613-8643-8
[3] Evans, Merran, Nicholas Hastings, and Brian Peacock. Statistical Distributions. 2nd ed. New York: J. Wiley, 1993.
[4] Kreyszig, Erwin. Introductory Mathematical Statistics: Principles and Methods. New York: Wiley, 1970.
参考
tcdf | tpdf | tinv | tstat | trnd | ttest | ttest2