安定分布

概要

安定分布は、大きい裾および歪度のモデル化に適している確率分布のクラスです。同一の安定分布に従う 2 つの独立した確率変数の線形結合は、個々の変数と同じ分布になります。つまり、X₁、X₂、...、X_n が同一の安定分布に従う独立した確率変数である場合、すべての n について次のようになります。

$$X_1+X_2+\dots +X_n\stackrel{d}{=}{c}_{n}X+d_n$$

ここで、定数は c_n > 0 および $$d_n\in ℝ$$ です。

安定分布は、同一分布に従う独立した変数の正規和の極限は安定するという一般化中心極限定理の応用です。

安定分布には、いくつかの異なるパラメーター表現があります。Statistics and Machine Learning Toolbox™ の実装では、[2] に記載されているパラメーター表現を使用しています。このケースでは、特性関数が次によって与えられる場合、確率変数 X は安定分布 $$S\left(\alpha ,\beta ,\gamma ,\delta ;0\right)$$ に従います。

$$E\left(e^{itX}\right)=\{\begin{array}{c}\exp \left(-{\gamma }^{\alpha }{\left|t\right|}^{\alpha }\left[1+i\beta \text{sign}\left(t\right)\tan \frac{\pi \alpha }{2}\left({\left(\gamma \left|t\right|\right)}^{1-\alpha }-1\right)\right]+i\delta t\right)for\alpha \ne 1,\\ \exp \left(-\gamma \left|t\right|\left[1+i\beta \text{sign}\left(t\right)\frac{2}{\pi }\ln \left(\gamma \left|t\right|\right)\right]+i\delta t\right)for\alpha =1\end{array}$$

パラメーター

安定分布では次のパラメーターを使用します。

パラメーター	説明	サポート
alpha	最初の形状パラメーター	0 < α ≤ 2
beta	2 番目の形状パラメーター	-1 ≤ β ≤ 1
gam	スケール パラメーター	0 < γ < ∞
delta	位置パラメーター	-∞ < δ < ∞

1 番目の形状パラメーター α は分布の裾を表しています。安定分布の密度は直接積分法を使用して計算されます。[1]で説明されているように、パラメーター α が 1 または 0 に近い場合は pdf と cdf を数値的に正確に計算することは困難です。α が 1 に近い場合 (具体的には $$0<\left|\alpha -1\right|<0.02$$)、α は 1 に丸められます。α が 0 に近い場合、密度が不正確になる可能性があります。

2 番目の形状パラメーター β は分布の歪度を表しています。β = 0 の場合、分布は対称的になります。β > 0 の場合、右の裾が長い分布になります。β < 0 の場合、左の裾が長い分布になります。α が小さい場合、β の歪度による影響が大きくなります。α が大きくなると、β の影響は小さくなります。

確率密度関数

定義

ほとんどの安定分布族のメンバーには明確な確率密度関数 (pdf) がありません。代わりに、pdf は特性関数に関して記述されます [2]。

正規分布、コーシー分布、レヴィ分布など、一部の特殊なケースの安定分布には、閉形式の密度関数があります。詳細については、他の分布との関係を参照してください。

安定分布の確率密度関数を計算するには、pdf を使用します。pdf の計算には直接積分法が使用されます。[1]で説明されているように、パラメーター α が 1 または 0 に近い場合は pdf を数値的に正確に計算することは困難です。α が 1 に近い場合 (具体的には $$0<\left|\alpha -1\right|<0.02$$)、α は 1 に丸められます。α が 0 に近い場合、密度が不正確になる可能性があります。

安定分布の pdf の比較

以下のプロットでは、alpha の値が異なる安定分布の確率密度関数を比較します。各ケースで beta = 0、gam = 1 および delta = 0 です。

pd1 = makedist('Stable','alpha',2,'beta',0,'gam',1,'delta',0);
pd2 = makedist('Stable','alpha',1,'beta',0,'gam',1,'delta',0);
pd3 = makedist('Stable','alpha',0.5,'beta',0,'gam',1,'delta',0);

各分布の pdf を計算します。

x = -5:.1:5;
pdf1 = pdf(pd1,x);
pdf2 = pdf(pd2,x);
pdf3 = pdf(pd3,x);

視覚的に比較するため、3 つの pdf 関数をすべて同じ図にプロットします。

figure
plot(x,pdf1,'b-');
hold on
plot(x,pdf2,'r-.');
plot(x,pdf3,'k--');
title('Compare Alpha Parameters in Stable Distribution PDF Plots')
legend('\alpha = 2','\alpha = 1','\alpha = 0.5','Location','northwest')
hold off

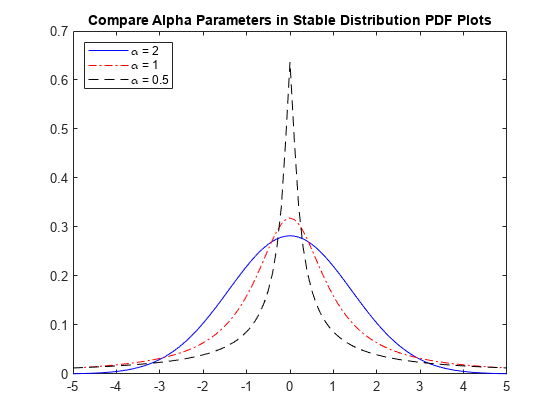
プロットには、分布の裾に対するパラメーター alpha の影響が示されています。

次のプロットでは、beta の値が異なる安定分布の確率密度関数を比較します。各ケースで alpha = 0.5、gam = 1 および delta = 0 です。

pd1 = makedist('Stable','alpha',0.5,'beta',0,'gam',1,'delta',0);
pd2 = makedist('Stable','alpha',0.5,'beta',0.5,'gam',1,'delta',0);
pd3 = makedist('Stable','alpha',0.5,'beta',1,'gam',1,'delta',0);

各分布の pdf を計算します。

x = -5:.1:5;
pdf1 = pdf(pd1,x);
pdf2 = pdf(pd2,x);
pdf3 = pdf(pd3,x);

視覚的に比較するため、3 つの pdf 関数をすべて同じ図にプロットします。

figure
plot(x,pdf1,'b-');
hold on
plot(x,pdf2,'r-.');
plot(x,pdf3,'k--');
title('Compare Beta Parameters in Stable Distribution PDF Plots')
legend('\beta = 0','\beta = 0.5','\beta = 1','Location','northwest')
hold off

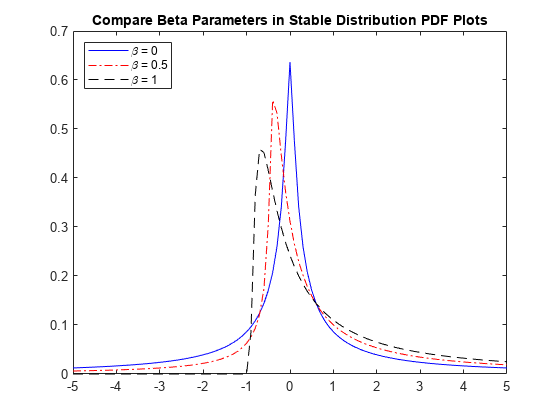
乱数発生

安定分布から乱数を生成するには、random を使用します。[3] で提案されている方法を使用して安定分布の乱数が生成されます。

累積分布関数

定義

ほとんどの安定分布族のメンバーには明確な累積分布関数 (cdf) がありません。代わりに、cdf は特性関数に関して記述されます [2]。

安定分布の累積分布関数を計算するには、cdf を使用します。cdf の計算には直接積分法が使用されます。[1]で説明されているように、パラメーター α が 1 または 0 に近い場合は cdf を数値的に正確に計算することは困難です。α が 1 に近い場合 (具体的には $$0<\left|\alpha -1\right|<0.02$$)、α は 1 に丸められます。α が 0 に近い場合、密度が不正確になる可能性があります。

安定分布の cdf の比較

以下のプロットでは、alpha の値が異なる安定分布の累積分布関数を比較します。各ケースで beta = 0、gam = 1 および delta = 0 です。

pd1 = makedist('Stable','alpha',2,'beta',0,'gam',1,'delta',0);
pd2 = makedist('Stable','alpha',1,'beta',0,'gam',1,'delta',0);
pd3 = makedist('Stable','alpha',0.5,'beta',0,'gam',1,'delta',0);

各分布の cdf を計算します。

x = -5:.1:5;
cdf1 = cdf(pd1,x);
cdf2 = cdf(pd2,x);
cdf3 = cdf(pd3,x);

視覚的に比較するため、3 つの cdf 関数をすべて同じ図にプロットします。

figure
plot(x,cdf1,'b-');
hold on
plot(x,cdf2,'r-.');
plot(x,cdf3,'k--');
title('Compare Alpha Parameters in Stable Distribution CDF Plots')
legend('\alpha = 2','\alpha = 1','\alpha = 0.5','Location','northwest')
hold off

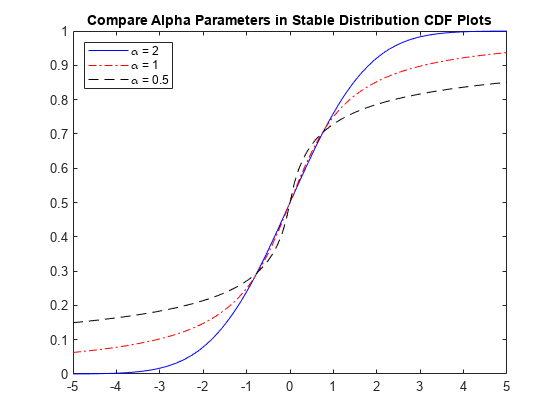
プロットには、cdf の形状に対するパラメーター alpha の影響が示されています。

次のプロットでは、beta の値が異なる安定分布の累積分布関数を比較します。すべてのケースで alpha = 0.5、gam = 1 および delta = 0 です。

pd1 = makedist('Stable','alpha',0.5,'beta',0,'gam',1,'delta',0);
pd2 = makedist('Stable','alpha',0.5,'beta',0.5,'gam',1,'delta',0);
pd3 = makedist('Stable','alpha',0.5,'beta',1,'gam',1,'delta',0);

各分布の cdf を計算します。

x = -5:.1:5;
cdf1 = cdf(pd1,x);
cdf2 = cdf(pd2,x);
cdf3 = cdf(pd3,x);

視覚的に比較するため、3 つの pdf 関数をすべて同じ図にプロットします。

figure
plot(x,cdf1,'b-');
hold on
plot(x,cdf2,'r-.');
plot(x,cdf3,'k--');
title('Compare Beta Parameters in Stable Distribution CDF Plots')
legend('\beta = 0','\beta = 0.5','\beta = 1','Location','northwest')
hold off

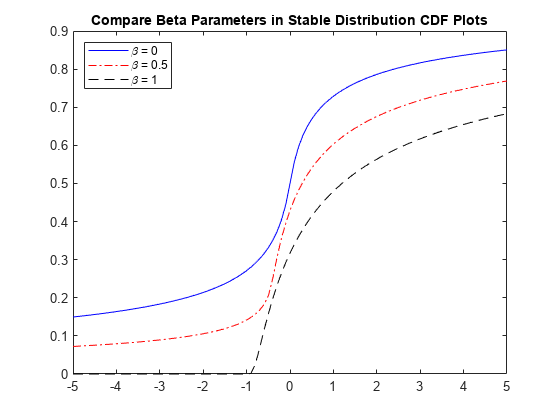
記述統計

安定分布の平均は、α ≤ 1 の値について定義されません。α > 1 の場合、安定分布の平均は次のようになります。

$$\text{mean}=\delta -\beta \gamma \tan \left(\frac{\pi \alpha }{2}\right).$$

安定分布の平均を計算するには、mean を使用します。

安定分布の分散は、α < 2 の値について定義されません。α = 2 の場合、安定分布の分散は次のようになります。

$$\mathrm{var}=2{\gamma }^2.$$

安定分布の分散を計算するには、var を使用します。

他の分布との関係

安定分布には 3 つの特殊なケースがあります。正規分布、コーシー分布およびレヴィ分布です。これらの分布は、閉形式の確率密度関数があるので重要です。

正規分布

正規分布 (ガウス分布) は、安定分布の特殊なケースです。α = 2 である安定分布は、正規分布に対応します。つまり、次のようになります。

$$N\left(\mu ,{\sigma }^2\right)=S\left(2,0,\frac{\sigma }{\sqrt{2}},\mu \right).$$

μ は正規分布の平均、σ は標準偏差です。

α = 2 の場合に β の値は影響を与えませんが、通常は正規分布は β= 0 に関連付けられます。

正規分布の確率密度関数は次のようになります。

$$f\left(x\right)=\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{{\left(x-\mu \right)}^2}{2{\sigma }^2}\right),-\infty <x<\infty .$$

正規分布の密度のプロットは、釣り鐘形の対称的な曲線になります。

コーシー分布

コーシー分布は安定分布の特殊なケースであり、α = 1 および β = 0 です。つまり、次のようになります。

$$Cauchy\left(\delta ,\gamma \right)=S\left(1,0,\gamma ,\delta \right),$$

ここで、γ はコーシー分布のスケール パラメーター、δ は位置パラメーターです。

コーシー分布の確率密度関数は次のようになります。

$$f\left(x\right)=\frac{1}{\pi }\frac{\gamma }{{\gamma }^2+{\left(x-\delta \right)}^2},-\infty <x<\infty .$$

コーシー分布の密度のプロットは、釣り鐘形の対称的な曲線になりますが、正規分布の密度より裾が広くなります。

レヴィ分布

レヴィ分布は安定分布の特殊なケースであり、α = 0.5 および β = 1 です。つまり、次のようになります。

$$Lévy\left(\delta ,\gamma \right)=S\left(0.5,1,\gamma ,\gamma +\delta \right).$$

ここで、γ はレヴィ分布のスケール パラメーター、δ は位置パラメーターです。

レヴィ分布の確率密度関数は次のようになります。

$$f\left(x\right)=\sqrt{\frac{\gamma }{2\pi }}\frac{1}{{\left(x-\delta \right)}^{3/2}}\exp \left(-\frac{\gamma }{2\left(x-\delta \right)}\right),\delta <x<\infty .$$

レヴィ分布の密度のプロットは非常に歪んでおり、裾が広くなります。

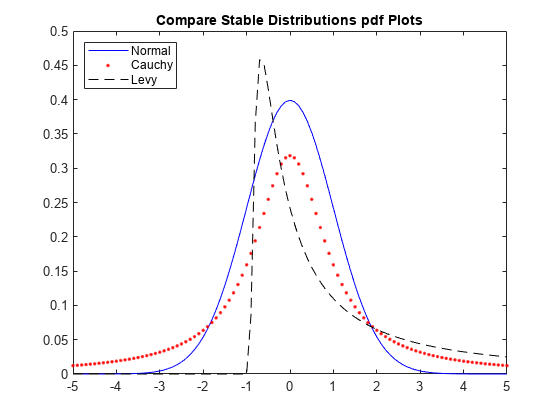
安定分布の比較プロット

以下のプロットでは、標準正規分布、コーシー分布およびレヴィ分布の確率密度関数を比較します。

標準正規分布、コーシー分布およびレヴィ分布の確率分布オブジェクトを作成します。

pd_norm = makedist('Stable','alpha',2,'beta',0,'gam',1/sqrt(2),'delta',0);
pd_cauchy = makedist('Stable','alpha',1,'beta',0,'gam',1,'delta',0);
pd_levy = makedist('Stable','alpha',0.5,'beta',1,'gam',1,'delta',0);

各分布の pdf を計算します。

x = -5:.1:5;
pdf_norm = pdf(pd_norm,x);
pdf_cauchy = pdf(pd_cauchy,x);
pdf_levy = pdf(pd_levy,x);

視覚的に比較するため、3 つの pdf 関数をすべて同じ図にプロットします。

figure
plot(x,pdf_norm,'b-');
hold on
plot(x,pdf_cauchy,'r.');
plot(x,pdf_levy,'k--');
title('Compare Stable Distributions pdf Plots')
legend('Normal','Cauchy','Levy','Location','northwest')
hold off

参照

[1] Nolan, John P. “Numerical calculation of stable densities and distribution functions.” Communications in Statistics: Stochastic Models. Vol. 13, No. 4, 1997, pp. 759–774.

[2] Nolan, John P. Univariate Stable Distributions: Models for Heavy Tailed Data. Springer International Publishing, 2020. https://doi.org/10.1007/978-3-030-52915-4.

[3] Weron, A. and R. Weron. “Computer simulation of Lévy α-stable variables and processes.” Lecture Notes in Physics. Vol. 457, 1995, pp. 379–392.

参考

StableDistribution

関連するトピック

• 確率分布の操作
• サポートされている分布