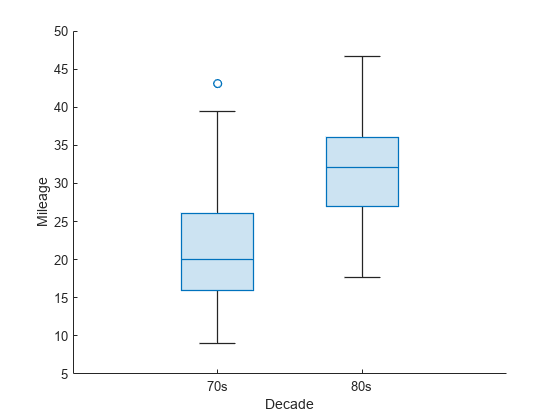
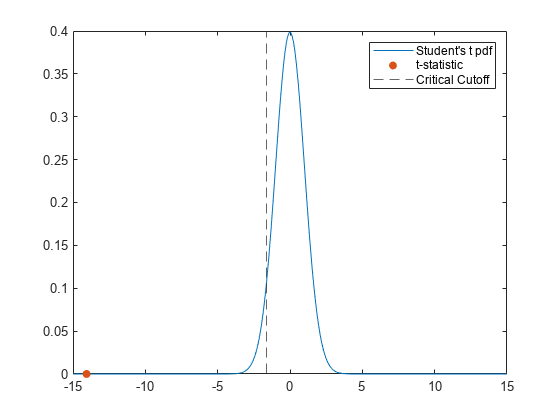
ttest2

2 標本 t 検定

ページ内をすべて折りたたむ

構文

h = ttest2(x,y)
h = ttest2(x,y,Name,Value)
[h,p] = ttest2(___)
[h,p,ci,stats] = ttest2(___)

説明

h = ttest2(x,y) は、2 標本 t 検定を使用して、ベクトル x と y のデータが、等しい平均と、等しいが未知の分散の正規分布からの独立した無作為標本から派生しているという帰無仮説の検定の判定を返します。対立仮説は、x と y のデータは、平均が等しくない母集団から派生しているとします。検定で帰無仮説が有意水準 5% で棄却された場合、結果 h は 1、それ以外の場合は 0 になります。

例

h = ttest2(x,y,Name,Value) は、1 つ以上の名前と値のペア引数で指定された追加オプションを使用して、 2 標本 t 検定の検定の判定を返します。たとえば、有意水準を変更したり、等分散を仮定せずに検定を実行することができます。

例

[h,p] = ttest2(___) は、前の構文の入力引数のいずれかを使用して、検定の p 値である p も返します。

例

[h,p,ci,stats] = ttest2(___) は、母集団平均の差に対する信頼区間 ci と、検定統計量に関する情報を含む stats 構造体も返します。

例

例

すべて折りたたむ

ライブ スクリプトを開く

データ セットを読み込みます。2 つの試験における学生の採点データを表すデータ行列の 1 列目と 2 列目を含むベクトルを作成します。 

load examgrades
x = grades(:,1);
y = grades(:,2);

2 つのデータ標本が、等しい平均の母集団から派生しているという帰無仮説を検定します。 

[h,p,ci,stats] = ttest2(x,y)
h = 
0

p = 
0.9867

ci = 2×1

   -1.9438
    1.9771


stats = struct with fields:
    tstat: 0.0167
       df: 238
       sd: 7.7084

h = 0 の戻り値は、ttest2 が既定の有意水準 5% で帰無仮説を棄却しないことを示します。

ライブ スクリプトを開く

データ セットを読み込みます。2 つの試験における学生の採点データを表すデータ行列の 1 列目と 2 列目を含むベクトルを作成します。 

load examgrades
x = grades(:,1);
y = grades(:,2);

2 つのデータ ベクトルが等しい平均の母集団から派生しているという帰無仮説を、その母集団の分散も等しいと仮定せずに検定します。 

[h,p] = ttest2(x,y,'Vartype','unequal')
h = 
0

p = 
0.9867

h = 0 の戻り値は、等しい分散が仮定されない場合であっても、ttest2 が既定の有意水準 5% で帰無仮説を棄却しないことを示します。

ライブ スクリプトを開く

標本データを読み込みます。categorical ベクトルを作成し、車両の年式に従って車両の燃費データにラベルを付けます。

load carbig.mat;

decade = categorical(Model_Year < 80,[true,false],["70s","80s"]);

年代ごとに燃費データの箱ひげ図を作成します。

boxchart(decade,MPG)
xlabel("Decade")
ylabel("Mileage")

Figure contains an axes object. The axes object with xlabel Decade, ylabel Mileage contains an object of type boxchart.

年代ごとに燃費データからベクトルを作成します。左側 2 標本 "t" 検定を使用して、等しい平均の母集団からデータが派生しているという帰無仮説を検定します。1970 年代に製造された自動車の燃費の母集団平均は 1980 年代に製造された自動車の燃費の母集団平均よりも小さいという対立仮説を使用します。

MPG70s = MPG(decade == "70s");
MPG80s = MPG(decade == "80s");

[h,~,~,stats] = ttest2(MPG70s,MPG80s,"Tail","left")
h = 
1

stats = struct with fields:
    tstat: -14.0630
       df: 396
       sd: 6.3910

h = 1 の戻り値は、ttest2 が、1970 年代に製造された自動車の燃費の母集団平均は 1980 年代に製造された自動車の燃費の母集団平均よりも小さいという対立仮説を優先して、既定の有意水準 5% で帰無仮説を棄却したことを示します。

対応するスチューデントの "t" 分布、返された "t" 統計量、および棄却限界 "t" 値をプロットします。tinv を使用して、既定の信頼水準 95% における棄却限界 "t" 値を計算します。

nu = stats.df;
k = linspace(-15,15,300);
tdistpdf = tpdf(k,nu);
tval = stats.tstat
tval = 
-14.0630

tvalpdf = tpdf(tval,nu);
tcrit = -tinv(0.95,nu)
tcrit = 
-1.6487

plot(k,tdistpdf)
hold on
scatter(tval,tvalpdf,"filled")
xline(tcrit,"--")
legend(["Student's t pdf","t-statistic", ...
    "Critical Cutoff"])

Figure contains an axes object. The axes object contains 3 objects of type line, scatter, constantline. These objects represent Student's t pdf, t-statistic, Critical Cutoff.

オレンジ色のドットは "t" 統計量を表し、棄却限界 "t" 値を表す黒い破線の左側にあります。

入力引数

すべて折りたたむ

標本データ。ベクトル、行列または多次元配列として指定します。ttest2 は NaN 値を欠損データとして扱い、それらのデータを無視します。

  • x および y がベクトルとして指定されている場合、同じ長さにする必要はありません。

  • x と y が行列として指定されている場合、これらの列数を同じにしなければなりません。この場合、ttest2 は t 検定を各列で別個に実行し、結果のベクトルを返します。

  • x と y が多次元配列として指定されている場合、それらのサイズは、大きさが 1 でない最初の次元を除くすべてに対して同じでなければなりません。

データ型: single | double

標本データ。ベクトル、行列または多次元配列として指定します。ttest2 は NaN 値を欠損データとして扱い、それらのデータを無視します。

  • x および y がベクトルとして指定されている場合、同じ長さにする必要はありません。

  • x と y が行列として指定されている場合、これらの列数を同じにしなければなりません。この場合、ttest2 は t 検定を各列で別個に実行し、結果のベクトルを返します。

  • x と y が多次元配列として指定されている場合、それらのサイズは、大きさが 1 でない最初の次元を除くすべてに対して同じでなければなりません。ttest2 は大きさが 1 でない最初の次元に対して機能します。

データ型: single | double

名前と値の引数

すべて折りたたむ

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: 'Tail','right','Alpha',0.01,'Vartype','unequal' は、有意水準 1% での右側検定を指定し、x と y の母集団分散は等しいと仮定しません。

仮説検定の有意水準。'Alpha' と、(0,1) の範囲内のスカラー値で構成されるコンマ区切りのペアとして指定します。

例: 'Alpha',0.01

データ型: single | double

平均を検定する入力行列の次元。'Dim' と正の整数値で構成されるコンマ区切りのペアとして指定します。たとえば、'Dim',1 を指定すると列の平均が検定され、'Dim',2 では行の平均が検定されます。

例: 'Dim',2

データ型: single | double

評価する対立仮説のタイプ。'Tail' と以下のいずれかで構成される、コンマ区切りのペアとして指定します。

  • 'both' — 母集団平均は等しくないという対立仮説を検定します。

  • 'right' — x の母集団平均は y の母集団平均よりも大きいという対立仮説を検定します。

  • 'left' — x の母集団平均は y の母集団平均よりも小さいという対立仮説を検定します。

ttest2 は、母集団平均は等しいという帰無仮説を、指定された対立仮説に対して検定します。

例: 'Tail','right'

分散タイプ。'Vartype' と、次のいずれかで構成されるコンマ区切りのペアとして指定します。

'equal'x と y は未知だが等しい分散の正規分布から派生しているという仮定を使用して検定を実行します。
'unequal'x と y は未知の等しくない分散の正規分布から派生しているという仮定を使用して検定を実行します。これは、ベーレンス・フィッシャー問題と呼ばれます。ttest2 は有効な自由度に対してサタースウェイト近似を使用します。

Vartype は単一の分散タイプでなければなりません。x が行列または多次元配列であっても同様です。

例: 'Vartype','unequal'

出力引数

すべて折りたたむ

1 または 0 として返される仮説検定の結果。

  • 値が 1 の場合、有意水準 Alpha で帰無仮説が棄却されます。

  • 値が 0 の場合、有意水準 Alpha では帰無仮説を棄却できません。

検定の p 値。[0,1] の範囲のスカラー値として返されます。p は、帰無仮説に基づく観測値と同様に、極端な検定統計量、またはより極端な検定統計量が観測される確率です。p の値が小さい場合、帰無仮説が有効でない可能性があります。

x と y の母集団平均の差に対する信頼区間。100 × (1 – Alpha)% の信頼区間の下限と上限を含む 2 要素ベクトルとして返されます。

2 標本 t 検定の検定統計量。以下を含む構造体として返されます。

  • tstat — 検定統計量の値。

  • df — 検定に対する自由度。

  • sd — 母標準偏差のプールされた推定値 (等しい分散の場合) または母集団標準偏差のプールされていない推定値を含むベクトル (異なる分散の場合)。

詳細

すべて折りたたむ

ヒント

  • sampsizepwr を使用して以下を計算します。

    • 指定された検出力およびパラメーター値に対応する標本サイズ

    • 真のパラメーター値が与えられた場合に特定の標本サイズに対して達成される検出力

    • 指定された標本サイズおよび検出力で検出できるパラメーター値

拡張機能

すべて展開する

バージョン履歴

R2006a より前に導入

参考

| |