極値分布
定義
位置パラメーター µ と スケール パラメーター σ をもつ極値分布に対する確率密度関数は、次の式で表されます。
この形式の確率密度関数は、最小値のモデル化に適しています。最大値のモデル化には元の値の負の値を使用してください。
T がパラメーター a と b をもつワイブル分布をもつ場合、log T はパラメーター µ = log a と σ = 1/b をもつ極値分布をもちます。
背景
極値分布の当てはめ
極値分布は、測定値や観測値を表す互いに独立で同一の分布に従う乱数の大きな集合における最小値あるいは最大値をモデリングするために使用されることが多くあります。極値分布は、裾が指数的に速く減衰する分布 (正規分布など) の最小値のモデル化に適しています。これは、また、元の値の負値を使用して、正規分布または指数分布などの分布からの最大値をモデル化できます。
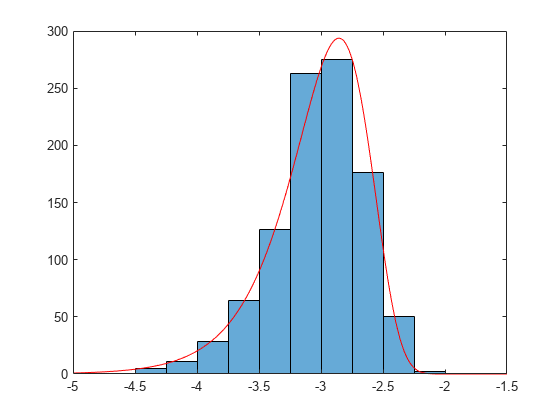
極値分布を正規分布の 500 回の観測からなる 1,000 セットで取られた最小値に当てはめます。
rng("default") % For reproducibility xMinima = min(randn(1000,500),[],2); paramEstsMinima = evfit(xMinima); y = linspace(-5,-1.5,1001); histogram(xMinima,-4.75:0.25:-1.75); p = evpdf(y,paramEstsMinima(1),paramEstsMinima(2)); line(y,0.25*length(xMinima)*p,"Color","red")
極値分布を観測の各セットの最大値に当てはめます。
rng("default") % For reproducibility xMaxima = max(randn(1000,500),[],2); paramEstsMaxima = evfit(-xMaxima); y = linspace(1.5,5,1001); histogram(xMaxima,1.75:0.25:4.75); p = evpdf(-y,paramEstsMaxima(1),paramEstsMaxima(2)); line(y,0.25*length(xMaxima)*p,"Color","red")

極値分布は、異常値のモデルとして最もよく使用されますが、他のタイプの連続データに対するモデルとしても使用できます。たとえば、極値分布は、ワイブル分布に緊密に関連しています。T がワイブル分布をもつ場合、log(T) は、タイプ 1 の極値分布をもちます。
パラメーター
関数 evfit は、極値分布の最尤推定とパラメーターの信頼区間を出力します。次の例は、近似した分布からの平均と分散の推定を含む、evfit を使用してある標本データを近似する方法を示します。
製造工程からの 1000 の各バッチで、最小のワッシャーのサイズをモデリングしたいとします。各バッチ内やバッチ間で、サイズが独立であると仮定すると、8 つの実験のバッチから最小径の測定の極値分布を近似することができます。次のコードは、分布パラメーターの最尤推定をparmhat に、信頼区間を parmci の列として出力します。
x = [19.774 20.141 19.44 20.511 21.377 19.003 19.66 18.83]; [parmhat, parmci] = evfit(x)
parmhat = 20.2506 0.8223 parmci = 19.644 0.49861 20.857 1.3562
関数 evstat を使用して、これらのパラメーターをもつ極値分布の平均と分散を求めることができます。
[meanfit, varfit] = evstat(parmhat(1),parmhat(2))
meanfit = 19.776 varfit = 1.1123
例
極値分布の確率密度関数の計算
極値分布の確率密度関数を計算します。
t = [-5:.01:2]; y = evpdf(t);
確率密度関数をプロットします。
figure; plot(t,y)

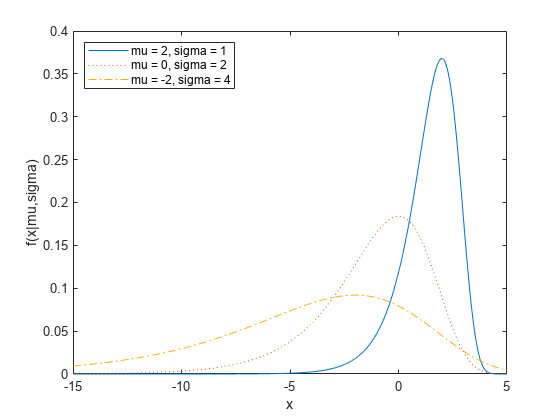
極値分布は左に歪んでおり、一般的な形はパラメーター値を変えても同じになります。位置パラメーター mu は実数直線に沿って分布を移動させ、スケール パラメーター sigma は分布を拡大または縮小します。
次の例では、mu と sigma の組み合わせを変えた場合について確率関数をプロットします。
x = -15:.01:5; plot(x,evpdf(x,2,1),'-', ... x,evpdf(x,0,2),':', ... x,evpdf(x,-2,4),'-.'); legend({'mu = 2, sigma = 1', ... 'mu = 0, sigma = 2', ... 'mu = -2, sigma = 4'}, ... 'Location','NW') xlabel('x') ylabel('f(x|mu,sigma)')