複数の分布近似の比較

この例では、複数の確率分布オブジェクトを同一の一連の標本データに当てはめ、各分布がデータにどの程度当てはまるかを視覚的に比較する方法を示します。

手順 1. 標本データを読み込みます。

標本データを読み込みます。

load carsmall

このデータには、さまざまな車種およびモデルのガロンあたりの走行マイル数 (MPG) の測定値が格納され、生産国 (Origin)、モデル年 (Model_Year)、その他の車両の特性によってグループ化されています。

手順 2. categorical 配列を作成します。

Origin を categorical 配列に変換し、標本データからイタリア車を削除します。イタリア車は 1 台しかないので、fitdist ではカーネル分布以外を使用してこのグループに分布を当てはめることはできません。

Origin = categorical(cellstr(Origin));
MPG2 = MPG(Origin~="Italy");
Origin2 = Origin(Origin~="Italy");
Origin2 = removecats(Origin2,"Italy");

手順 3. 複数の分布をグループ別に近似させます。

fitdist を使用し、ワイブル分布、正規分布、ロジスティック分布およびカーネル分布を MPG データの各生産国グループに近似します。

[WeiByOrig,Country] = fitdist(MPG2,"weibull","by",Origin2);
[NormByOrig,Country] = fitdist(MPG2,"normal","by",Origin2);
[LogByOrig,Country] = fitdist(MPG2,"logistic","by",Origin2);
[KerByOrig,Country] = fitdist(MPG2,"kernel","by",Origin2);

WeiByOrig

WeiByOrig=1×5 cell array
    {1×1 prob.WeibullDistribution}    {1×1 prob.WeibullDistribution}    {1×1 prob.WeibullDistribution}    {1×1 prob.WeibullDistribution}    {1×1 prob.WeibullDistribution}

Country

Country = 5×1 cell
    {'France' }
    {'Germany'}
    {'Japan'  }
    {'Sweden' }
    {'USA'    }

各国のグループに 4 つの分布オブジェクトが関連付けられました。たとえば、cell 配列 WeiByOrig には、標本データに示される各国に 1 つずつ、5 つのワイブル分布オブジェクトが含まれます。同様に、cell 配列 NormByOrig には 5 つの正規分布オブジェクトが含まれ、他も同様になります。各オブジェクトは、データ、分布およびパラメーターについての情報を保持するプロパティを含んでいます。配列 Country は、分布オブジェクトが cell 配列に格納されるのと同じ順番で各グループの生産国をリストします。

手順 4. 各分布の pdf を計算します。

米国の 4 つの確率分布オブジェクトを抽出し、各分布の pdf を計算します。手順 3 に示すように、米国は各 cell 配列の 5 番目の位置になります。

WeiUSA = WeiByOrig{5};
NormUSA = NormByOrig{5};
LogUSA = LogByOrig{5};
KerUSA = KerByOrig{5};

x = 0:1:50;
pdf_Wei = pdf(WeiUSA,x);
pdf_Norm = pdf(NormUSA,x);
pdf_Log = pdf(LogUSA,x);
pdf_Ker = pdf(KerUSA,x); 

手順 5. 各分布の pdf をプロットします。

標本データのヒストグラムに重ね合わせ、米国のデータに当てはめる各分布の pdf をプロットします。見やすいように、ヒストグラムを正規化します。

米国の標本データのヒストグラムを作成します。

data = MPG(Origin2=="USA");
figure
histogram(data,10,Normalization="pdf",FaceAlpha=0.4);

当てはめた各分布の確率密度関数をプロットします。

line(x,pdf_Wei,LineStyle="-",LineWidth=1)
line(x,pdf_Norm,LineStyle="-.",LineWidth=1)
line(x,pdf_Log,LineStyle="--",LineWidth=1)
line(x,pdf_Ker,LineStyle=":",LineWidth=1)
legend("Data","Weibull","Normal","Logistic","Kernel","Location","Best")
title("MPG for Cars from USA")
xlabel("MPG")

標本データのヒストグラムに確率密度関数プロットを重ね合わせると、各種の分布がデータをどの程度近似できるのかを視覚的に比較できるようになります。ノンパラメトリックなカーネル分布 KerUSA のみが、元のデータの 2 つの最頻値をほぼ明確にしています。

手順 6. 米国データを年別にさらにグループ化します。

手順 5 で明確になった 2 つの最頻値を調査するには、MPG データを生産国 (Origin) とモデル年 (Model_Year) の両方でグループ化し、fitdist を使用してカーネル分布を各グループに近似します。

[KerByYearOrig,Names] = fitdist(MPG,"Kernel","By",{Origin Model_Year});

生産国とモデル年の固有の各組み合わせには、カーネル分布オブジェクトが関連付けられました。

Names

Names = 14×1 cell
    {'France↵70' }
    {'France↵76' }
    {'Germany↵70'}
    {'Germany↵76'}
    {'Germany↵82'}
    {'Italy↵76'  }
    {'Japan↵70'  }
    {'Japan↵76'  }
    {'Japan↵82'  }
    {'Sweden↵70' }
    {'Sweden↵76' }
    {'USA↵70'    }
    {'USA↵76'    }
    {'USA↵82'    }

米国の各モデル年について 3 つの確率分布をプロットします。これらは、cell 配列 KerByYearOrig の 12、13 および 14 の位置にあります。

figure
hold on
for i = 12 : 14
    plot(x,pdf(KerByYearOrig{i},x))
end
legend("1970","1976","1982")
title("MPG in USA Cars by Model Year")
xlabel("MPG")
hold off

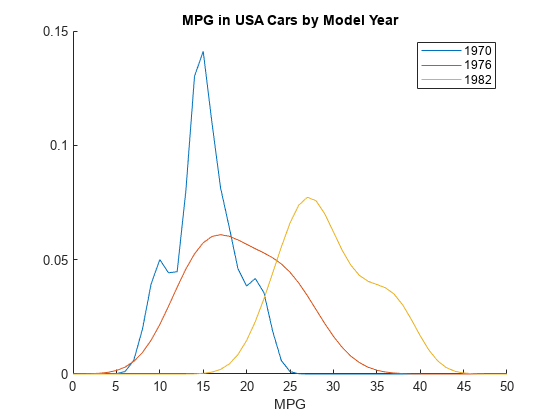
モデル年別にさらにグループ化すると、米国で生産された車の MPG データには、2 つの明確なピークが存在することが確率密度関数のプロットからわかります。1 つはモデル年 1970、もう 1 つはモデル年 1982 です。これにより、米国のガロンあたりの走行マイル数データを組み合わせたヒストグラムに 1 つではなく 2 つのピークがある理由がわかります。

参考

fitdist | pdf | histogram

トピック

• グループ化変数
• 確率分布オブジェクトのグループ化されたデータへの当てはめ
• 確率分布の操作
• サポートされている分布