レイリー分布

定義

x ≥ 0 のレイリー pdf は次のようになります。

$$y=f(x|b)=\frac{x}{b^2}{e}^{\left(\frac{-x^2}{2b^2}\right)}$$

背景

レイリー分布は、ワイブル分布の特別な場合です。A と B がワイブル分布のパラメーターである場合、パラメーター b をもつレイリー分布はパラメーター $$A=\sqrt{2}b$$ および B = 2 のワイブル分布と等価になります。

x 方向と y 方向での粒子の速度が、平均が 0 で互いに等しい分散をもつ 2 つの独立した正規分布からの確率変数の場合、それぞれの時間ごとに移動する距離はレイリー分布に従います。

通信理論では、多重経路で受信機に到達する散乱信号のモデル化に、仲上分布、ライス分布、レイリー分布が使用されます。散乱の密度に依存して、信号は異なるフェージングの特性を示します。レイリー分布と仲上分布は、散乱密度が強い場合の散乱信号のモデル化に使用されます。一方、ライス分布は、見通し距離内通信の信号が強い場合のフェージングをモデル化します。仲上分布は、レイリー分布を拡張したもので、フェージングの範囲を詳細に制御できます。

パラメーター

関数 raylfit は、レイリー分布のパラメーターの最尤推定値を返します。この推定は、以下のとおりです。

$$b=\sqrt{\frac{1}{2n}{\displaystyle \sum _{i=1}^n{x}_i^2}}$$

例

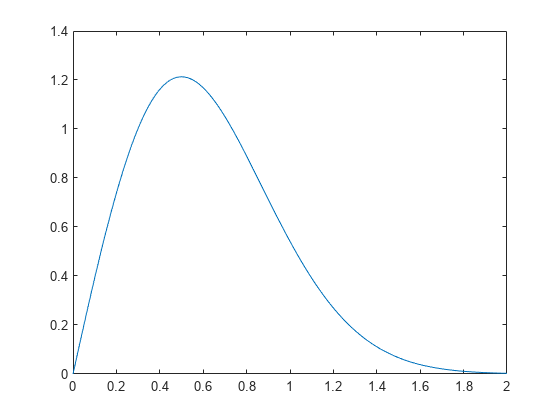
レイリー確率密度関数の計算とプロット

x=0 から x=2 までの値について、スケール パラメーターが b=0.5 のレイリー確率密度関数 (pdf) を計算します。

x = 0:0.01:2;
p = raylpdf(x,0.5);

確率密度関数をプロットします。

figure;
plot(x,p)
grid on
xlabel("x")
ylabel("p")

参考

RayleighDistribution

トピック

• 確率分布の操作
• サポートされている分布