カスタム分布の当てはめ

0 を打ち切ったポアソン分布の当てはめ

ほとんどの場合、カウント データはポアソン分布を使用してモデル化されます。関数 poissfit または fitdist を使用して、ポアソン分布を当てはめることができます。しかし、0 であるカウントはデータに記録されず、0 の欠損のためにポアソン分布を当てはめるのが難しい場合があります。その場合、関数 mle およびカスタム分布関数を使用して、0 を打ち切ったデータにポアソン分布を当てはめます。

最初に、ランダムなポアソン データを生成します。

rng(18,'twister') % For reproducibility
lambda = 1.75;
n = 75;
x1 = poissrnd(lambda,n,1);

次に、打ち切りをシミュレートするデータから 0 をすべて削除します。

x1 = x1(x1 > 0);

打ち切りの後、x1 の標本数をチェックします。

length(x1)

ans = 
65

シミュレーション データのヒストグラムをプロットします。

histogram(x1,0:1:max(x1)+1)

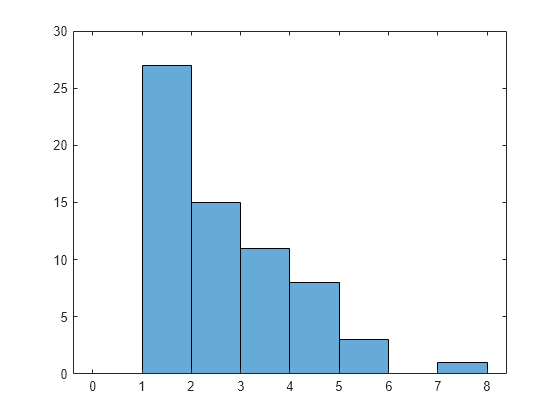
データは、0 がないこと以外はポアソン分布のように見えます。正の整数ではポアソン分布と一致し、0 では確率のないカスタム分布を使用できます。カスタム分布を使用すると、0 の欠損を考慮しながら、ポアソン分布のパラメーター lambda を推定できます。

0 を打ち切ったポアソン分布は、その確率質量関数 (pmf) で定義する必要があります。ポアソン分布の平均のパラメーター lambda の値を指定して、x1 の各点の確率を計算する無名関数を作成します。0 を打ち切ったポアソン分布の pmf は、和が 1 になるように正規化されたポアソン pmf です。0 を打ち切ると、正規化は 1–Probability(x1<0) です。

pf_truncpoiss = @(x1,lambda) poisspdf(x1,lambda)./(1-poisscdf(0,lambda));

簡略化するために、この関数に与えられるすべての x1 値は正の整数で、チェックを行わないとします。エラー チェックの場合、または複数行のコードを要するさらに複雑な分布の場合は、関数を別のファイルで定義する必要があります。

パラメーター lambda に対し、適切なおおよその初期推定値を見つけます。ここでは、標本平均を使用します。

start = mean(x1)

start = 
2.2154

mle にデータ、カスタム pmf 関数、初期パラメーター値、およびパラメーターの下限を提供します。ポアソン分布の平均パラメーターは正でなければならないため、lambda の下限も指定する必要があります。関数 mle は、lambda の最尤推定と、オプションとしてパラメーターの近似した 95% 信頼区間を出力します。

[lambdaHat,lambdaCI] = mle(x1,'pdf',pf_truncpoiss,'Start',start, ...
    'LowerBound',0)

lambdaHat = 
1.8760

lambdaCI = 2×1

    1.4990
    2.2530

パラメーターの推定値は、標本平均より小さくなっています。最尤推定ではデータに存在しない 0 を考慮します。

代わりに、名前と値の引数 TruncationBounds を使用して、打ち切りの範囲を指定できます。

[lambdaHat2,lambdaCI2] = mle(x1,'Distribution','Poisson', ...
    'TruncationBounds',[0 Inf])

lambdaHat2 = 
1.8760

lambdaCI2 = 2×1

    1.4990
    2.2530

また、mlecov が返す大きい標本の分散の近似を使用して、lambda の標準誤差推定も計算できます。

avar = mlecov(lambdaHat,x1,'pdf',pf_truncpoiss);
stderr = sqrt(avar)

stderr = 
0.1923

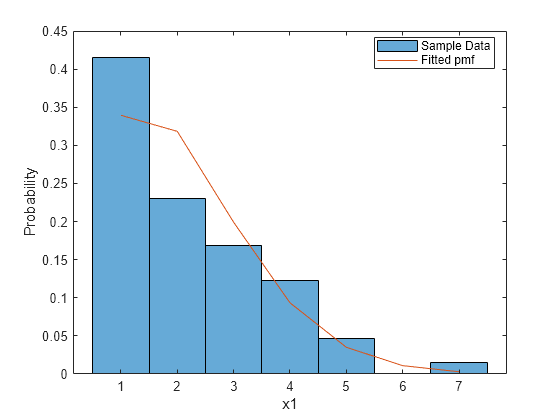
視覚的に当てはめをチェックするために、生データの正規化ヒストグラムに対して当てはめられた pmf をプロットします。

histogram(x1,'Normalization','pdf')
xgrid = min(x1):max(x1);
pmfgrid = pf_truncpoiss(xgrid,lambdaHat);
hold on
plot(xgrid,pmfgrid,'-')
xlabel('x1')
ylabel('Probability')
legend('Sample Data','Fitted pmf','Location','best')
hold off

上限を打ち切った正規分布の当てはめ

連続データは打ち切られている場合があります。たとえば、データ収集の制限のため、所定の固定値より大きい観測値が記録されない場合があります。

その場合、打ち切り処理を行った正規分布のデータのシミュレーションを行います。最初に、無作為な正規データを生成します。

n = 500;
mu = 1;
sigma = 3;
rng('default') % For reproducibility
x2 = normrnd(mu,sigma,n,1);

次に、打ち切り点 xTrunc を超える観測値を削除します。xTrunc は推定する必要がない既知の値であると仮定します。

xTrunc = 4;
x2 = x2(x2 < xTrunc);

打ち切りの後、x2 の標本数をチェックします。

length(x2)

ans = 
430

シミュレーション データのヒストグラムを作成します。

histogram(x2)

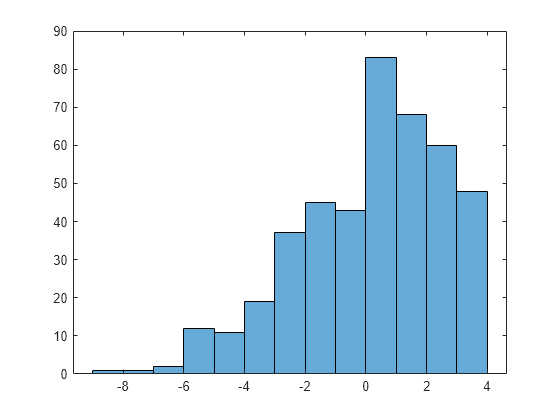
x2 < xTrunc では正規分布と一致し、xTrunc を超えると 0 確率となるカスタム分布で、シミュレーション データを当てはめます。カスタム分布を使用すると、裾の欠損を考慮しながら、正規分布のパラメーター mu および sigma を推定できます。

打ち切り処理を行った正規分布を、その pdf で定義します。パラメーター mu および sigma の値を指定して、x の各点の確率密度値を計算する無名関数を作成します。打ち切り点は固定かつ既知であり、打ち切られた正規分布の pdf は、打ち切った後に積分が 1 となるよう正規化された pdf です。正規化は xTrunc で評価された cdf です。簡略化するために、すべての x2 値は xTrunc より小さく、チェックを行わないとします。

pdf_truncnorm = @(x2,mu,sigma) ...
    normpdf(x2,mu,sigma)./normcdf(xTrunc,mu,sigma);

打ち切り点 xTrunc は推定する必要がないため、カスタム pdf 関数の入力分布パラメーターに含まれません。また、xTrunc はデータ ベクトル入力引数の一部ではありません。無名関数はワークスペース内の変数にアクセスできるので、xTrunc を無名関数に追加の引数として渡す必要がありません。

パラメーター推定としておおよその初期推定値を指定します。この場合、打ち切りが極端でないため、標本平均と標準偏差を使用します。

start = [mean(x2),std(x2)]

start = 1×2

    0.1585    2.4125

mle にデータ、カスタム pdf 関数、初期パラメーター値、およびパラメーターの下限を提供します。sigma は正でなければならないため、パラメーターの下限も指定する必要があります。mle は単一ベクトルとして mu および sigma の最尤推定、およびこの 2 つのパラメーターについて約 95% の信頼区間の行列を返します。

[paramEsts,paramCIs] = mle(x2,'pdf',pdf_truncnorm,'Start',start, ...
    'LowerBound',[-Inf 0])

paramEsts = 1×2

    1.1298    3.0884

paramCIs = 2×2

    0.5713    2.7160
    1.6882    3.4607

mu および sigma の推定値が標本平均および標準偏差より大きくなっています。モデルの当てはめは分布の欠損した上裾を考慮しています。

代わりに、名前と値の引数 TruncationBounds を使用して、打ち切りの範囲を指定できます。

[paramEsts2,paramCIs2] = mle(x2,'Distribution','Normal', ...
    'TruncationBounds',[-Inf xTrunc])

paramEsts2 = 1×2

    1.1297    3.0884

paramCIs2 = 2×2

    0.5713    2.7160
    1.6882    3.4607

mlecov を使用して、パラメーター推定の近似共分散行列を計算できます。通常、近似は標本が大きい場合に良好に機能するので、標準誤差は対角要素の平方根で概算できます。

acov = mlecov(paramEsts,x2,'pdf',pdf_truncnorm)

acov = 2×2

    0.0812    0.0402
    0.0402    0.0361

stderr = sqrt(diag(acov))

stderr = 2×1

    0.2849
    0.1900

視覚的に当てはめをチェックするために、生データの正規化ヒストグラムに対して当てはめた pdf をプロットします。

histogram(x2,'Normalization','pdf')
xgrid = linspace(min(x2),max(x2));
pdfgrid = pdf_truncnorm(xgrid,paramEsts(1),paramEsts(2));
hold on
plot(xgrid,pdfgrid,'-')
xlabel('x2')
ylabel('Probability Density')
legend('Sample Data','Fitted pdf','Location','best')
hold off

2 つの正規分布から成る混合の当てはめ

データ セットには二峰性または多峰性を示すものがありますが、そのようなデータに標準分布を当てはめるのは多くの場合不適切です。ただし、単純な単峰性分布を混合することで、このようなデータをモデル化できることがよくあります。

この場合、2 つの正規分布を混合したものをシミュレーションを行ったデータに当てはめます。次の構造的定義をもつシミュレーション データを考えます。

当てはめているものと同じモデルを使用するのではなく、スチューデントの "t" 分布の混合からデータ セットを生成します。異なる分布を使用することで、モンテカルロ シミュレーションで使用される手法と同様に、当てはめられているモデルの仮定からの逸脱に対して、当てはめ手法がどの程度ロバストであるかについて検定できます。

rng(10) % For reproducibility
x3 = [trnd(20,1,50) trnd(4,1,100)+3];
histogram(x3)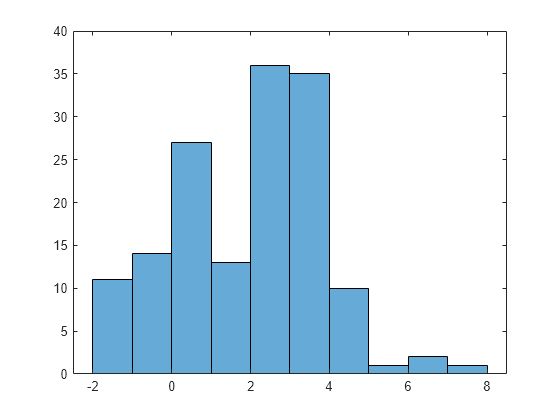

確率密度を計算する無名関数を作成することにより、当てはめるモデルを定義します。2 つの正規分布を混合した pdf は 2 つの正規成分の pdf の重み付き和であり、混合の確率で重み付けられます。この無名関数には、pdf を評価するデータのベクトル、および 5 つの分布パラメーターという 6 つの入力引数があります。各成分にはその平均および標準偏差のパラメーターがあります。

pdf_normmixture = @(x3,p,mu1,mu2,sigma1,sigma2) ...
    p*normpdf(x3,mu1,sigma1) + (1-p)*normpdf(x3,mu2,sigma2);

また、パラメーターの初期推定値も必要です。モデル パラメーターの数が増加するにつれて、開始点の定義がより重要になります。ここでは、データの 2 つの四分位点を中心とした、等しい標準偏差をもつ、正規分布の等量混合 (p = 0.5) から開始します。標準偏差の開始値は、各成分の平均および分散として、混合の分散式から生成されます。

pStart = .5;
muStart = quantile(x3,[.25 .75])

muStart = 1×2

    0.3351    3.3046

sigmaStart = sqrt(var(x3) - .25*diff(muStart).^2)

sigmaStart = 
1.1602

start = [pStart muStart sigmaStart sigmaStart];

混合の確率に対する 0 と 1 の境界、および標準偏差の 0 の下限を指定します。範囲ベクトルの残りの要素は +Inf または –Inf に設定し、制限がないことを示します。

lb = [0 -Inf -Inf 0 0];
ub = [1 Inf Inf Inf Inf];
paramEsts = mle(x3,'pdf',pdf_normmixture,'Start',start, ...
    'LowerBound',lb,'UpperBound',ub)

Warning: Maximum likelihood estimation did not converge.  Iteration limit exceeded.

paramEsts = 1×5

    0.3273   -0.2263    2.9914    0.9067    1.2059

警告メッセージは、この関数が既定の反復設定では収束しないことを示しています。既定のオプションを表示します。

statset('mlecustom')

ans = struct with fields:
          Display: 'off'
      MaxFunEvals: 400
          MaxIter: 200
           TolBnd: 1.0000e-06
           TolFun: 1.0000e-06
       TolTypeFun: []
             TolX: 1.0000e-06
         TolTypeX: []
          GradObj: 'off'
         Jacobian: []
        DerivStep: 6.0555e-06
      FunValCheck: 'on'
           Robust: []
     RobustWgtFun: []
           WgtFun: []
             Tune: []
      UseParallel: []
    UseSubstreams: []
          Streams: {}
        OutputFcn: []

カスタム分布に対する既定の最大反復回数は 200 です。関数 statset で作成したオプション構造体を使用し、この既定値をオーバーライドして反復回数を増やします。また、最大関数評価を増やします。

options = statset('MaxIter',300,'MaxFunEvals',600);
paramEsts = mle(x3,'pdf',pdf_normmixture,'Start',start, ...
    'LowerBound',lb,'UpperBound',ub,'Options',options)

paramEsts = 1×5

    0.3273   -0.2263    2.9914    0.9067    1.2059

収束の最終的な反復は、結果の最後の数桁にしか関係ありません。ただし、収束に達していることを必ず確認することをお勧めします。

視覚的に当てはめをチェックするために、生データの確率のヒストグラムに対して当てはめた密度をプロットします。

histogram(x3,'Normalization','pdf')
hold on
xgrid = linspace(1.1*min(x3),1.1*max(x3),200);
pdfgrid = pdf_normmixture(xgrid, ...
    paramEsts(1),paramEsts(2),paramEsts(3),paramEsts(4),paramEsts(5));
plot(xgrid,pdfgrid,'-')
hold off
xlabel('x3')
ylabel('Probability Density')
legend('Sample Data','Fitted pdf','Location','best')

代わりに、正規分布の混合には関数 fitgmdist を使用できます。初期推定および反復アルゴリズムの設定により、推定値が異なる場合があります。

Mdl = fitgmdist(x3',2)

Mdl = 

Gaussian mixture distribution with 2 components in 1 dimensions
Component 1:
Mixing proportion: 0.329180
Mean:   -0.2200

Component 2:
Mixing proportion: 0.670820
Mean:    2.9975

Mdl.Sigma

ans = 
ans(:,:,1) =

    0.8274


ans(:,:,2) =

    1.4437

精度が異なるデータへの重み付き正規分布の当てはめ

10 個のデータ点があり、それぞれが 1 ～ 8 個の観測値のいずれかの平均であるとします。元の観測値は利用できませんが、各データ点の観測値の個数は既知です。各ポイントの精度は、対応する観測値の個数によって異なります。生データの平均値と標準偏差を推定する必要があります。

x4 = [0.25 -1.24 1.38 1.39 -1.43 2.79 3.52 0.92 1.44 1.26]';
m = [8 2 1 3 8 4 2 5 2 4]';

各データ点の分散は対応する観測値の個数に反比例するため、1/m を使用して最尤近似の各データ点の分散を重み付けします。

w = 1./m;

このモデルでは、分布はその pdf で定義できます。ただし、正規 pdf は次の形式のため、pdf の対数を使用する方がより適切です。

  c .* exp(-0.5 .* z.^2),

また、mle は pdf の対数を取り、対数尤度を計算します。したがって、代わりに pdf の対数を直接計算する関数を作成します。

関数 pdf の対数は、正規分布のパラメーター mu および sigma の値を指定して、x の各点に対する確率密度の対数を計算する必要があります。また、別の分散の重みを考慮する必要もあります。helper_logpdf_wn1 という名前の関数を別のファイル helper_logpdf_wn1.m に定義します。

function logy = helper_logpdf_wn1(x,m,mu,sigma)
%HELPER_LOGPDF_WN1 Logarithm of pdf for a weight normal distribution
% This function supports only the example Fit Custom Distributions 
% (customdist1demo.mlx) and might change in a future release.
v = sigma.^2 ./ m;
logy = -(x-mu).^2 ./ (2.*v) - .5.*log(2.*pi.*v);
end

パラメーター推定のおおよその初期推定値を指定します。この場合、重み付けされていない標本平均と標準偏差を使用します。

start = [mean(x4),std(x4)]

start = 1×2

    1.0280    1.5490

sigma は正でなければならないため、パラメーターの下限を指定する必要があります。

[paramEsts1,paramCIs1] = mle(x4,'logpdf', ...
    @(x,mu,sigma)helper_logpdf_wn1(x,m,mu,sigma), ...
    'Start',start,'LowerBound',[-Inf,0])

paramEsts1 = 1×2

    0.6244    2.8823

paramCIs1 = 2×2

   -0.2802    1.6191
    1.5290    4.1456

mu の推定値は標本平均の推定値の 3 分の 2 未満です。推定値に影響を与えるのは、最も信頼性の高いデータ点、つまり最も多い生の観測値に基づくデータ点です。このデータ セットでは、これらの点が重み付けされていない標本平均から推定値を引き下げる傾向にあります。

パラメーター変換を使用した正規分布の当てはめ

関数 mle は、厳密法が利用できない場合、推定器の分布について、大きい標本の正規近似を使用してパラメーターの信頼区間を計算します。標本サイズが小さい場合は、1 つ以上のパラメーターを変換することにより正規近似を改良できます。この場合、正規分布のスケール パラメーターを対数に変換します。

最初に、変換されたパラメーターを sigma に使用する helper_logpdf_wn2 という名前の新しい対数関数 pdf を作成します。

function logy = helper_logpdf_wn2(x,m,mu,logsigma)
%HELPER_LOGPDF_WN2 Logarithm of pdf for a weight normal distribution with 
% log(sigma) parameterization
% This function supports only the example Fit Custom Distributions 
% (customdist1demo.mlx) and might change in a future release.
v = exp(logsigma).^2 ./ m;
logy = -(x-mu).^2 ./ (2.*v) - .5.*log(2.*pi.*v);
end

sigma の新しいパラメーター化に変換された同じ開始点、つまり、標本標準偏差の対数を使用します。

start = [mean(x4),log(std(x4))]

start = 1×2

    1.0280    0.4376

sigma は任意の正の値であるため、log(sigma) は非有界であり、下限や上限を指定する必要はありません。

[paramEsts2,paramCIs2] = mle(x4,'logpdf', ...
    @(x,mu,sigma)helper_logpdf_wn2(x,m,mu,sigma), ...
    'Start',start)

paramEsts2 = 1×2

    0.6244    1.0586

paramCIs2 = 2×2

   -0.2802    0.6203
    1.5290    1.4969

パラメーター化では log(sigma) が使用されるため、変換してオリジナルのスケールに戻し、sigma の推定値と信頼区間を取得する必要があります。

sigmaHat = exp(paramEsts2(2))

sigmaHat = 
2.8823

sigmaCI = exp(paramCIs2(:,2))

sigmaCI = 2×1

    1.8596
    4.4677

最尤推定がパラメーター化に対し不変であるため、mu および sigma 両方の推定値は最初の当てはめと同じです。sigma に対する信頼区間は paramCIs1(:,2) とは少し異なります。