Main Content

最尤推定法

ライブ スクリプトを開く

関数 mle は、名前によって指定された分布、および確率密度関数 (pdf)、対数 pdf または負の対数尤度関数によって指定されたカスタム分布について、最尤推定量 (MLE) を計算します。

一部の分布では、MLE を閉形式で与えて直接計算することができます。他の分布では、最尤推定量を求める必要があります。この探索は、関数 statset を使用して作成される入力引数 options で調節できます。効果的な探索には、適当な分布モデルを選択し、適切な収束判定値を設定することが重要です。

MLE は、小さい標本の場合は特に、偏ることがあります。しかし、標本のサイズが大きくなるにつれて、MLE は漸近正規分布に従う最小分散不偏推定量になります。これは、推定の信頼限界を計算するために使用されます。

たとえば、指数分布の繰り返し無作為標本から得られた平均をもつ次の分布を考えます。

mu = 1; % Population parameter
n = 1e3; % Sample size
ns = 1e4; % Number of samples

rng('default')  % For reproducibility
samples = exprnd(mu,n,ns); % Population samples
means = mean(samples); % Sample means

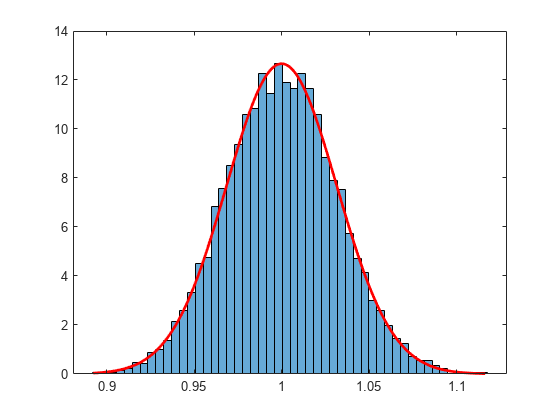
中心極限定理によると、標本データの分布にかかわらず、平均はほぼ正規分布に従います。関数 mle を使用すると、平均に最もよく当てはまる正規分布を求めることができます。

[phat,pci] = mle(means)
phat = 1×2

    1.0000    0.0315


pci = 2×2

    0.9994    0.0311
    1.0006    0.0319

phat(1) と phat(2) は平均と標準偏差の MLE です。pci(:,1) と pci(:,1) は対応する 95% 信頼区間です。

当てはめた正規分布とともに標本平均の分布を可視化します。

numbins = 50;
histogram(means,numbins,'Normalization','pdf')
hold on
x = min(means):0.001:max(means);
y = normpdf(x,phat(1),phat(2));
plot(x,y,'r','LineWidth',2)

Figure contains an axes object. The axes object contains 2 objects of type histogram, line.

参考

|

関連する例

詳細