一様分布 (連続)
概要
一様分布 (矩形分布と呼ばれる場合もあります) は、2 パラメーターの曲線群です。2 つの境界パラメーター間に一定の確率分布関数 (pdf) が存在することで知られています。この分布は、小数点部分を特定の桁数にそろえたときの値における丸め誤差の分布を表すのに適しています。一様分布は、逆関数法などの乱数発生法で使われます。
Statistics and Machine Learning Toolbox™ には、一様分布を処理する方法がいくつか用意されています。
パラメーター
一様分布は、次のパラメーターを使用します。
| パラメーター | 説明 | サポート |
|---|---|---|
a | 下限端点 | -∞ < a < b |
b | 上限端点 | a < b < ∞ |
標準一様分布では、a = 0 および b = 1 です。
パラメーター推定
"最尤推定量" (MLE) は、尤度関数が最大になるパラメーター推定値です。一様分布の a と b の最尤推定量は、それぞれ、標本の最小値と最大値です。
確率密度関数
一様分布の確率密度関数は次のようになります。
確率密度関数では、a と b の間が一定です。
たとえば、連続一様分布の確率密度関数の計算を参照してください。
累積分布関数
一様分布の累積分布関数 (cdf) は次のようになります。
結果 p は、パラメーター a および b をもつ一様分布に従う単一の観測値が区間 [a x] に含まれる確率です。
たとえば、連続一様分布の累積分布関数の計算を参照してください。
記述統計
一様分布の平均は です。
一様分布の分散は です。
乱数発生
標準一様分布を使用すると、逆関数法を使用して他の任意の連続分布に従う乱数を生成できます。逆関数法は、連続累積分布関数 (cdf) は開区間 (0, 1) 全体にまたがって一意に分布するという原則に依存しています。u が (0, 1) の一様な乱数である場合、x = F–1(u) は、指定された累積分布関数 F に従う連続分布から乱数 x を生成します。
たとえば、一様分布の逆関数を使用した乱数の生成を参照してください。
例
連続一様分布の確率密度関数の計算
パラメーターが異なる 3 つの一様分布オブジェクトを作成します。
pd1 = makedist('Uniform'); % Standard uniform distribution pd2 = makedist('Uniform','lower',-2,'upper',2); % Uniform distribution with a = -2 and b = 2 pd3 = makedist('Uniform','lower',-2,'upper',1); % Uniform distribution with a = -2 and b = 1
3 つの一様分布の pdf を計算します。
x = -3:.01:3; pdf1 = pdf(pd1,x); pdf2 = pdf(pd2,x); pdf3 = pdf(pd3,x);
同じ軸に pdf をプロットします。
figure; plot(x,pdf1,'r','LineWidth',2); hold on; plot(x,pdf2,'k:','LineWidth',2); plot(x,pdf3,'b-.','LineWidth',2); legend({'a = 0, b = 1','a = -2, b = 2','a = -2, b = 1'},'Location','northwest'); xlabel('Observation') ylabel('Probability Density') hold off;
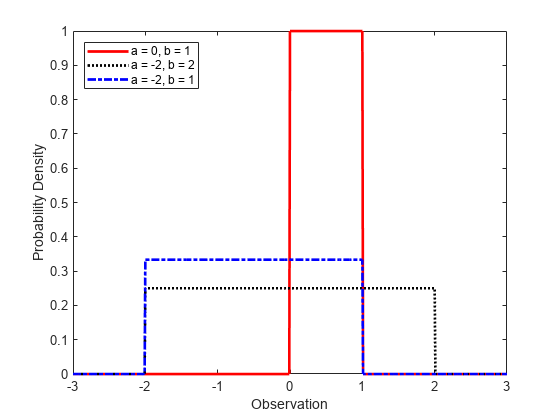
区間 (a,b) の幅が増加すると、各 pdf の高さが減少します。
連続一様分布の累積分布関数の計算
パラメーターが異なる 3 つの一様分布オブジェクトを作成します。
pd1 = makedist('Uniform'); % Standard uniform distribution pd2 = makedist('Uniform','lower',-2,'upper',2); % Uniform distribution with a = -2 and b = 2 pd3 = makedist('Uniform','lower',-2,'upper',1); % Uniform distribution with a = -2 and b = 1
3 つの一様分布の cdf を計算します。
x = -3:.01:3; cdf1 = cdf(pd1,x); cdf2 = cdf(pd2,x); cdf3 = cdf(pd3,x);
同じ軸に cdf をプロットします。
figure; plot(x,cdf1,'r','LineWidth',2); hold on; plot(x,cdf2,'k:','LineWidth',2); plot(x,cdf3,'b-.','LineWidth',2); legend({'a = 0, b = 1','a = -2, b = 2','a = -2, b = 1'},'Location','NW'); xlabel('Observation') ylabel('Cumulative Probability') hold off;

区間 (a,b) の幅が増加すると、各 cdf の傾きが減少します。
関連する分布
参照
[1] Abramowitz, Milton, and Irene A. Stegun, eds. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. 9. Dover print.; [Nachdr. der Ausg. von 1972]. Dover Books on Mathematics. New York, NY: Dover Publ, 2013.
[2] Devroye, Luc. Non-Uniform Random Variate Generation. New York, NY: Springer New York, 1986. https://doi.org/10.1007/978-1-4613-8643-8
[3] Evans, Merran, Nicholas Hastings, and Brian Peacock. Statistical Distributions. 2nd ed. New York: J. Wiley, 1993.
参考
UniformDistribution | unifcdf | unifpdf | unifinv | unifit | unifstat | unifrnd | makedist | fitdist