三角分布

R2026a

概要

三角分布は、使用できる標本データが制限されている場合に、確率分布の単純化された表現を提供します。パラメーターは、データの最小値、最大値およびピークです。一般的な応用例として、ビジネスや経済のシミュレーション、プロジェクト管理の計画、自然現象のモデル化、オーディオのディザリングなどがあります。

パラメーター

三角分布は、次のパラメーターを使用します。

パラメーター	説明	制約
`a`	下限	$A \leq B$
`b`	ピークの位置	$A \leq B \leq C$
`c`	上限	$C \geq B$

三角分布の平均と分散は、a、b および c の各パラメーターに関連しています。

平均は、以下のとおりです。

$mean = (\frac{a + b + c}{3}) .$

分散は、以下のとおりです。

$var = (\frac{a^{2} + b^{2} + c^{2} - a b - a c - b c}{18}) .$

パラメーター推定

通常、標本データに基づき、客観的で妥当な値を使用して、三角分布パラメーターを推定します。標本データの最小値と最大値を使って、それぞれ下限パラメーターと上限パラメーター a と c を推定できます。標本の平均、ラジアン、最頻値または他の客観的に合理性がある母集団の最頻値の推定を使って、ピーク位置パラメーター b を推定できます。

確率密度関数

対数正規分布の確率密度関数 (pdf) は、以下のとおりです。

$f (x | a, b, c) = {\begin{matrix} \frac{2 (x - a)}{(c - a) (b - a)}; a \leq x \leq b \\ \frac{2 (c - x)}{(c - a) (c - b)}; b < x \leq c \\ 0; x < a, x > c \end{matrix} .$

例については、三角分布の確率分布関数のプロットを参照してください。

累積分布関数

三角分布の累積分布関数 (cdf) は、です。

$F (x | a, b, c) = {\begin{matrix} 0, x < a \\ \frac{{(x - a)}^{2}}{(c - a) (b - a)}, a \leq x \leq b \\ 1 - \frac{{(c - x)}^{2}}{(c - a) (c - b)}, b < x \leq c \\ 1, x > c \end{matrix} .$

例については、三角分布の累積分布関数のプロットを参照してください。

例

三角分布の確率分布関数のプロット

ライブスクリプトを開く

三角分布のパラメーター "a"、"b"、"c" の値を変更して、確率分布関数 (pdf) の形状に変化を加えます。

パラメーターの値が異なる 4 つの三角分布オブジェクトを作成します。

pd1 = makedist("Triangular");
pd2 = makedist("Triangular","a",-1,"b",0,"c",1);
pd3 = makedist("Triangular","a",-0.5,"b",0,"c",1);
pd4 = makedist("Triangular","a",0,"b",0,"c",1);

4 つの分布の確率分布関数を計算します。

x = -2:0.01:2;
pdf1 = pdf(pd1,x);
pdf2 = pdf(pd2,x);
pdf3 = pdf(pd3,x);
pdf4 = pdf(pd4,x);

4 つの確率分布関数をプロットします。

plot(x,pdf1)
hold on
plot(x,pdf2,":")
plot(x,pdf3,"-.")
plot(x,pdf4,"--")
legend(["a = 0, b = 0.5, c = 1","a = -1, b = 0, c = 1", ...
    "a = -0.5, b = 0, c = 1","a = 0, b = 0, c = 1"], ...
    "Location","northwest");
hold off

Figure contains an axes object. The axes object contains 4 objects of type line. These objects represent a = 0, b = 0.5, c = 1, a = -1, b = 0, c = 1, a = -0.5, b = 0, c = 1, a = 0, b = 0, c = 1.

"a" と "c" の間の距離が大きくなるにつれて、分布境界内の特定の値における密度は低下します。密度関数は積分されて 1 になるため、幅が増加するにつれて確率密度関数のプロットの高さは低下します。ピークパラメーター "b" の位置によって、確率分布関数が右または左に歪むかどうかや、対称形となるかどうかが決まります。

三角分布の累積分布関数のプロット

ライブスクリプトを開く

三角分布のパラメーター "a"、"b"、"c" の値を変更して、累積分布関数 (cdf) の形状に変化を加えます。

パラメーターが異なる 4 つの三角分布オブジェクトを作成します。

pd1 = makedist("Triangular");
pd2 = makedist("Triangular","a",-1,"b",0,"c",1);
pd3 = makedist("Triangular","a",-0.5,"b",0,"c",1);
pd4 = makedist("Triangular","a",0,"b",0,"c",1);

4 つの分布の累積分布関数を計算します。

x = -1.2:0.01:1.2;
cdf1 = cdf(pd1,x);
cdf2 = cdf(pd2,x);
cdf3 = cdf(pd3,x);
cdf4 = cdf(pd4,x);

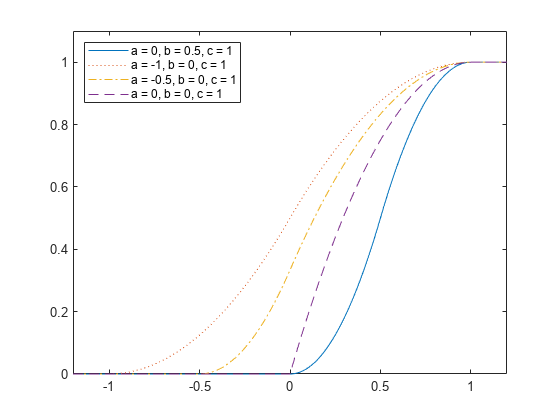
4 つの累積分布関数をプロットします。

plot(x,cdf1)
hold on
plot(x,cdf2,":")
plot(x,cdf3,"-.")
plot(x,cdf4,"--")
legend(["a = 0, b = 0.5, c = 1","a = -1, b = 0, c = 1", ...
    "a = -0.5, b = 0, c = 1","a = 0, b = 0, c = 1"], ...
    "Location","northwest");
xlim([-1.2 1.2]);
ylim([0 1.1])
hold off