対数正規分布
概要
対数正規分布 (Galton 分布と呼ばれることもあります) は、対数が正規分布に従う確率分布です。log(x) が存在するのは x が正である場合だけなので、対数正規分布は対象となる数量が必ず正である場合に適用できます。
Statistics and Machine Learning Toolbox™ には、対数正規分布を処理する方法がいくつか用意されています。
確率分布を標本データに当てはめる (
fitdist) かパラメーター値を指定する (makedist) ことにより、確率分布オブジェクトLognormalDistributionを作成します。そして、オブジェクト関数を使用して、分布の評価や乱数の生成などを行います。分布フィッター アプリを使用して、対数正規分布を対話的に処理します。オブジェクトをアプリからエクスポートしてオブジェクト関数を使用できます。
分布パラメーターを指定して、分布特有の関数 (
logncdf、lognpdf、logninv、lognlike、lognstat、lognfit、lognrnd) を使用します。分布特有の関数では、複数の対数正規分布についてのパラメーターを受け入れることができます。分布名 (
'Lognormal') とパラメーターを指定して、汎用の分布関数 (cdf、icdf、pdf、random) を使用します。
パラメーター
対数正規分布は、次のパラメーターを使用します。
| パラメーター | 説明 | サポート |
|---|---|---|
mu (μ) | 対数値の平均 | |
sigma (σ) | 対数値の標準偏差 |
X がパラメーター µ および σ をもつ対数正規分布に従う場合、log(X) は平均 µ および標準偏差 σ をもつ正規分布に従います。
パラメーター推定
対数正規分布をデータに当てはめてパラメーター推定を求めるには、lognfit、fitdist または mle を使用します。
打ち切りがないデータの場合、
lognfitとfitdistは分布パラメーターの不偏推定量を、mleは最尤推定量を求めます。打ち切りがあるデータの場合、
lognfit、fitdistおよびmleは最尤推定量を求めます。
パラメーター推定を返す lognfit および mle と異なり、fitdist は当てはめた確率分布オブジェクト LognormalDistribution を返します。オブジェクト プロパティ mu および sigma にはパラメーター推定が格納されます。
記述統計
対数正規確率変数の平均 m と分散 v は、対数正規分布パラメーター µ および σ の関数です。
また、対数正規分布のパラメーター µ および σ は、平均 m と分散 v から計算できます。
確率密度関数
対数正規分布の確率密度関数 (pdf) は次のようになります。
たとえば、対数正規分布の確率密度関数の計算を参照してください。
累積分布関数
対数正規分布の累積分布関数 (cdf) は次のようになります。
たとえば、対数正規分布の累積分布関数の計算を参照してください。
例
対数正規分布の確率密度関数の計算
米国の 4 人家族の収入が mu = log(20,000) および sigma = 1 である対数正規分布に従っているものとします。収入の密度を計算してプロットします。
パラメーター値を指定して対数正規分布オブジェクトを作成します。
pd = makedist('Lognormal','mu',log(20000),'sigma',1)
pd =
LognormalDistribution
Lognormal distribution
mu = 9.90349
sigma = 1
pdf の値を計算します。
x = (10:1000:125010)'; y = pdf(pd,x);
確率密度関数をプロットします。
plot(x,y)
h = gca;
h.XTick = [0 30000 60000 90000 120000];
h.XTickLabel = {'0','$30,000','$60,000',...
'$90,000','$120,000'};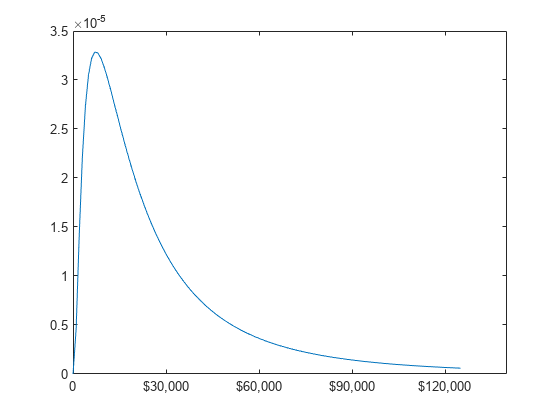
対数正規分布の累積分布関数の計算
平均 mu および標準偏差 sigma をもつ対数正規分布について、x 内の値で評価した cdf の値を計算します。
x = 0:0.2:10; mu = 0; sigma = 1; p = logncdf(x,mu,sigma);
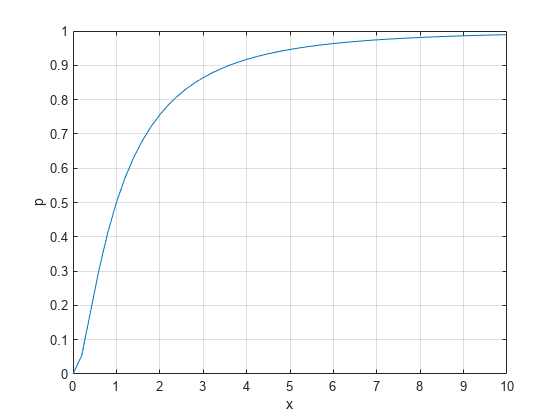
累積分布関数をプロットします。
plot(x,p) grid on xlabel('x') ylabel('p')
正規分布と対数正規分布の関係
X がパラメーター µ および σ をもつ対数正規分布に従う場合、log(X) は平均 µ および標準偏差 σ をもつ正規分布に従います。分布オブジェクトを使用して、正規分布と対数正規分布の関係を調べます。
パラメーター値を指定して対数正規分布オブジェクトを作成します。
pd = makedist('Lognormal','mu',5,'sigma',2)
pd =
LognormalDistribution
Lognormal distribution
mu = 5
sigma = 2
対数正規分布の平均値を計算します。
mean(pd)
ans = 1.0966e+03
対数正規分布の平均値は、mu パラメーターと等しくありません。対数値の平均は mu に等しくなります。乱数を生成して、この関係を確認します。
対数正規分布から乱数を生成し、その対数値を計算します。
rng('default'); % For reproducibility x = random(pd,10000,1); logx = log(x);
対数値の平均を計算します。
m = mean(logx)
m = 5.0033
x は対数正規分布に従うので、x の対数の平均は x の mu パラメーターに近くなっています。
正規分布近似を使用して、logx のヒストグラムを作成します。
histfit(logx)

このプロットは、x の対数値が正規分布に従うことを示しています。
histfit は、fitdist を使用して分布をデータに当てはめます。fitdist を使用して、当てはめに使用されたパラメーターを取得します。
pd_normal = fitdist(logx,'Normal')pd_normal =
NormalDistribution
Normal distribution
mu = 5.00332 [4.96445, 5.04219]
sigma = 1.98296 [1.95585, 2.01083]
推定された正規分布のパラメーターは、対数正規分布のパラメーター 5 および 2 に近くなっています。
対数正規分布とブール分布の pdf の比較
対数正規分布から生成された収入データを使用して、対数正規分布の pdf をブール分布の pdf と比較します。
収入データを生成します。
rng('default') % For reproducibility y = random('Lognormal',log(25000),0.65,[500,1]);
ブール分布を近似します。
pd = fitdist(y,'burr')pd =
BurrDistribution
Burr distribution
alpha = 26007.2 [21165.5, 31956.4]
c = 2.63743 [2.3053, 3.0174]
k = 1.09658 [0.775479, 1.55064]
収入データのブール分布と対数正規分布の両方の pdf を同じ Figure にプロットします。
p_burr = pdf(pd,sortrows(y)); p_lognormal = pdf('Lognormal',sortrows(y),log(25000),0.65); plot(sortrows(y),p_burr,'-',sortrows(y),p_lognormal,'-.') title('Burr and Lognormal pdfs Fit to Income Data') legend('Burr Distribution','Lognormal Distribution')

関連する分布
正規分布— 対数正規分布は、正規分布と密接に関連しています。X がパラメーター μ と σ をもつ対数正規分布の場合、log(x) は平均 μ と標準偏差 σ をもつ正規分布になります。正規分布と対数正規分布の関係を参照してください。
ブール型 XII 分布— ブール分布は柔軟な分布族であり、多岐にわたる分布形状を表現することができます。限定的なケースでは、ガンマ分布、対数正規分布、対数ロジスティック分布、つりがね型分布、(U 字型を除く) J 字型ベータ分布など、一般的に使用される分布になります。対数正規分布とブール分布の pdf の比較を参照してください。
参照
[1] Abramowitz, Milton, and Irene A. Stegun, eds. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. 9. Dover print.; [Nachdr. der Ausg. von 1972]. Dover Books on Mathematics. New York, NY: Dover Publ, 2013.
[2] Evans, M., N. Hastings, and B. Peacock. Statistical Distributions. 2nd ed., Hoboken, NJ: John Wiley & Sons, Inc., 1993.
[3] Lawless, J. F. Statistical Models and Methods for Lifetime Data. Hoboken, NJ: Wiley-Interscience, 1982.
[4] Marsaglia, G., and W. W. Tsang. “A Fast, Easily Implemented Method for Sampling from Decreasing or Symmetric Unimodal Density Functions.” SIAM Journal on Scientific and Statistical Computing. Vol. 5, Number 2, 1984, pp. 349–359.
[5] Meeker, W. Q., and L. A. Escobar. Statistical Methods for Reliability Data. Hoboken, NJ: John Wiley & Sons, Inc., 1998.
[6] Mood, A. M., F. A. Graybill, and D. C. Boes. Introduction to the Theory of Statistics. 3rd ed., New York: McGraw-Hill, 1974. pp. 540–541.
参考
LognormalDistribution | logncdf | lognpdf | logninv | lognlike | lognstat | lognfit | lognrnd