超幾何分布
定義
超幾何確率密度関数は、次の式で定義されます。
背景
超幾何分布は、有限の母集団から決まったサイズの標本を非復元抽出する場合の成功の総数をモデリングします。
この分布は、離散で、標本数または可能な成功数の内の大きい方よりも小さい、非負整数にのみ存在します。超幾何分布は、母集団が有限で、抽出が非復元である点についてのみ、二項分布と異なります。
超幾何分布は、直接的に物理的な解釈ができる 3 つのパラメーターをもちます。
M は、母集団のサイズです。
K は、母集団内で対象となる特徴をもつ個体の数です。
n は、取り出された標本の数です。
「非復元」抽出法とは、ある時点で特定の標本を選択すると、それより後のすべての選択で当該の母集団からこの標本が除外されることを意味します。
例
超幾何分布累積分布関数の計算とプロット
この例では、超幾何分布の累積分布関数の計算とプロット方法を示します。
1000 項目をもつグループから 20 件の標本を抽出する超幾何分布の累積分布関数を計算します。その際、グループには望ましい種類の項目が 50 件含まれているとします。
x = 0:10; y = hygecdf(x,1000,50,20);
累積分布関数をプロットします。
stairs(x,y)
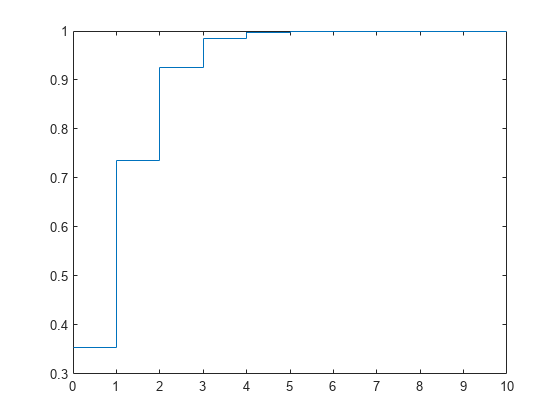
プロットの x 軸は、目的の種類の、抽出されたアイテム数を示しています。y 軸は、対応する累積分布関数の値を示しています。
参考
hygecdf | hygepdf | hygeinv | hygestat | hygernd | random