PiecewiseLinearDistribution
区分的線形確率分布オブジェクト
説明
PiecewiseLinearDistribution オブジェクトは、区分的線形確率分布のモデルの説明から構成されます。
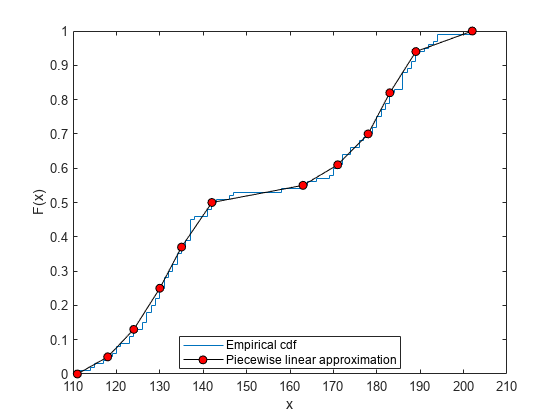
区分的線形分布は、累積分布関数 (cdf) の区分的線形表現を使って作成されるノンパラメトリック確率分布です。区分的線形分布に指定されるオプションで、累積分布関数の形式が指定されます。確率密度関数 (pdf) はステップ関数です。
区分線形分布は、次のパラメーターを使用します。
| パラメーター | 説明 |
|---|---|
x | 累積分布関数が傾きを変更する x 値のベクトル |
Fx | x の各値に対応する累積分布関数のベクトル |
作成
makedist を使用してパラメーター値を指定したオブジェクトにより、PiecewiseLinearDistribution 確率分布を作成します。
プロパティ
オブジェクト関数
例
既定のパラメーター値を使用して区分的線形分布オブジェクトを作成します。
pd = makedist('PiecewiseLinear')pd = PiecewiseLinearDistribution F(0) = 0 F(1) = 1
データの経験累積分布関数 (cdf) を計算し、この経験累積分布関数の近似を使用して区分的線形分布オブジェクトを作成します。
標本データを読み込みます。ヒストグラムを使用して患者の体重データを可視化します。
load patients histogram(Weight(strcmp(Gender,'Female'))) hold on histogram(Weight(strcmp(Gender,'Male'))) legend('Female','Male')
ヒストグラムは、データに女性の患者と男性の患者に 1 つずつ 2 つの最頻値があることを示しています。
データの経験累積分布関数を計算します。
[f,x] = ecdf(Weight);
5 点ごとに値を 1 つ採用し、経験累積分布関数への区分的線形近似を構成します。
f = f(1:5:end); x = x(1:5:end);
経験累積分布関数と近似をプロットします。
figure ecdf(Weight) hold on plot(x,f,'ko-','MarkerFace','r') legend('Empirical cdf','Piecewise linear approximation', ... 'Location','best')
経験累積分布関数の区分的近似を使用して、区分的線形確率分布オブジェクトを作成します。
pd = makedist('PiecewiseLinear','x',x,'Fx',f)
pd = PiecewiseLinearDistribution F(111) = 0 F(118) = 0.05 F(124) = 0.13 F(130) = 0.25 F(135) = 0.37 F(142) = 0.5 F(163) = 0.55 F(171) = 0.61 F(178) = 0.7 F(183) = 0.82 F(189) = 0.94 F(202) = 1
分布から 100 個の乱数を生成します。
rng('default') % For reproducibility rw = random(pd,[100,1]);
乱数をプロットして、分布を元のデータと視覚的に比較します。
figure histogram(Weight) hold on histogram(rw) legend('Original data','Generated data')
区分的線形分布から生成された乱数は、元のデータと同じ二峰性分布をもちます。
バージョン履歴
R2013a で導入
