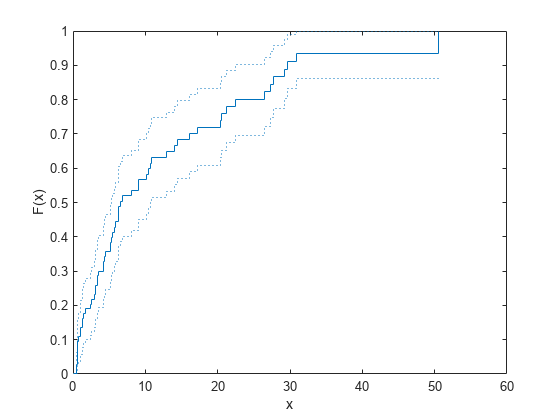
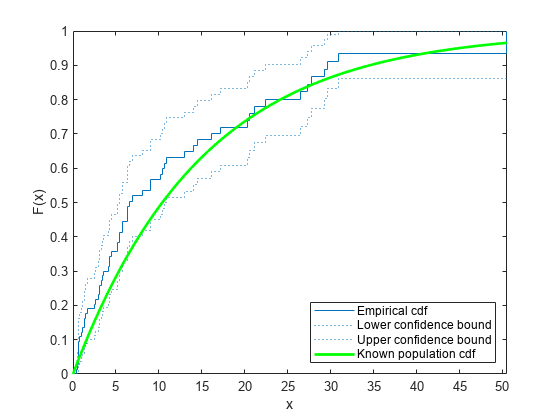
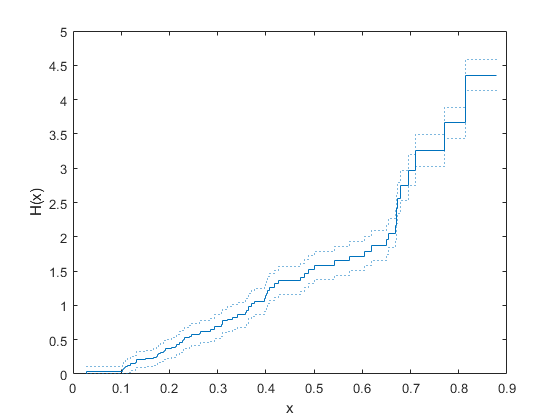
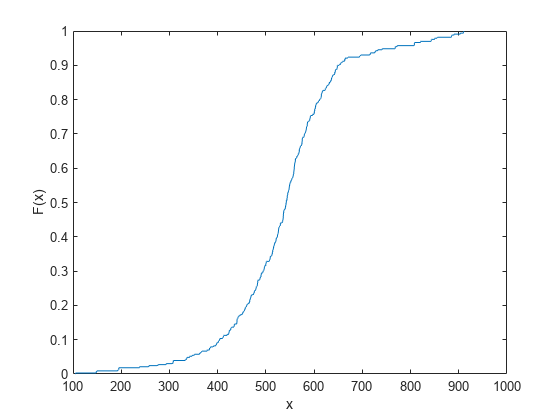
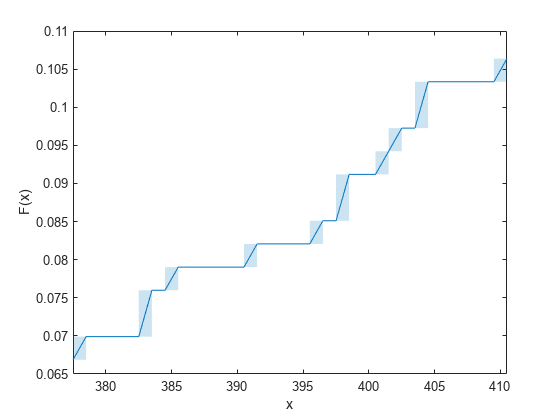
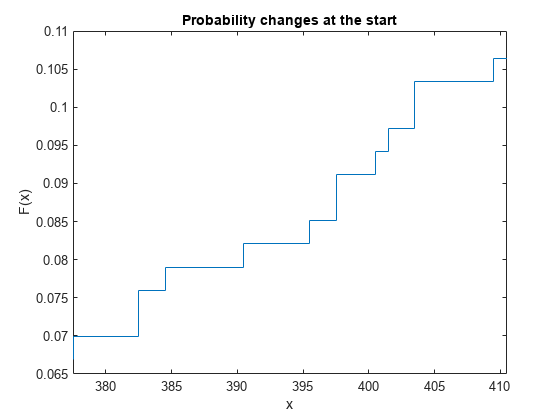
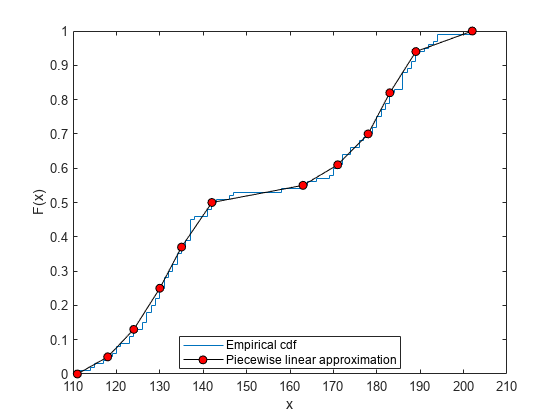
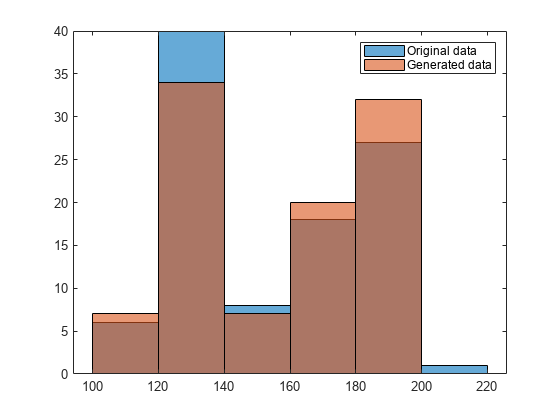
ecdf

経験的累積分布関数

構文

[f,x] = ecdf(y)

[f,x] = ecdf(y,Name,Value)

[f,x,flo,fup] = ecdf(___)

ecdf(___)

ecdf(ax,___)

説明

[f,x] = ecdf(y) は、y のデータを使用して、x の点で評価される、経験的累積分布関数 f を返します。

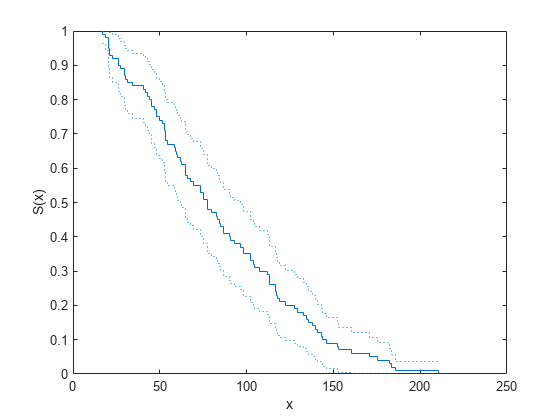
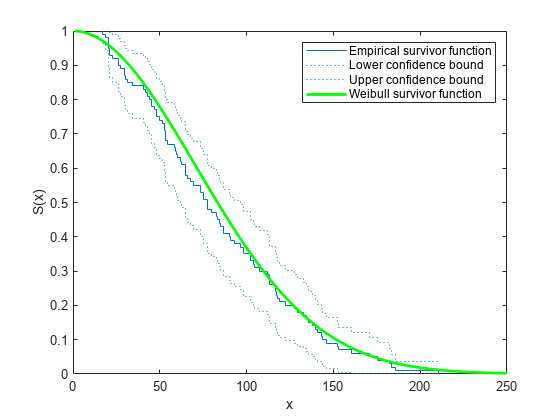
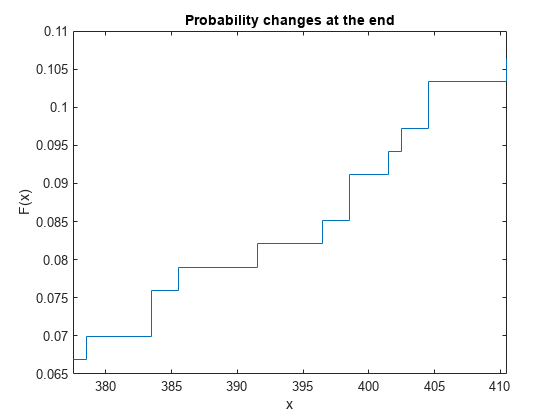
[f,x] = ecdf(y,Name,Value) では、1 つ以上の名前と値の引数を使用して追加オプションを指定します。たとえば、'Function','survivor' は、f の関数のタイプを生存時間関数として指定します。

[f,x,flo,fup] = ecdf(___) は、前の構文におけるいずれかの入力引数の組み合わせを使用して、評価された関数の値に対する信頼限界の下限および上限も返します。この構文は、区間打ち切りデータには有効ではありません。

ecdf(___) は、評価した関数の階段状グラフを生成します。この関数は、影付きの矩形を使用して、区間打ち切りデータの区間推定を可視化します。完全に観測されたデータ、左側打ち切りデータ、右側打ち切りデータ、および二重打ち切りデータの信頼限界をグラフに含めるために、'Bounds','on' を指定できます。

ecdf(ax,___) は、現在の座標軸 (gca) ではなく、ax によって指定された座標軸にプロットします。

例

経験的 cdf の計算

シミュレーションを実行した生存データの経験的累積分布関数 (cdf) のカプラン・マイヤー推定値を計算します。

パラメーター 3 と 1 を使用してワイブル分布から生存データを生成します。

rng('default')  % For reproducibility
failuretime = random('wbl',3,1,15,1);

生存データの経験的累積分布関数のカプラン・マイヤー推定値を計算します。

[f,x] = ecdf(failuretime);
[f,x]

ans = 16×2

         0    0.0895
    0.0667    0.0895
    0.1333    0.1072
    0.2000    0.1303
    0.2667    0.1313
    0.3333    0.2718
    0.4000    0.2968
    0.4667    0.6147
    0.5333    0.6684
    0.6000    1.3749
      ⋮

推定された経験的 cdf をプロットします。

ecdf(failuretime)

経験的 cdf と既知の cdf との比較

右側打ち切りの生存データを生成し、経験的累積分布関数 (CDF) と既知の累積分布関数を比較します。

平均故障時間 15 をもつ指数分布から故障時間を生成します。

rng('default')  % For reproducibility
y = exprnd(15,75,1);

平均故障時間 30 をもつ指数分布から脱落時間を生成します。

d = exprnd(30,75,1);

観測故障時間を生成します。つまり、生成された故障時間と脱落時間の最小値です。

t = min(y,d);

脱落時間よりも大きい生成された故障時間を含む logical 配列を作成します。この条件が真となるデータが打ち切られます。

censored = (y>d);

経験的累積分布関数と信頼限界を計算します。

[f,x,flo,fup] = ecdf(t,'Censoring',censored);

経験的累積分布関数と信頼限界をプロットします。

ecdf(t,'Censoring',censored,'Bounds','on')
hold on

既知の母集団の累積分布関数のプロットを重ね合わせます。

xx = 0:.1:max(t);
yy = 1-exp(-xx/15);
plot(xx,yy,'g-','LineWidth',2)
axis([0 max(t) 0 1])
legend('Empirical cdf','Lower confidence bound', ...
    'Upper confidence bound','Known population cdf', ...
    'Location','southeast')
hold off

信頼限界がある経験的生存時間関数のプロット

生存データを生成し、99% の信頼限界をもつ経験的生存時間関数をプロットします。

パラメーター 100 と 2 を使用してワイブル分布から寿命データを生成します。

rng('default')  % For reproducibility
R = wblrnd(100,2,100,1);

99% の信頼限界をもつデータの経験的生存時間関数をプロットします。

ecdf(R,'Function','survivor','Alpha',0.01,'Bounds','on')
hold on

ワイブル生存時間関数のプロットを重ね合わせます。

x = 1:1:250;
wblsurv = 1-cdf('weibull',x,100,2);
plot(x,wblsurv,'g-','LineWidth',2)
legend('Empirical survivor function','Lower confidence bound', ...
    'Upper confidence bound','Weibull survivor function', ...
    'Location','northeast')

実際の分布に基づくワイブル生存時間関数は、信頼限界内に入っています。

二重打ち切りデータの経験的累積ハザード関数

シミュレートされた二重打ち切り生存データの累積ハザード関数を計算およびプロットします。

バーンバウム・サンダース分布から故障時間を生成します。

rng('default')  % For reproducibility
failuretime = random('BirnbaumSaunders',0.3,1,[100,1]);

分析は時間 0.1 から開始し、時間 0.9 で終了すると仮定します。この仮定は、0.1 より小さい故障時間は左側打ち切りされ、0.9 より大きい故障時間は右側打ち切りされることを意味します。

各要素が failuretime の対応する観測の打ち切りステータスを示すベクトルを作成します。–1、1、および 0 を使用して、それぞれ左側打ち切り観測値、右側打ち切り観測値、完全に観測された観測値を示します。

L = 0.1;
U = 0.9;
left_censored = (failuretime<L);
right_censored = (failuretime>U);
c = right_censored - left_censored;

95% の信頼限界をもつデータの経験的累積ハザード関数をプロットします。

ecdf(failuretime,'Function','cumulative hazard', ...
    'Censoring',c,'Bounds','on')

区間打ち切りデータの経験的累積分布関数

区間打ち切りデータの経験的累積分布関数を計算してプロットします。

cities データ セットを読み込みます。このデータには、アメリカ合衆国の 329 の都市について、生活の質を表す 9 つの異なる指標 (気候、住宅、健康、犯罪、交通、教育、芸術、レクリエーション、経済) の評価点が含まれています。どの指標でも、評価点が高いほど優れています。

load cities

最初の指標 (気候) を標本データに選択します。

Y = ratings(:,1);

Y の指標は、最も近い整数に丸められた値であると仮定します。すると、Y の値を区間打ち切り観測値として扱えます。Y の観測値 y は、実際の評価点が y–0.5 と y+0.5 の間にあることを示しています。

各行が Y にあるそれぞれの整数を囲む区間を表している行列を作成します。

intervalY = [Y-0.5, Y+0.5];

経験的累積分布関数値を計算します。

[f,x] = ecdf(intervalY);

経験的累積分布関数値をプロットします。

figure
ecdf(intervalY)

より小さな領域にズーム インして、区間推定を確認します。

idx_roi = 21:30;
xlim([x(idx_roi(1),1) x(idx_roi(end),2)])

対応する x と f の値を表示します。

table(idx_roi',x(idx_roi,:),f(idx_roi,:), ...
    'VariableNames',{'Index','x','Empirical cdf F(x)'})

ans=10×3 table
    Index          x           Empirical cdf F(x)
    _____    ______________    __________________

     21      377.5    378.5         0.069909     
     22      382.5    383.5         0.075988     
     23      384.5    385.5         0.079027     
     24      390.5    391.5         0.082067     
     25      395.5    396.5         0.085106     
     26      397.5    398.5         0.091185     
     27      400.5    401.5         0.094225     
     28      401.5    402.5         0.097264     
     29      403.5    404.5          0.10334     
     30      409.5    410.5          0.10638     

影付きの矩形は、対応する区間内で経験的累積分布関数値 F(x) が変化していることを示します。たとえば、ズームしたプロットで左から 2 番目の影付きの矩形は、区間 (382.5,383.5] に対応します。F(382.5) は 0.075988、F(383.5) は 0.079027 で、0.075988 から 0.079027 への変化が区間 (382.5,383.5] で発生しています。変化の厳密なタイミングは不確定です。

区間推定はさまざまな方法でプロットできます。確率の変化が各区間の最初で生じていると仮定した場合、x の最初の列を使用して F(x) の値をプロットできます。

figure
stairs(x(:,1),f)
title('Probability changes at the start')
xlabel('x')
ylabel('F(x)')
xlim([x(idx_roi(1),1) x(idx_roi(end),2)])

もしくは、確率の変化が各区間の最後に生じていると仮定した場合、x の 2 番目の列を使用して F(x) の値をプロットできます。

figure
stairs(x(:,2),f)
title('Probability changes at the end')
xlabel('x')
ylabel('F(x)')
xlim([x(idx_roi(1),1) x(idx_roi(end),2)])

前の 2 つのプロットを組み合わせて、区間を可視化します。

figure
stairs(x(:,1),f)
hold on
stairs(x(:,2),f)
title('Probability changes in the interval')
xlabel('x')
ylabel('F(x)')
xlim([x(idx_roi(1),1) x(idx_roi(end),2)])
hold off

経験的累積分布関数からの区分的線形分布オブジェクトの作成

データの経験的累積分布関数 (cdf) を計算し、この経験的累積分布関数の近似を使用して区分的線形分布オブジェクトを作成します。

標本データを読み込みます。ヒストグラムを使用して患者の体重データを可視化します。

load patients
histogram(Weight(strcmp(Gender,'Female')))
hold on
histogram(Weight(strcmp(Gender,'Male')))
legend('Female','Male')

ヒストグラムは、データに女性の患者と男性の患者に 1 つずつ 2 つの最頻値があることを示しています。

データの経験的累積分布関数を計算します。

[f,x] = ecdf(Weight);

5 点ごとに値を 1 つ採用し、経験累積分布関数への区分的線形近似を構成します。

f = f(1:5:end);
x = x(1:5:end);

経験的累積分布関数と近似をプロットします。

figure
ecdf(Weight)
hold on
plot(x,f,'ko-','MarkerFace','r') 
legend('Empirical cdf','Piecewise linear approximation', ...
    'Location','best')

経験累積分布関数の区分的近似を使用して、区分的線形確率分布オブジェクトを作成します。

pd = makedist('PiecewiseLinear','x',x,'Fx',f)

pd = 
  PiecewiseLinearDistribution

F(111) = 0
F(118) = 0.05
F(124) = 0.13
F(130) = 0.25
F(135) = 0.37
F(142) = 0.5
F(163) = 0.55
F(171) = 0.61
F(178) = 0.7
F(183) = 0.82
F(189) = 0.94
F(202) = 1

分布から 100 個の乱数を生成します。

rng('default') % For reproducibility
rw = random(pd,[100,1]);

乱数をプロットして、分布を元のデータと視覚的に比較します。

figure
histogram(Weight)
hold on
histogram(rw)
legend('Original data','Generated data')

区分的線形分布から生成された乱数は、元のデータと同じ二峰性分布をもちます。

入力引数

y — 標本データおよび打ち切り情報

ベクトル | 2 列の行列

標本データおよび打ち切り情報。標本データのベクトルとして、または標本データおよび打ち切り情報からなる 2 列の行列として指定します。

引数 y または名前と値の引数 Censoring のいずれかを使用して、標本データの打ち切り情報を指定できます。y が 2 列の行列の場合、ecdf は引数 Censoring の値を無視します。

y の観測値の打ち切りタイプに応じて、y をベクトルまたは 2 列の行列として指定します。

• 完全に観測されたデータ — y を標本データのベクトルとして指定します。

• 完全に観測された観測値、左側打ち切り観測値、または右側打ち切り観測値を含むデータ — 標本データのベクトルとして y を指定し、各観測値の打ち切り情報を含むベクトルとして名前と値の引数 Censoring を指定します。Censoring ベクトルには 0、-1、および 1 を含められます。それぞれ完全に観測された観測値、左側打ち切り観測値、右側打ち切り観測値を参照します。

• 区間打ち切り観測値を含むデータ — y を、標本データおよび打ち切り情報からなる 2 列の行列として指定します。y の各行は、各観測値に対する可能な生存時間および故障時間の範囲を指定します。以下の値のいずれかにできます。

  • [t,t] — t で完全に観測

  • [–Inf,t] — t で左側打ち切り

  • [t,Inf] — t で右側打ち切り

  • [t1,t2] — [t1,t2] 間で区間打ち切り (t1 < t2)

ecdf は、y 内の NaN 値を無視します。また、打ち切りベクトル (Censoring) または頻度ベクトル (Frequency) に NaN 値が含まれている場合、ecdf は y 内の対応する行を無視します。

データ型: single | double

ax — ターゲットの座標軸

Axes オブジェクト

ecdf がプロットする図のターゲットの座標軸。Axes オブジェクトとして指定します。

たとえば、h が図のターゲット Axes オブジェクトである場合、ecdf はこの図に次の例のようにプロットできます。

例: ecdf(h,x)

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで Name は引数名、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: 'Censoring',c,'Function','cumulative hazard','Alpha',0.025,'Bounds','on' は、ベクトル c で指定された打ち切りデータを考慮して、ecdf が累積ハザード関数および 97.5% の信頼限界を返すように指示します。

Function — 返される関数のタイプ

'cdf' (既定値) | 'survivor' | 'cumulative hazard'

ecdf が返す関数のタイプ。次のいずれかの値を指定します。

値	説明
'cdf' (既定の設定)	累積分布関数 (cdf)
'survivor'	生存時間関数
'cumulative hazard'	累積ハザード関数

例: 'Function','cumulative hazard'

Censoring — 打ち切りデータのインジケーター

0 のベクトル (既定値) | 0、–1、および 1 からなるベクトル

打ち切りデータのインジケーター。0、–1 および 1 からなるベクトルとして指定します。それぞれ完全に観測された観測値、左側打ち切り観測値、右側打ち切り観測値を示します。Censoring 値の各要素は、y の対応する観測の打ち切りステータスを示します。Censoring 値は、y と同じサイズでなければなりません。既定の設定は 0 のベクトルで、すべての観測値が完全に観測されていることを示します。

この引数を使用しても、区間打ち切り観測値は指定できません。標本データに区間打ち切り観測値が含まれる場合、2 列の行列を使用して y を指定します。ecdf は、y が 2 列の行列の場合に Censoring 値を無視します。

ecdf は、打ち切りベクトルにある任意の NaN 値を無視します。さらに、y または頻度ベクトル (Frequency) に NaN 値が含まれている場合、ecdf は打ち切りベクトル内の対応する値を無視します。

例: 'Censoring',censored。ここで、censored は打ち切り情報を含むベクトルです。

データ型: logical | single | double

Frequency — 観測の頻度

1 から成るベクトル (既定値) | 非負のスカラーのベクトル

観測の頻度。y と同じ行数をもつ非負の整数カウントのベクトルとして指定します。Frequency 値の j 番目の要素は、y の j 番目の行が観測された回数を示します。既定値は 1 のベクトルで、y の行あたり 1 回の観測を意味します。

ecdf は、この頻度ベクトルの NaN 値をすべて無視します。さらに、y または打ち切りベクトル (Censoring) に NaN 値が含まれている場合、ecdf は頻度ベクトル内の対応する値を無視します。

例: 'Frequency',freq。ここで、freq は観測頻度を含むベクトルです。

データ型: single | double

IterationLimit — 最大反復回数

1e7 (既定値) | 正の整数

最大反復回数。正の整数を指定します。この引数は、二重打ち切りデータおよび区間打ち切りデータのみで有効です。

例: 'IterationLimit',1e5

データ型: single | double

Tolerance — 関数値の終了許容誤差

1e-7 (既定値) | 正のスカラー

関数の値 f の終了許容誤差。正のスカラーを指定します。この引数は、二重打ち切りデータおよび区間打ち切りデータのみで有効です。

例: 'Tolerance',1e-5

データ型: single | double

ICMFrequency — ICM ステップの頻度

10 (既定値) | 正の整数

反復凸劣関数 (ICM) ステップの頻度。正の整数を指定します。この引数は区間打ち切りデータに対してのみ有効です。

ecdf は、期待値最大化反復凸劣関数 (EMICM) アルゴリズム [5] を使用して、区間打ち切りデータの出力 f を計算します。EMICM アルゴリズムは各反復時に EM アルゴリズムまたは ICM アルゴリズムを使用します。ecdf は、指定した反復回数ごとに ICM ステップを実行します。たとえば既定の設定では、ecdf は EM ステップを 9 回繰り返し、ICM ステップを 1 回実行した後、EM ステップに戻ります。

例: 'ICMFrequency',1

データ型: single | double

Alpha — 有意水準

0.05 (既定値) | 範囲 (0,1) のスカラー

評価した関数の信頼区間の有意水準。範囲 (0,1) のスカラーを指定します。既定値は 0.05 で、95% の信頼度を意味します。値 alpha を指定すると、信頼水準は 100(1 – Alpha)% になります。

この引数は、区間打ち切りデータには有効ではありません。

例: 'Alpha',0.01 は信頼水準を 99% として指定します。

データ型: single | double

Bounds — プロットに信頼限界を含めるかどうかのインジケーター

'off' (既定値) | 'on'

プロットに信頼限界を含めるかどうかのインジケーター。次のいずれかの値を指定します。

値	説明
'off' (既定の設定)	信頼限界を省略します。
'on'	信頼限界を含めます。

この引数は、区間打ち切りデータには有効ではありません。

メモ

この引数はプロットに対してのみ有効です。

例: 'Bounds','on'

出力引数

f — 関数値

列ベクトル

x 内の点または区間で評価される関数値。列ベクトルとして返されます。

• 点の推定は、x(i) での関数の値が f(i) であることを示します。

• 区間の推定は、区間 (x(i,1),x(i,2)] 内で関数の値が f(i–1) から f(i) に変化することを示します。変化の厳密なタイミングは不確定です。例については、区間打ち切りデータの経験的累積分布関数を参照してください。

f の関数タイプは、名前と値の引数 Function で指定されるように、cdf (既定)、生存時間関数、または累積ハザード関数にできます。

x — 評価点または評価区間

列ベクトル | 2 列の行列

評価点または評価区間。それぞれ列ベクトルまたは 2 列の行列として指定します。

• ecdf は、完全に観測されたデータ、左側打ち切りデータ、右側打ち切りデータ、および二重打ち切りデータの列ベクトルを返します。

  • 完全に観測されたデータ、左側打ち切りデータ、右側打ち切りデータの場合、ecdf は、y から打ち切り観測の値を削除し、残りの値を並べ替え、ソートした値にある重複する値を削除して、結果を出力 x に保存します。

  • 二重打ち切りデータの場合、ecdf は、y のどの値がイベント時間に対応するかを決定し、値を並べ替え、並べ替えた値にある重複する値を削除して、結果を出力 x に保存します。

  出力 x には、最初の 2 つの値として y の最小値が格納されます。この 2 つの値は、関数 stairs を使用して ecdf の出力をプロットするために役立ちます。

• ecdf は区間打ち切りデータに対して 2 列の行列を返します。ecdf はターンブル区間と呼ばれる区間で関数値 f を評価します。詳細については、アルゴリズムを参照してください。

flo — 信頼限界の下限

列ベクトル

評価された関数の信頼限界の下限。列ベクトルとして返されます。ecdf は各観測の限界を計算します。flo はこの曲線の同期区間ではありません。

この引数は、区間打ち切りデータには有効ではありません。

fup — 信頼限界の上限

列ベクトル

評価された関数の信頼限界の上限。列ベクトルとして返されます。ecdf は各観測の限界を計算します。fup はこの曲線の同期区間ではありません。

この引数は、区間打ち切りデータには有効ではありません。

詳細

打ち切りのタイプ

ecdf は、左側打ち切り観測値、右側打ち切り観測値、および区間打ち切り観測値をサポートします。

• 時間 t での左側打ち切り観測 — 時間 t より前に発生したイベント。厳密なイベント時間は不明です。

• 時間 t での右側打ち切り観測 — 時間 t より後に発生したイベント。厳密なイベント時間は不明です。

• 区間 [t1,t2] 内の区間打ち切り観測 — 時間 t1 より後かつ時間 t2 より前に発生したイベント。厳密なイベント時間は不明です。

二重打ち切りデータには、左側打ち切り観測値および右側打ち切り観測値の両方が含まれます。

生存時間関数

生存時間関数とは、時間の関数としての生存の確率です。これは生存時間関数とも呼ばれます。

生存時間関数は、個体の生存時間が特定の値を超える確率を示します。累積分布関数 F(t) は、生存時間が特定の時点 t 以下である確率のため、連続分布の生存時間関数 S(t) は、累積分布関数の補数となります。S(t) = 1 – F(t)。

累積ハザード関数

ハザード関数 h(t) は、個体が一定時間まで生存した事実に基づいて条件付けられた個体の瞬間故障率です。累積ハザード関数 H(t) は、時間 t までの累積ハザードです。

$$h(t)=\underset{\Delta t\to 0}{\lim }\frac{P\left(t\le T<t+\Delta t|T\ge t\right)}{\Delta t},$$

$$H(t)={\displaystyle {\int }_0^{t}h(u)du}.$$

ハザード関数は常に正の値を取ります。ただし、これらの値は確率を表すものではないため、1 を超える可能性があります。

関係 S(t) = exp(–H(t)) を使用して、生存時間関数 S(t) から累積ハザード関数の値を取得できます。

アルゴリズム

ecdf は、打ち切り情報に応じて異なるアルゴリズムを使用し、関数値 (f) および信頼限界 (flo および fup) を計算します。f の関数タイプは、名前と値の引数 Function で指定されるように、cdf (既定)、生存時間関数、または累積ハザード関数にできます。

打ち切りのタイプ	f のアルゴリズム	flo および fup のアルゴリズム
右側打ち切りデータ。完全に観測された観測値または右側打ち切り観測値を含む	cdf 値および生存時間関数値にカプラン・マイヤー推定器を使用します。 カプラン・マイヤー推定器 $$\widehat{S}(t)$$ は次の式で与えられます。 $$\widehat{S}\left(t\right)={\displaystyle \prod _{t_i<t}\frac{r_i-d_i}{r_i}},$$ ここで、ri は時間 ti においてリスクにある観測数、di は時間 ti における故障数です。詳細については、カプラン・マイヤー法を参照してください。 累積ハザード関数値にネルソン・アーラン推定器を使用します。 ネルソン・アーラン推定器は次の式で与えられます。 $$\widehat{H}\left(t\right)={\displaystyle \sum _{t_i<t}\frac{d_i}{r_i}}.$$	グリーンウッドの公式を使用します。この式はカプラン・マイヤー推定器の分散の近似です。 分散推定は次の式で与えられます。 $$V\left(\widehat{S}\left(t\right)\right)={\widehat{S}}^2\left(t\right){\displaystyle \sum _{t_i<t}\frac{d_i}{r_i\left(r_i-d_i\right)}}.$$
左側打ち切りデータ。完全に観測された観測値または左側打ち切り観測値を含む	カプラン・マイヤー推定器を使用します。	グリーンウッドの公式を使用します。
二重打ち切りデータ。右側打ち切り観測値および左側打ち切り観測値の両方を含む	ターンブルのアルゴリズム [3][4] を使用します。アルゴリズムに対して最大反復回数 (IterationLimit) および関数値の終了許容誤差 (Tolerance) を指定できます。	フィッシャー情報行列を使用します。
区間打ち切りデータ。区間打ち切り観測値を含む	期待値最大化反復凸劣関数 (EMICM) アルゴリズム [5] を使用します。EMICM アルゴリズムは各反復時に EM アルゴリズムまたは ICM アルゴリズムを使用します。名前と値の引数 ICMFrequency は、ICM アルゴリズムの頻度を決定します。ecdf は、指定した反復回数ごとに ICM ステップを実行します。既定の設定では、ecdf は EM ステップを 9 回繰り返し、ICM ステップを 1 回実行した後、EM ステップに戻ります。アルゴリズムに対して最大反復回数 (IterationLimit) および関数値の終了許容誤差 (Tolerance) を指定できます。 ecdf は、2 列の行列データ y からターンブル区間と呼ばれる互いに重複しない区間を構築し、ターンブル区間 (x) およびこの区間の推定値 (f) を返します。区間の左限は y の 1 番目の列から、区間の右限は y の 2 番目の列からです。完全に観測された観測値 (2 つが同じ値 [t t] となる行) の場合、関数が [t t] を [t–eps(t) t] に変換し、ターンブル区間を構築する前に非ゼロの長さの区間を作成します。	サポートなし

参照

[1] Cox, D. R., and D. Oakes. Analysis of Survival Data. London: Chapman & Hall, 1984.

[2] Lawless, J. F. Statistical Models and Methods for Lifetime Data. 2nd ed., Hoboken, NJ: John Wiley & Sons, Inc., 2003.

[3] Klein, John P., and Melvin L. Moeschberger. Survival Analysis: Techniques for Censored and Truncated Data. 2nd ed. Statistics for Biology and Health. New York: Springer, 2003.

[4] Turnbull, Bruce W. "Nonparametric Estimation of a Survivorship Function with Doubly Censored Data." Journal of the American Statistical Association 69, No. 345 (1974): 169–73.

[5] Anderson-Bergman, Clifford. "An Efficient Implementation of the EMICM Algorithm for the Interval Censored NPMLE." Journal of Computational and Graphical Statistics 26, no. 2 (April 3, 2017): 463–67.

[6] Ware, James H., and David L. Demets. "Reanalysis of Some Baboon Descent Data." Biometrics 32, no. 2 (June 1976): 459–63.

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意事項および制限事項:

• コード生成で非有限サポートを無効にし、y を使用した左側打ち切りまたは右側打ち切りのデータを 2 列の行列の形式で指定する場合は、–Inf と Inf の代わりに min(y(~isinf(y))) より小さい値と max(y(~isinf(y))) より大きい値をそれぞれ使用します。

• プロットはコード生成でサポートされません。

• 名前と値の引数に含まれる名前はコンパイル時の定数でなければなりません。

• 名前と値の引数 'Function' の値はコンパイル時の定数でなければなりません。たとえば、生成されたコードで名前と値の引数 'Function','survivor' を使用するには、{coder.Constant('Function'),coder.Constant('survivor')} を codegen の -args の値に含めます。

コード生成の詳細については、コード生成の紹介および一般的なコード生成のワークフローを参照してください。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

この関数は、GPU 配列を完全にサポートします。詳細は、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2006a より前に導入

参考

cdfplot | ecdfhist

トピック

• さまざまなグループのハザード関数と生存時間関数
• 2 つのグループの生存時間関数
• 生存時間分析とは
• カプラン・マイヤー法