カプラン・マイヤー法

Statistics and Machine Learning Toolbox™ の関数 ecdf は、カプラン・マイヤーのノンパラメトリック手法を使用して、経験的累積ハザード関数、生存時間関数および累積分布関数を生成します。生存時間関数のカプラン・マイヤー推定器は、"積極限推定器" とも呼ばれます。

カプラン・マイヤー法では、生命表にまとめられた生存データを使用します。生命表では、昇順の故障時間に従ってデータが順序付けられますが、ecdf を使用するために故障または生存時間を順番どおりに入力する必要はありません。

生命表は通常、以下で構成されています。

故障時間
1 回/期間に故障したアイテム数
1 回/期間に打ち切られたアイテム数
1 回/期間の開始時にリスクがあるアイテムの数

リスクのある数は、各期間の開始時の総生存数です。最初の期間の開始時にリスクのある数は、寿命研究の対象となるすべての個体です。残りの各期間の開始時におけるリスクのある数は、故障の回数と、前の期間の終わりに打ち切られた個体の数を加算した分だけ減少します。

次の生命表には、架空の生存データが示されています。最初の故障時間の開始時において、リスクのあるアイテムが 7 つあります。時間 4 では、3 つのアイテムが故障します。したがって、時間 7 の開始時において、リスクのあるアイテムは 4 つになります。時間 7 では 1 個のみ故障したため、時間 11 の開始時においてリスクのある数は 3 になります。時間 11 には 2 個故障したため、時間 12 の開始時においてリスクのある数は 1 になります。残りのアイテムは時間 12 に故障します。

故障時間 (t)	故障した回数	リスクのある数
4	3	7
7	1	4
11	2	3
12	1	1

次の説明に従って生命表を使用して、ハザード関数、累積ハザード関数、生存時間関数および累積分布関数を推定できます。

累積ハザード率 (故障率)

各期間のハザード率は、特定期間の故障の回数をその期間の開始時に生存している個体の数 (リスクのある数) で割って得られます。

故障時間 (t)	ハザード率 (h(t))	累積ハザード率
0	0	0
t₁	d₁/r₁	d₁/r₁
t₂	d₂/r₂	h(t₁) + d₂/r₂
...	...	...
t_n	d_n/r_n	h(t_{n – 1}) + d_n/r_n

生存確率

各期間の生存確率は、ハザード率の補数の積です。最初の期間の開始時における初期生存確率は 1 です。各期間のハザード率が h(t_i) である場合、生存確率は次のようになります。

時間 (t)	生存確率 (S(t))
0	1
t₁	1*(1 – h(t₁))
t₂	S(t₁)*(1 – h(t₂))
...	...
t_n	S(t_{n – 1})*(1 – h(t_n))

累積分布関数

累積分布関数 (cdf) と生存時間関数は相互の補数であるため、F(t) = 1 – S(t) を使用して生命表から累積分布関数を見つけることができます。

このページの最初の表にある、シミュレーションを実行済みのデータについて、次のように累積ハザード率、生存率および累積分布関数を計算できます。

t	故障した回数 (d)	リスクのある数 (r)	ハザード率	生存確率	累積分布関数
4	3	7	3/7	1 – 3/7 = 4/7 = 0.5714	0.4286
7	1	4	1/4	4/7*(1 – 1/4) = 3/7 = .4286	0.5714
11	2	3	2/3	3/7*(1 – 2/3) = 1/7 = 0.1429	0.8571
12	1	1	1/1	1/7*(1 – 1) = 0	1

この例で取り上げる率は離散故障時間に基づいているため、計算は必ずしも生存時間分析とはの導関数に基づく定義に従っていません。

ここでは、ecdf を使用してデータを入力し、これらの尺度を計算する方法を示します。データは必ずしも昇順にする必要はありません。故障時間は配列 y に保存されるとします。

y = [4 7 11 12];
freq = [3 1 2 1];
[f,x] = ecdf(y,'frequency',freq)

データを打ち切った場合、生命表は次のようになります。

時間 (t)	故障した回数 (d)	打ち切り	リスクのある数 (r)	ハザード率	生存確率	累積分布関数
4	2	1	7	2/7	1 – 2/7 = 0.7143	0.2857
7	1	0	4	1/4	0.7143*(1 – 1/4) = 0.5357	0.4643
11	1	1	3	1/3	0.5357*(1 – 1/3) = 0.3571	0.6429
12	1	0	1	1/1	0.3571*(1 – 1) = 0	1.0000

どの時間でも、リスクのある数の合計において打ち切られたアイテムも考慮され、ハザード率の式は故障した回数とリスクのある合計数に基づきます。各期間の開始時にリスクのある数を更新し、前の期間で故障した回数と打ち切られた数の合計が、その期間の開始時のリスクのある数から差し引かれます。

ecdf を使用している間は、バイナリ変数の配列を使用して打ち切り情報も入力しなければなりません。打ち切られたデータについては 1 を入力し、正確な故障時間については 0 を入力します。

y = [4 4 4 7 11 11 12];
cens = [0 1 0 0 1 0 0];
[f,x] = ecdf(y,'censoring',cens)

ecdf は、既定では累積分布関数の値を生成します。最適な名前と値のペア引数を使用して、生存時間関数またはハザード関数を指定する必要があります。また、結果を次のようにプロットすることもできます。

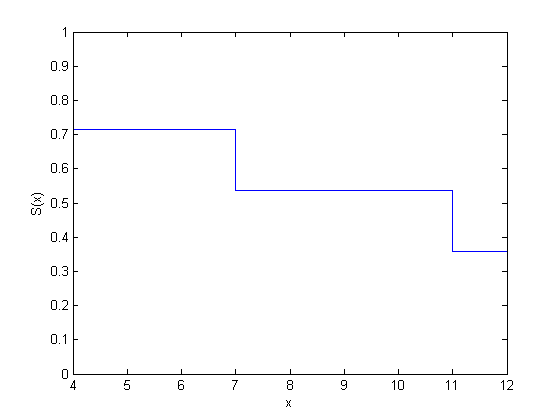
figure()
ecdf(y,'censoring',cens,'function','survivor');

Plot of survival probability versus x.

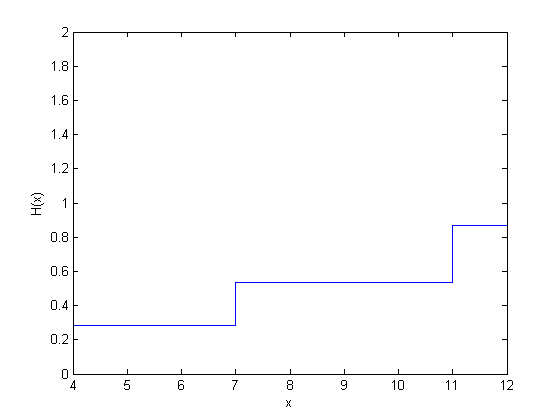
figure()
ecdf(y,'censoring',cens,'function','cumulative hazard');

Plot of cumulative hazard rate versus x.

参照

[1] Cox, D. R., and D. Oakes. Analysis of Survival Data. London: Chapman & Hall, 1984.

[2] Lawless, J. F. Statistical Models and Methods for Lifetime Data. Hoboken, NJ: Wiley-Interscience, 2002.

[3] Kleinbaum, D. G., and M. Klein. Survival Analysis. Statistics for Biology and Health. 2nd edition. Springer, 2005.

参考

ecdf | coxphfit | ksdensity

カプラン・マイヤー法

参照

参考

関連する例

詳細