paretotails
パレート分布の裾をもつ区分的分布
説明
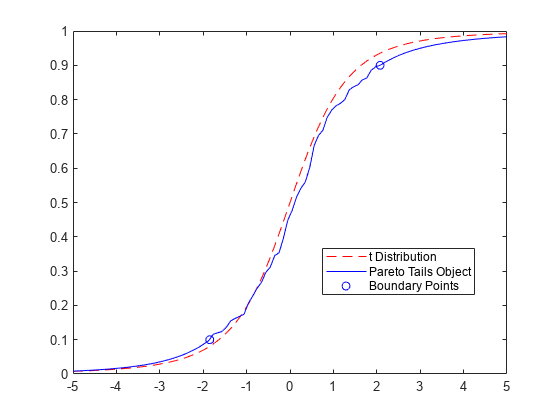
paretotails オブジェクトは、裾が一般化パレート分布 (GPD) になっている区分的分布です。
paretotails オブジェクトは、裾についての 1 つまたは 2 つの GPD と中央についての別の分布から構成されます。中央の分布タイプは、オブジェクトを作成するときに paretotails の引数 cdffun を使用することにより指定できます。有効な値は、'ecdf'、'kernel' および関数ハンドルです。
paretotails は、cdffun タイプの分布を観測値 (x) に当てはめ、下裾と上裾の累積確率 (それぞれ pl および pu) に対応する分位数を求めます。そして、paretotails は、2 つの GPD を観測値の下位 100*pl パーセントと観測値の上位 100*(1–pu) パーセントにそれぞれ当てはめます。2 つ以上の異なる観測値が x の裾に含まれていない場合、paretotails は対応する裾のセグメントを作成しません。
分布特性を調べるには、オブジェクト関数 boundary、segment、upperparams および lowerparams を使用します。lowerparams と upperparams は、裾の GPD のパラメーターを返します。boundary は、区分的分布のセグメント間の境界点を返します。segment は、入力値が含まれている区分的分布のセグメントを返します。nsegments は、オブジェクト内のセグメント数を返します。
分布を評価するには、オブジェクト関数 cdf、icdf、pdf および random を使用します。これらの関数は、コピュラや他のモンテカルロ シミュレーションに適しています。pdf は、裾における GPD の密度と中央における累積分布関数 (cdf) の傾きを返します。一般に、中央におけるこれらの確率密度関数 (pdf) の値は、元のデータの基となる密度の良好な推定ではありません。
作成
区分的分布オブジェクトの作成には paretotails を使用します。
説明
入力引数
プロパティ
オブジェクト関数
boundary | 区分的分布境界 |
cdf | 累積分布関数 |
icdf | 逆累積分布関数 |
lowerparams | 下裾のパレート分布のパラメーター |
nsegments | 区分的分布のセグメント数 |
pdf | 確率密度関数 |
random | 乱数 |
segment | 入力値が含まれている区分的分布のセグメント |
upperparams | 上裾のパレート分布のパラメーター |
例
標本データ セットを生成し、裾がパレート分布になっている区分的分布をデータに当てはめます。既定の設定で paretotails を使用して、中央について経験分布を指定します。
自由度が 3 の t 分布から、100 個の乱数が含まれている標本データ セットを生成します。
rng('default'); % For reproducibility t = trnd(3,100,1);
区分的分布を t に当てはめることにより paretotails オブジェクトを作成します。当てはめたオブジェクトがデータ セットの中程の 80% については経験分布、データ セットの下位および上位 10% については GPD から構成されるように、下裾と上裾の累積確率を使用して裾の境界を指定します。
pd = paretotails(t,0.1,0.9)
pd =
Piecewise distribution with 3 segments
-Inf < x < -1.84875 (0 < p < 0.1): lower tail, GPD(0.183032,1.00347)
-1.84875 < x < 2.07662 (0.1 < p < 0.9): interpolated empirical cdf
2.07662 < x < Inf (0.9 < p < 1): upper tail, GPD(0.333239,1.19705)
オブジェクト表示の各行には、GPD のパラメーター (形状パラメーターとスケール パラメーター) や、分位数および累積確率による境界の値など、各セグメントの要約が表示されます。これらの値を返すには、オブジェクト関数 boundary、lowerparams および upperparams を使用します。
関数 nsegments を使用すると、セグメント数を取得できます。関数 segment を使用すると、入力値が含まれているセグメントを取得できます。
分布関数 cdf、icdf、pdf および random を使用すると、分布の評価と無作為標本の生成を行うことができます。
t 分布の cdf と paretotails オブジェクトの cdf を同じ Figure にプロットします。
x = linspace(-5,5); plot(x,tcdf(x,3),'r--') hold on plot(x,cdf(pd,x),'b-')
boundary を使用して paretotails オブジェクトのセグメント間の境界の点を求め、これらの点を Figure 上でマークします。
[p,q] = boundary(pd); plot(q,p,'bo') legend('t Distribution','Pareto Tails Object','Boundary Points','Location','best') hold off
標本データ セットを生成し、裾がパレート分布になっている区分的分布をデータに当てはめます。paretotails と関数ハンドルを使用して、中央のセグメントを当てはめます。
20% の外れ値が含まれている標本データ セットを生成します。
rng('default'); % For reproducibility left_tail = -exprnd(1,100,1); right_tail = exprnd(5,100,1); center = randn(800,1); x = [left_tail;center;right_tail];
ksdensity を使用して関数ハンドルを定義し、既定値ではない帯域幅を指定します。
myfun1 = @(x)ksdensity(x,'Bandwidth',.1,'Function','cdf');
カーネル平滑化推定器を使用して区分的分布を x に当てはめることにより、paretotails オブジェクトを作成します。当てはめたオブジェクトがデータ セットの中央 80% についてはカーネル推定器、データ セットの下位および上位 10% については GPD から構成されるように、下裾と上裾の累積確率を使用して裾の境界を指定します。
pd1 = paretotails(x,0.1,0.9,myfun1)
pd1 =
Piecewise distribution with 3 segments
-Inf < x < -1.35204 (0 < p < 0.1): lower tail, GPD(0.0104112,0.54947)
-1.35204 < x < 1.80824 (0.1 < p < 0.9): function: @(x)ksdensity(x,'Bandwidth',.1,'Function','cdf')
1.80824 < x < Inf (0.9 < p < 1): upper tail, GPD(0.227542,3.10586)
中央のセグメントについてパラメトリック分布を使用することもできます。正規分布をデータに当てはめて cdf の値を返す関数を定義し、paretotails オブジェクトの作成時にその関数ハンドルを渡します。
pd2 = paretotails(x,0.1,0.9,@myfun2)
pd2 =
Piecewise distribution with 3 segments
-Inf < x < -2.70875 (0 < p < 0.1): lower tail, GPD(-0.358104,0.831855)
-2.70875 < x < 3.52195 (0.1 < p < 0.9): function: myfun2
3.52195 < x < Inf (0.9 < p < 1): upper tail, GPD(-0.0661815,5.04694)
function [p,xi] = myfun2(x) pd = fitdist(x,'Normal'); xi = linspace(min(x),max(x),length(x)*2); p = cdf(pd,xi); end
バージョン履歴
R2007a で導入
