パレート分布の裾を使用したノンパラメトリック分布の近似
この例では、パレート分布の裾を使用してノンパラメトリック確率分布を標本データに当てはめ、裾の分布を滑らかにする方法を示します。
手順 1. 標本データを生成します。
標準正規分布から想定される以上の外れ値を含む標本データを生成します。
rng('default') % For reproducibility left_tail = -exprnd(1,10,1); right_tail = exprnd(5,10,1); center = randn(80,1); data = [left_tail;center;right_tail];
データには、標準正規分布から 80% の値、平均が 5 の指数分布から 10% の値、平均が -1 の指数分布から 10% の値が含まれます。標準正規分布と比較すると、特に上裾の指数値は外れ値になる可能性が高くなります。
手順 2. 確率分布をデータに当てはめる。
正規分布と t 位置-スケール分布をデータに当てはめ、プロットして視覚的に比較します。
probplot(data); hold on p = fitdist(data,'tlocationscale'); h = plot(gca,p,'PlotType',"probability"); set(h,'color','r','linestyle','-'); title('Probability Plot') legend('Normal','Data','t location-scale','Location','SE') hold off
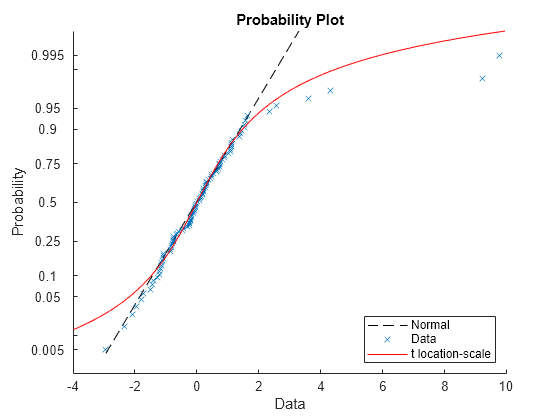
両方の分布は中央でよく適合しているように見えますが、正規分布と t 位置-スケール分布のどちらも裾で適切には適合していません。
手順 3. 経験分布を生成する。
より優れた近似を得るためには、ecdf を使用して、標本データに基づいた経験累積分布関数を生成します。
figure ecdf(data)
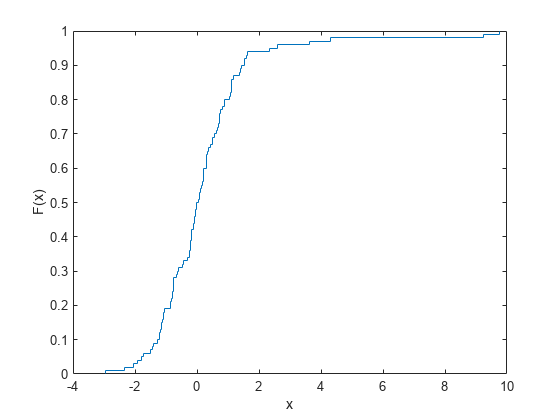
経験分布は完全に近似しますが、外れ値によって裾の部分がかなり離散的になります。この分布から逆関数法を使用して作成される無作為標本には、4.33 と 9.25 付近の値などが含まれることもありますが、その中間値は含まれません。
手順 4. パレート分布の裾を使用して分布を近似させる。
paretotails を使用して、データの中央 80% に経験累積分布関数を生成し、上下の 10% に生成されたパレート分布を近似します。
pfit = paretotails(data,0.1,0.9)
pfit =
Piecewise distribution with 3 segments
-Inf < x < -1.24623 (0 < p < 0.1): lower tail, GPD(-0.334156,0.798745)
-1.24623 < x < 1.48551 (0.1 < p < 0.9): interpolated empirical cdf
1.48551 < x < Inf (0.9 < p < 1): upper tail, GPD(1.23681,0.581868)
より優れた近似を得るため、paretotails は、標本の中央の ecdf またはカーネル分布と裾の滑らかな一般化パレート分布 (GPD) をつなぎ合わせた分布を近似します。paretotailsを使用して paretotails 確率分布オブジェクトを作成します。paretotails オブジェクトのオブジェクト関数を使用すると、当てはめに関する情報にアクセスし、オブジェクトに対する計算をさらに実行できます。たとえば、分布から cdf を求めたり、乱数を生成することができます。
手順 5. cdf を計算してプロットする。
近似した paretotails 分布の cdf を計算してプロットします。
x = -4:0.01:10; plot(x,cdf(pfit,x))
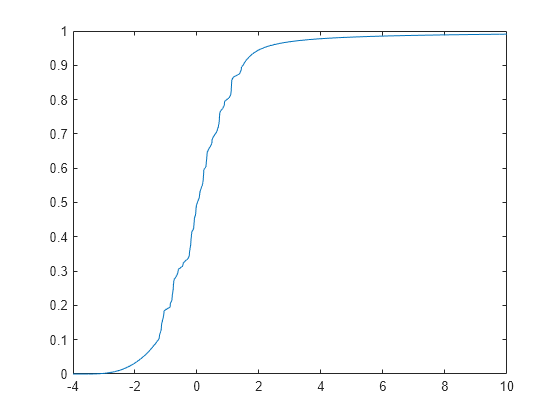
paretotails cdf はデータをよく近似しますが、手順 3 で生成された ecdf よりも裾が滑らかです。
参考
fitdist | paretotails | ecdf