スパース行列
基本的なスパース行列、並べ替えアルゴリズム、反復法、スパース線形代数
スパース行列は、大部分がゼロの double データ、single データ、または logical データを効率的に格納します。"完全な" 行列 ("密行列") は、値に関係なく個々の要素をメモリに保存しますが、"スパース" 行列は 0 以外の要素とその行インデックスだけを保存します。このため、スパース行列を使用すると、データ ストレージに必要なメモリ量を大幅に削減できます。
MATLAB® に内蔵されたすべての代数、論理、インデックス付け演算は、スパース行列、またはスパース行列と完全な行列を組み合わせたものに適用できます。スパース行列での演算はスパース行列を返し、完全な行列での演算は完全な行列を返します。詳細については、スパース行列の計算上の利点およびスパース行列の作成を参照してください。
関数
トピック
- スパース行列の作成
スパース データを行列として保存。
- スパース行列の計算上の利点
完全な行列に対するスパース行列の利点。
- スパース行列へのアクセス
スパース データのインデックス付けと可視化。
- スパース行列の演算
スパース行列による並べ替え、因数分解および計算。
- 線形方程式の反復法
数値線形代数の最も重要で一般的な用途の 1 つは、
A*x = bの形で表せる線形方程式を解くことです。 - スパース行列の並べ替え
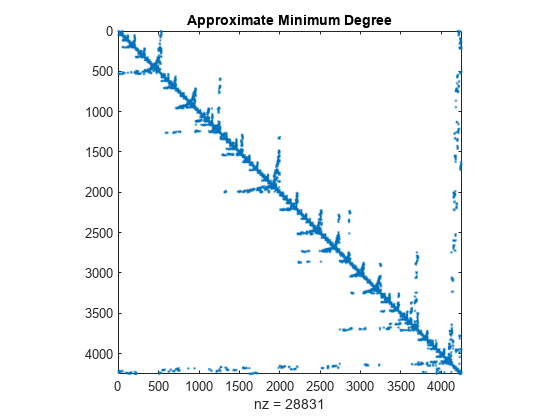
この例では、スパース行列の行と列を並べ替えると、行列操作の要件である速度とストレージにどのような影響を与えるかを示します。