スパース行列の並べ替え
この例では、スパース行列の行と列を並べ替えると、行列操作の要件である速度とストレージにどのような影響を与えるかを示します。
スパース行列の可視化
spy プロットは、行列の非ゼロ要素を示します。
この spy プロットは、バーベル行列の一部から派生するスパース対称正定値行列を示します。この行列は、バーベルに似た形状のグラフ内の接続を記述します。
load barbellgraph.mat S = A + speye(size(A)); pct = 100 / numel(A); spy(S) title('A Sparse Symmetric Matrix') nz = nnz(S); xlabel(sprintf('Nonzeros = %d (%.3f%%)',nz,nz*pct));

以下は、バーベル グラフのプロットです。
G = graph(S,'omitselfloops'); p = plot(G,'XData',xy(:,1),'YData',xy(:,2),'Marker','.'); axis equal
コレスキー因子の計算
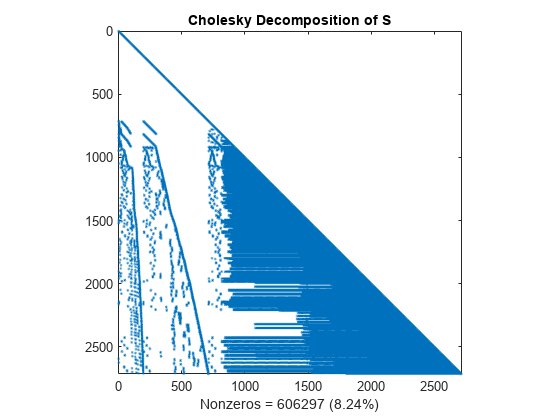
S = L*L' の場合のコレスキー因子 L の計算。コレスキー分解の計算では非スパース (非ゼロ) が発生するため、L には、分解されていない S よりもかなり "多く" の非ゼロ要素が含まれます。これらの非スパース値はアルゴリズム速度を低下させ、ストレージ コストを増加させます。
L = chol(S,'lower'); spy(L) title('Cholesky Decomposition of S') nc(1) = nnz(L); xlabel(sprintf('Nonzeros = %d (%.2f%%)',nc(1),nc(1)*pct));
並べ替えによる計算の高速化
行列の行と列を並べ替えることで、分解で生ずる非スパース要素の量を減らし、それにより以降の計算の時間とストレージ コストを削減できます。
MATLAB® によってサポートされるいくつかの異なる並べ替えを次に示します。
colperm:列カウント法symrcm:逆 Cuthill-McKee 法amd:最小次数法dissect:Nested Dissection
バーベル行列でこれらのスパース行列の並べ替えの効果をテストします。
列カウント並べ替え
colperm コマンドは、列カウント並べ替えアルゴリズムを使用して、非ゼロ要素数のより多い行と列を行列の最後に移動します。
q = colperm(S); spy(S(q,q)) title('S(q,q) After Column Count Ordering') nz = nnz(S); xlabel(sprintf('Nonzeros = %d (%.3f%%)',nz,nz*pct));
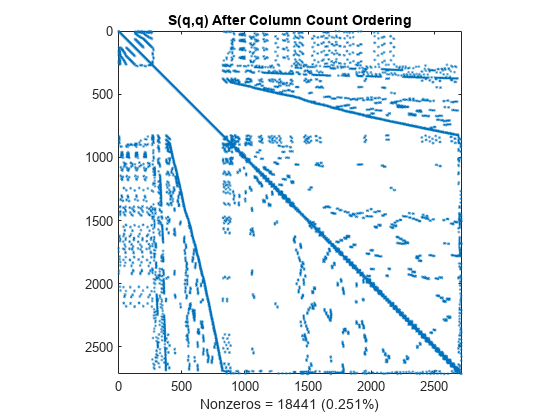
この行列では、列カウント並べ替えによってコレスキー分解の時間とストレージはほとんど削減できません。
L = chol(S(q,q),'lower'); spy(L) title('chol(S(q,q)) After Column Count Ordering') nc(2) = nnz(L); xlabel(sprintf('Nonzeros = %d (%.2f%%)',nc(2),nc(2)*pct));

逆 Cuthill-McKee での並べ替え
symrcm コマンドは、すべての非ゼロ要素を対角要素の近くに移動させ、元の行列のバンド幅を小さくする、逆 Cuthill-McKee 並べ替えアルゴリズムを使用します。
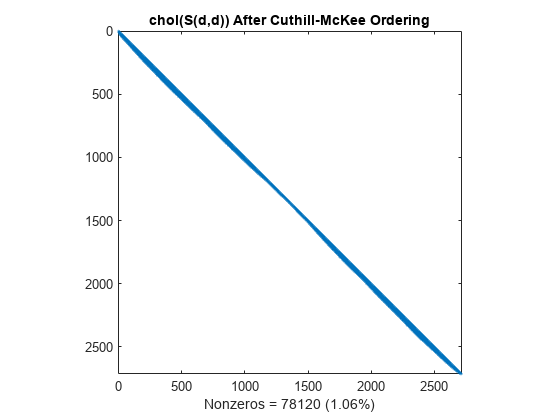
d = symrcm(S); spy(S(d,d)) title('S(d,d) After Cuthill-McKee Ordering') nz = nnz(S); xlabel(sprintf('Nonzeros = %d (%.3f%%)',nz,nz*pct));

並べ替えを行った行列の分解には時間とストレージがあまりかからないように、コレスキー分解によって得られる非スパースは帯上のみに限られます。
L = chol(S(d,d),'lower'); spy(L) title('chol(S(d,d)) After Cuthill-McKee Ordering') nc(3) = nnz(L); xlabel(sprintf('Nonzeros = %d (%.2f%%)', nc(3),nc(3)*pct));
最小次数での並べ替え
amd コマンドは、近似最小次数アルゴリズム (強力なグラフ理論の手法) を使用して、行列の中に大きな 0 のブロックを作成します。
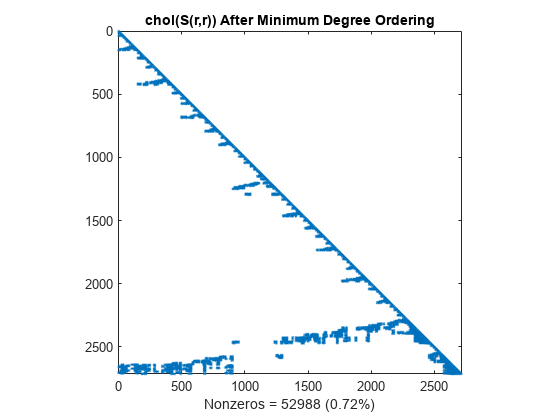
r = amd(S); spy(S(r,r)) title('S(r,r) After Minimum Degree Ordering') nz = nnz(S); xlabel(sprintf('Nonzeros = %d (%.3f%%)',nz,nz*pct));

コレスキー分解は、最小次数アルゴリズムによって得られた 0 のブロックを保持します。この構造により、時間とストレージ コストを大幅に削減できます。
L = chol(S(r,r),'lower'); spy(L) title('chol(S(r,r)) After Minimum Degree Ordering') nc(4) = nnz(L); xlabel(sprintf('Nonzeros = %d (%.2f%%)',nc(4),nc(4)*pct));
Nested Dissection 置換
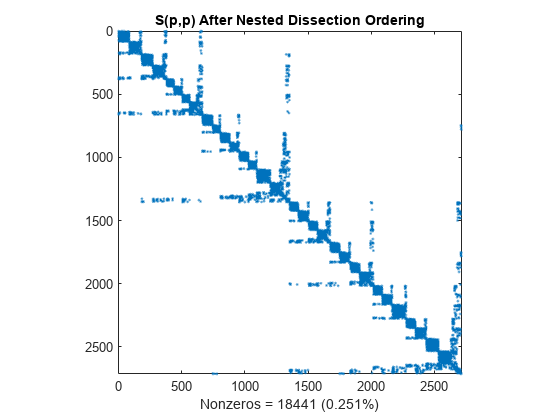
関数 dissect は、グラフ理論の手法を使用して、非ゼロ要素を減らす順序を生成します。このアルゴリズムは行列をグラフの隣接行列として扱い、頂点とエッジを縮約することでグラフを疎化し、小さめのグラフを並べ替えてから、洗練ステップを使用して小さいグラフを密化し、元のグラフの並べ替えを生成します。結果として、他の並べ替えアルゴリズムに比べ、多くの場合に非スパース要素の生成量が最も少ない強力なアルゴリズムとなります。
p = dissect(S); spy(S(p,p)) title('S(p,p) After Nested Dissection Ordering') nz = nnz(S); xlabel(sprintf('Nonzeros = %d (%.3f%%)',nz,nz*pct));
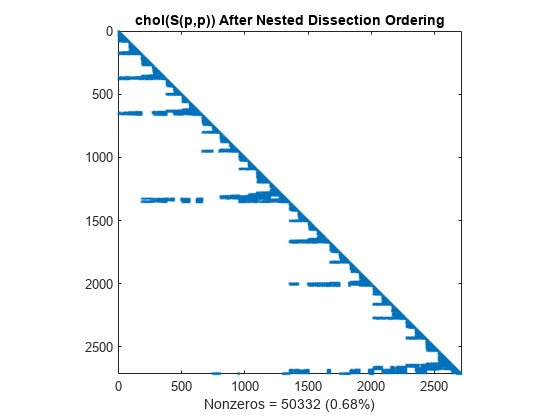
最小次数での並べ替えと同様、Nested Dissection での並べ替えのコレスキー分解では、主対角より下の S(d,d) の非ゼロの構造がほぼ保持されます。
L = chol(S(p,p),'lower'); spy(L) title('chol(S(p,p)) After Nested Dissection Ordering') nc(5) = nnz(L); xlabel(sprintf('Nonzeros = %d (%.2f%%)',nc(5),nc(5)*pct));
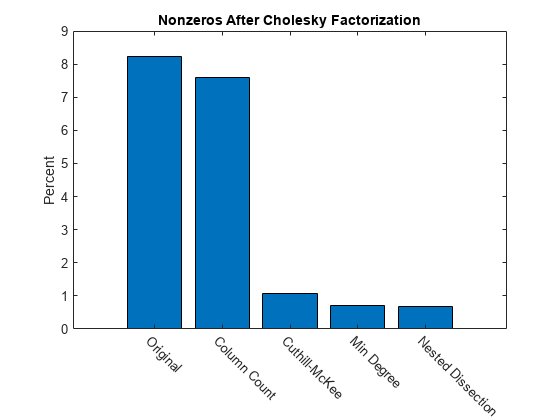
結果のまとめ
この棒グラフは、コレスキー分解を実行する前の行列の並べ替えの効果をまとめています。元の行列のコレスキー分解では要素の約 8% が非ゼロでしたが、dissect または symamd を使用するとその密度は 1% 未満に削減されます。
labels = {'Original','Column Count','Cuthill-McKee',...
'Min Degree','Nested Dissection'};
bar(nc*pct)
title('Nonzeros After Cholesky Factorization')
ylabel('Percent');
ax = gca;
ax.XTickLabel = labels;
ax.XTickLabelRotation = -45;