symrcm

スパース逆 Cuthill-McKee での並べ替え

ページ内をすべて折りたたむ

構文

r = symrcm(S)

説明

r = symrcm(S) は、S の対称逆 Cuthill-McKee での並べ替えを返します。これは、S(r,r) が対角付近に非ゼロ要素をもつような置換ベクトル r です。これは、細長い問題から生じる行列の LU 分解またはコレスキー分解に対して、適切な並べ替えを行います。並べ替えは、S が対称でも非対称でも行われます。

実数対称スパース行列 S に対して、S(r,r) の固有値は、S の固有値と同じですが、eig(S(r,r)) は eig(S) よりも計算時間が短縮されます。

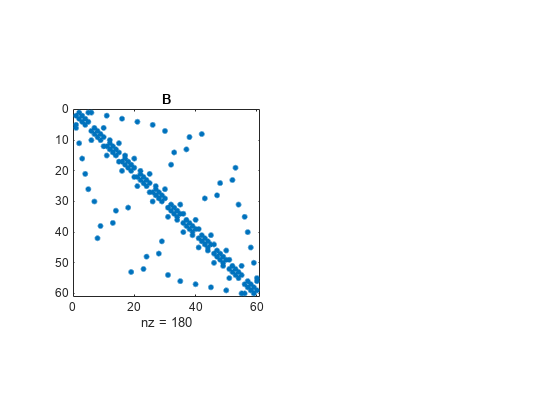
例

すべて折りたたむ

ライブ スクリプトを開く

ステートメント

B = bucky;

は、切り捨て正 20 面体の隣接グラフを生成するために、demos ツールボックス内の関数を使用します。これは、サッカー ボール、Buckminster Fuller の測地線ドーム (このため bucky と呼ばれます)、また最近では 60 原子の炭素分子として知られています。これには、60 個の頂点があります。頂点は、半球面上に現れる頂点の半分の数を使って、5 角形ごとに番号付けられ、それから別の半球面内に射影し、2 つの半球面を張り合わせます。

この番号付けに関しては、最初の spy プロットが示すように、特に幅の狭い行列ではありません。

figure();
subplot(1,2,1),spy(B),title('B')

Figure contains an axes object. The axes object with title B, xlabel nz = 180 contains a line object which displays its values using only markers.

逆 Cuthill-McKeeでの並べ替えは、次のようにして得られます。

p = symrcm(B);
R = B(p,p);

spy プロットは、非常に狭い対角幅を示します。

subplot(1,2,2),spy(R),title('B(p,p)')

Figure contains 2 axes objects. Axes object 1 with title B, xlabel nz = 180 contains a line object which displays its values using only markers. Axes object 2 with title B(p,p), xlabel nz = 180 contains a line object which displays its values using only markers.

この例は、関数 symamd のリファレンス ページに続きます。

対角幅は、次のように計算できます。

[i,j] = find(B);
bw = max(i-j) + 1;

B と R の対角幅は、それぞれ 35 と 12 です。

アルゴリズム

まず、行列のグラフの疑似外周頂点を求めます。その後、breadth-first 検索によってレベル構造を作成し、疑似外周頂点からの距離を小さくすることで頂点を並べ替えます。これは、George と Liu によって書かれた SPARSPAK に基づいて実行されます。

参照

[1] George, Alan and Joseph Liu, Computer Solution of Large Sparse Positive Definite Systems, Prentice-Hall, 1981.

[2] Gilbert, John R., Cleve Moler, and Robert Schreiber, “Sparse Matrices in MATLAB: Design and Implementation,” SIAM Journal on Matrix Analysis, 1992. A slightly expanded version is also available as a technical report from the Xerox Palo Alto Research Center.

拡張機能

すべて展開する

バージョン履歴

R2006a より前に導入

参考

| | |