dissect

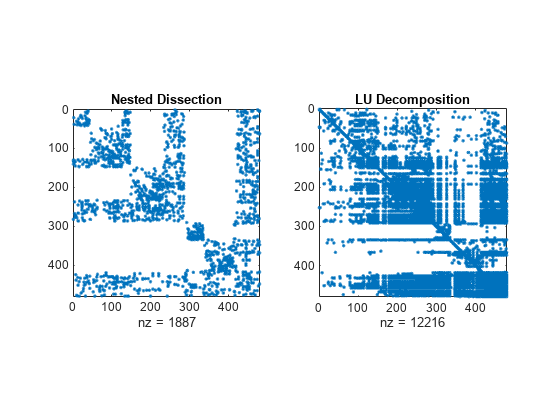
Nested Dissection 置換

構文

p = dissect(A)

p = dissect(A,Name,Value)

説明

p = dissect(A) は、A のスパース構造の Nested Dissection を使用して計算した置換ベクトルを返します。

p = dissect(A,Name,Value) は、1 つ以上の名前と値のペアの引数を使用して追加のオプションを指定します。たとえば、dissect(A,'NumIterations',15) は、Nested Dissection アルゴリズム内で洗練反復を 10 回ではなく、15 回使用します。

例

スパース行列の列の並べ替え

複数のメソッドを使用してスパース行列を並べ替え、並べ替えた行列の LU 分解によって発生した非スパース要素を比較します。

west0479 行列を読み込みます。これは 479 行 479 列の実数値スパース行列であり、共役固有値の実数および複素数のペアをもちます。スパース構造を表示します。

load west0479.mat
A = west0479;
spy(A)

Nested Dissection 順序法を含む複数の異なる方法で、行列の列の置換を計算します。

p1 = dissect(A);
p2 = amd(A);
p3 = symrcm(A);

さまざまな並べ替えメソッドを使用して A の LU 分解のスパース構造を比較します。関数 dissect は、発生する非スパース要素数が最小になる並べ替えを生成します。

subplot(1,2,1)
spy(A)
title('Original Matrix')
subplot(1,2,2)
spy(lu(A))
title('LU Decomposition')

figure
subplot(1,2,1)
spy(A(p3,p3))
title('Reverse Cuthill-McKee')
subplot(1,2,2)
spy(lu(A(p3,p3)))
title('LU Decomposition')

figure
subplot(1,2,1)
spy(A(p2,p2))
title('Approximate Minimum Degree')
subplot(1,2,2)
spy(lu(A(p2,p2)))
title('LU Decomposition')

figure
subplot(1,2,1)
spy(A(p1,p1))
title('Nested Dissection')
subplot(1,2,2)
spy(lu(A(p1,p1)))
title('LU Decomposition')

密な列をフィルター処理で除外

矢印の先端のように非ゼロ要素が配置された行列は、少数の密な列があるスパース行列です。'MaxDegreeThreshold' の名前と値のペアを使用して密な列をフィルター処理し、並べ替えた行列の末尾に配置します。

矢印の先端のように非ゼロ要素が配置されたスパース行列を作成して、スパース パターンを表示します。

A = speye(100) + diag(ones(1,99),1) + diag(ones(1,98),2);
A(1:5,:) = ones(5,100);
A = A + A';
spy(A)

Nested Dissection 順序を計算して、非ゼロ要素が 10 個を超える列をフィルター処理して除外します。

p = dissect(A,'MaxDegreeThreshold',10);

並べ替えた行列のスパース パターンを表示します。dissect は、並べ替えた行列の末尾に密な列を配置します。

spy(A(p,p))

入力引数

A — 入力行列

正方行列

入力行列。正方行列として指定します。A は非スパースまたはスパースのいずれでもかまいません。A が非対称の場合、dissect はそれを対称化します。

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
複素数のサポート: あり

名前と値の引数

引数のオプションのペアを Name1=Value1,...,NameN=ValueN として指定します。ここで Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後になければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、コンマを使用してそれぞれの名前と値を区切り、Name を引用符で囲みます。

例: p = dissect(A,'NumIterations',15,'NumSeparators',2) は、Nested Dissection アルゴリズム内で 15 回の洗練反復と 2 つの区切りを使用します。

VertexWeights — 頂点の重み

ベクトル

頂点の重み。'VertexWeights' とベクトルで構成されるコンマ区切りのペアとして指定します。重みのベクトルは、各頂点に重みが指定されるように、size(A,1) と等しい長さでなければなりません。このオプションを使用して、グラフの頂点 (行列の列) に重みを付ける方法を指定します。これはアルゴリズムが区画間の均衡を計算する方法に影響します。

既定では、Nested Dissection アルゴリズムはすべての頂点に等しく重みを付けます。

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

NumSeparators — 区切りの数

1 (既定値) | 正の整数

区切りの数。'NumSeparators' と正の整数で構成されるコンマ区切りのペアとして指定します。このオプションを使用して、各分割ステップでグラフをいくつの区画に分割するかを指定します。Nested Dissection アルゴリズム内の区切りの数を増加すると、置換の品質が高くなりますが、実行時間が長くなります。

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

NumIterations — 洗練反復の回数

10 (既定値) | 正の整数

洗練反復の回数。'NumIterations' と正の整数で構成されるコンマ区切りのペアとして指定します。洗練反復の数を増加すると、置換の品質が高くなりますが、実行時間が長くなります。

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

MaxImbalance — 区画の不均衡のしきい値

1.2 (既定値) | スカラー

区画の不均衡のしきい値。'MaxImbalance' と、1.001 以上 1.999 以下のスカラー値 (0.001 の整数倍) で構成されるコンマ区切りのペアとして指定します。しきい値を大きくするほど、より低い品質の置換がアルゴリズムで受け入れ可能になり、実行時間が短くなります。

データ型: single | double

MaxDegreeThreshold — 頂点次数のしきい値

0 (既定値) | 非負の整数

頂点次数のしきい値。'MaxDegreeThreshold' と非負の整数で構成されるコンマ区切りのペアとして指定します。Nested Dissection アルゴリズムは、順序付けのときに threshold*(avg degree)/10 より大きい次数をもつ頂点を無視します。dissect はこのように無視された頂点を置換の末尾に配置します。これにより、しきい値より大きい次数をもつすべての頂点が、最初の最上位の区切りの中に効果的に配置されます。フィルター処理により、密接に連結する頂点を除外することで、順序付けの速度と精度が向上する場合があります。

既定値 0 はすべての頂点に順序付けを行うことを意味します。

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

出力引数

p — 置換ベクトル

ベクトル

置換ベクトル。ベクトルとして返されます。インデックス式 A(p,p) で置換ベクトルを使用して、A の列を並べ替えます。たとえば、コレスキー分解 chol(A(p,p)) は、A のコレスキー分解に比べてよりスパースになる傾向があります。

アルゴリズム

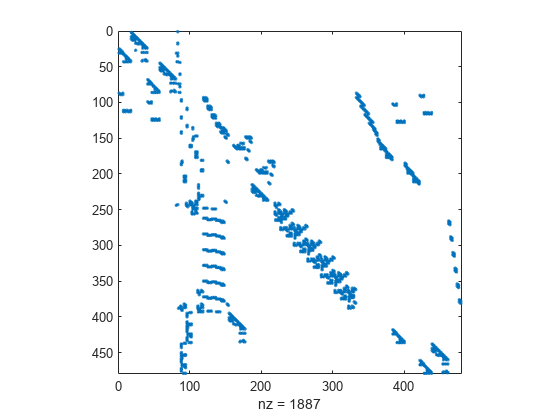
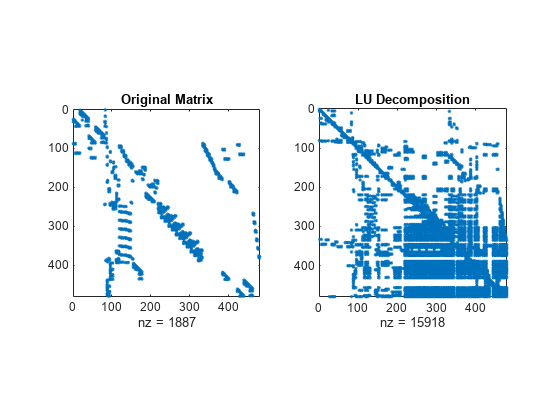
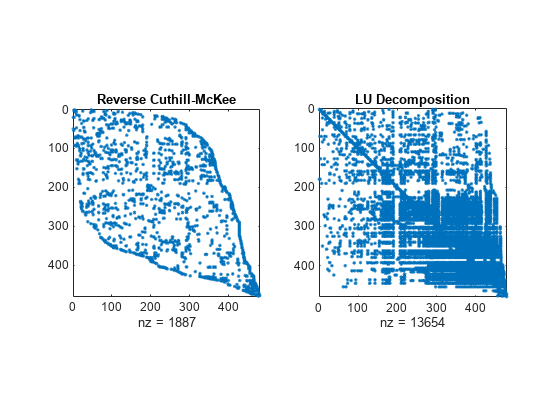
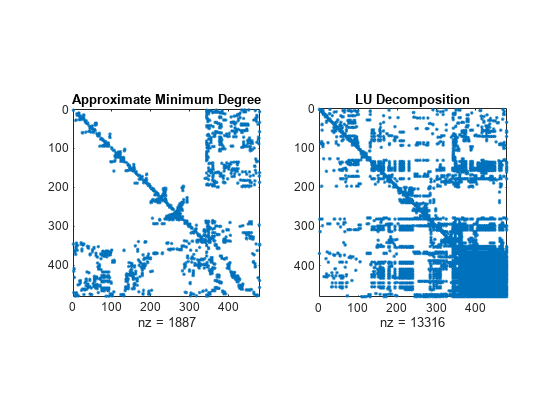
[1]で説明される Nested Dissection 順序法アルゴリズムは、複数レベルのグラフ分割アルゴリズムで、スパース行列の非ゼロ要素を減らす順序付けの生成に使用されます。入力行列は、グラフの隣接行列として扱われます。このアルゴリズムは、頂点とエッジを縮約することでグラフを疎化し、より小さいグラフを並べ替えてから、洗練ステップを使用してその小さいグラフを密化し、元のグラフの並べ替えを生成します。

dissect の名前と値のペアにより、このアルゴリズムのさまざまな段階を制御できます。

• 疎化

  この段階で、アルゴリズムは頂点の隣接ペアをまとめて縮約することで、元のグラフからより小さいグラフを連続して作成します。'MaxDegreeThreshold' を使用して、グラフで連結度の高い頂点 (行列内の密な列) の順序を最後にすることで、これらの頂点をフィルター処理して除外できます。

• 分割

  グラフを疎化した後に、アルゴリズムは小さいグラフをすべて並べ替えます。各分割ステップで、アルゴリズムはグラフを均等な部分に分割しようと試みます。'NumSeparators' はグラフを分割する区画数を指定し、'VertexWeights' はオプションで頂点に重みを割り当て、'MaxImbalance' は異なる区画間の重みの差に関するしきい値を指定します。

• 洗練

  最小のグラフを並べ替えた後に、アルゴリズムは以前まとめた頂点を細分化して投影を行い、グラフを元の大きさのサイズに戻します。各投影ステップの後に、頂点を区画間で移動して解の品質を向上させる洗練ステップを実行します。'NumIterations' はこの密化段階で使用する洗練ステップの数を制御します。

参照

[1] Karypis, George and Vipin Kumar. "A Fast and High Quality Multilevel Scheme for Partitioning Irregular Graphs." SIAM Journal on Scientific Computing. Vol. 20, Number 1, 1999, pp. 359–392.

拡張機能

スレッドベースの環境

MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。

この関数はスレッドベースの環境を完全にサポートしています。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。

バージョン履歴

R2017b で導入

参考

amd | colamd | symamd | symrcm | colperm

トピック

• 置換と並べ替え