amd
近似最小次数の置換
構文
P = amd(A)
P = amd(A,opts)
説明
P = amd(A) は、スパース行列 C = A + A' に対して、近似最小次数による置換ベクトルを返します。コレスキー分解では、C(P,P) または A(P,P) の方が、C または A よりもまばらになる傾向があります。関数 amd は、symamd よりも処理が高速で、関数 symamd よりも返される順列が優れている傾向があります。行列 A は正方でなければなりません。A が完全な行列の場合、amd(A) は、amd(sparse(A)) と同じです。
P = amd(A,opts) では、並べ替えの追加オプションを使用できます。opts 入力は、以下に示す 2 つのフィールドをもつ構造体です。必要なフィールドのみを設定します。
dense — 密と考慮される状態を示す非負のスカラー値。A が n 行 n 列の場合、
A + A'でmax(16,(dense*sqrt(n)))エントリを超える行と列は、「密」と見なされ、順列で無視されます。MATLAB® にて、これらの行と列は、出力置換の最後に置かれます。このオプションが存在しない場合、このフィールドの既定値は 10.0 です。aggressive — アグレッシブ アブソープションを制御するスカラー値。このフィールドが非ゼロ値に設定されている場合、アグレッシブ アブソープションが実行されます。このオプションが存在しない場合、これが既定の設定になります。
MATLAB ソフトウェアは、アセンブリ ツリー ポスト順列を実行します。これは、通常、消去ツリー ポスト順列と同じです。使用される近似度合い更新により、また、「密」と見なされる行と列はポスト順列には関係しないため、必ずしも同じとは限りません。しかし、続いて実行する chol 処理に適しているので、正確な消去ツリー ポスト順列が必要な場合は以下のコードを使用できます。
P = amd(S); C = spones(S)+spones(S'); [ignore, Q] = etree(C(P,P)); P = P(Q);
S が既に対称である場合は、2 行目の C = spones(S)+spones(S') を省略します。
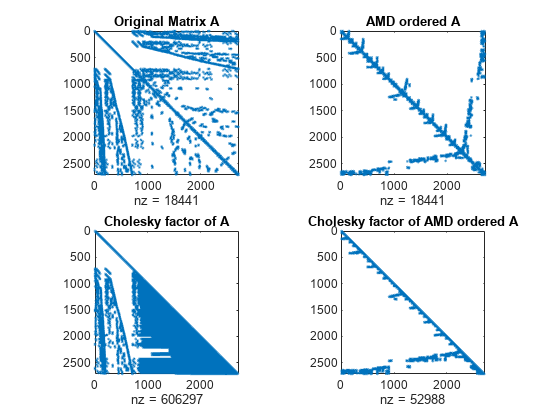
例
参照
[1] Amestoy, Patrick R., Timothy A. Davis, and Iain S. Duff. “Algorithm 837: AMD, an Approximate Minimum Degree Ordering Algorithm.” ACM Transactions on Mathematical Software 30, no. 3 (September 2004): 381–388. https://doi.org/10.1145/1024074.1024081.