スパース行列の演算
処理の効率性
計算量
スパース演算の計算量は、行列内の非ゼロ要素数 nnz に比例します。計算量は、行列の行サイズ m と列サイズ n にも比例します。ただし、ゼロ要素数と非ゼロ要素数の和、すなわち全要素数 m*n には依存していません。
スパース線形方程式の解のようなかなり込み入った演算の量には、前の節で説明した順序付けや密度などの要因が関係しています。ただし、スパース行列演算に要する計算時間は、一般的に非ゼロ数の演算回数に比例します。
アルゴリズムの詳細
スパース行列は以下のルールに従って計算を進めます。
行列を入力するとスカラーまたはベクトルを返す関数は、必ず完全ストレージの書式で出力を作成します。たとえば関数
sizeは、入力が非スパースまたはスパースのどちらであっても常に非スパースのベクトルを返します。スカラーまたはベクトルを入力すると行列を返す
zeros、ones、randおよびeyeなどの関数は常に完全な結果を返します。これは、予期しないスパース性を取り込まないようにするためです。zeros(m,n)のスパース行列は、単にsparse(m,n)です。関数rand、関数eyeのスパース行列バージョンは、それぞれsprand,speyeです。関数onesのスパース行列バージョンはありません。行列を入力して行列またはベクトルを返す単項関数は、オペランドのストレージ クラスを保存します。
Sがスパース行列の場合、chol(S)もスパース行列で、diag(S)はスパースベクトルです。関数maxや関数sumなどの列方向に機能する関数は、これらのベクトルがすべて非ゼロでもスパース ベクトルを返します。このルールが適用されない関数の例外は、関数sparseおよび関数fullです。二項演算子は、両方のオペランドがスパースの場合はスパースを出力し、両方のオペランドが非スパースの場合は非スパースを出力します。非スパースとスパースが混在したオペランドの場合は、演算がスパース性を保存しない限り、結果は非スパースになります。
SがスパースでFが非スパースの場合、S+F、S*F、F\Sは非スパースに、S.*F、S&Fはスパースになります。行列にゼロ要素がほとんど含まれないにもかかわらず、結果がスパースになる場合もあります。関数
catまたは大かっこのいずれかを使って行列の連結を行うと、非スパースとスパースの混合オペランドに対する出力はスパース性をもちます。
置換と並べ替え
スパース行列 S の行と列の置換は、2 つの方法により表現されます。
置換行列
Pは、P*SとしてSの行に、またはS*P'として列に作用します。置換ベクトル
pは、1:nの置換を含む非スパースのベクトルですが、これはS(p,:)としてSの行に、またはS(:,p)として列に作用します。
以下に例を示します。
p = [1 3 4 2 5] I = eye(5,5); P = I(p,:) e = ones(4,1); S = diag(11:11:55) + diag(e,1) + diag(e,-1)
p =
1 3 4 2 5
P =
1 0 0 0 0
0 0 1 0 0
0 0 0 1 0
0 1 0 0 0
0 0 0 0 1
S =
11 1 0 0 0
1 22 1 0 0
0 1 33 1 0
0 0 1 44 1
0 0 0 1 55置換ベクトル p と置換行列 P を使って、いくつかの置換を行うことができます。たとえば、ステートメント S(p,:) と P*S は同じ行列を返します。
S(p,:)
ans =
11 1 0 0 0
0 1 33 1 0
0 0 1 44 1
1 22 1 0 0
0 0 0 1 55P*S
ans =
11 1 0 0 0
0 1 33 1 0
0 0 1 44 1
1 22 1 0 0
0 0 0 1 55同様に、S(:,p) と S*P' は両方とも以下を生成します。
S*P'
ans =
11 0 0 1 0
1 1 0 22 0
0 33 1 1 0
0 1 44 0 1
0 0 1 0 55P がスパース行列の場合、この 2 つの表現は n に比例したストレージを使い、計算時間は nnz(S) に比例します。S に対してどちらの方法でも適用できます。ベクトル表現の方が、わずかですがコンパクトで効率的であるため、さまざまなスパース行列置換ルーチンは、すべて完全な行ベクトルを返します。ただし、LU (三角) 分解のピボット置換 (これは、MATLAB の古いバージョンと互換性のある行列を出力) のみが例外です。
2 つの置換の表現を変換するには、次のようにします。
n = 5; I = speye(n); Pr = I(p,:); Pc = I(:,p); pc = (1:n)*Pc
pc =
1 3 4 2 5pr = (Pr*(1:n)')'
pr =
1 3 4 2 5P の逆変換は R = P' です。p の逆変換は r(p) = 1:n で計算できます。
r(p) = 1:5
r =
1 4 2 3 5スパース性を高める並べ替え
行列の列を並べ替えることによって、LU または QR 因子のスパース性を強くすることができます。行と列を並べ替えると、コレスキー因子のスパース性が強くなる場合がよくあります。最も簡単な並べ替えは、非ゼロ要素数別に列を並べ替える方法です。これは非常に不規則な構造をもつ行列を並べ替える場合、特に非ゼロの行数または列数に大きな差がある場合に有効な方法となることがあります。
colperm は、行列の列を各列内の非ゼロの数に基づいて最小値から最大値の順への並べ替えを計算します。
バンド幅を狭くするための並べ替え
逆 Cuthill-McKee 法は、行列のプロファイルまたはバンド幅を狭くするためのものです。最小バンド幅の検出を保証するものではありませんが、一般的に使われています。関数 symrcm は実際には、対称行列 A + A' の非ゼロの構造体に機能しますが、出力結果は非対称行列に対しても使用できます。この順序付けは 1 次元の問題や "細長い" 問題の行列に効果的です。
近似最小次数順序
グラフのノード次数は、そのノードの結合数で示されます。これは隣接行列の対応する行において、非対角部分の非ゼロ要素数と同数になります。近似最小次数アルゴリズムは、これらの次数がガウスの消去法またはコレスキー分解の中で、どのように次数が変更されていくかをベースにした順序付けを行います。これは列カウンターや逆 Cuthill-McKee などの、他のほとんどの順序付けよりも強いスパース係数をもたらす複雑で強力なアルゴリズムです。各ノードの次数の記録を保持すると、時間を浪費するので、近似最小次数アルゴリズムは厳密な次数ではなく、次数の近似を使用します。
これらの MATLAB® 関数は、近似最小次数アルゴリズムを実装します。
symamd を使用する例は、スパース行列の並べ替えと分解を参照してください。
関数 spparms を使うと、アルゴリズムの詳細に関連するさまざまなパラメーターを変更することができます。
関数 colamd および symamd で使用されるアルゴリズムの詳細は、[5] を参照してください。アルゴリズムで使用される近似次数は、[1] に基づいています。
Nested Dissection 順序
近似最小次数順序と同様に、関数 dissect によって実装される Nested Dissection 順序アルゴリズムは、この行列がグラフの隣接行列となることを考慮して、行列の行と列を並べ替えます。このアルゴリズムは、グラフ内の頂点のペアを共に折りたたむことにより、問題の規模を大幅に縮小します。小さいグラフを並べ替えた後に、アルゴリズムは投影と調整のステップを適用して、グラフを元のサイズに拡張します。
Nested Dissection アルゴリズムでは、質の高い並べ替えが可能であり、特に有限要素行列を扱う場合に他の並べ替え手法よりも優れた機能を発揮します。Nested Dissection 順序アルゴリズムの詳細については、[7]を参照してください。
スパース行列の因数分解
LU 分解
S がスパース行列の場合、次のコマンドは 3 つのスパース行列 L, U, P を返します。ここで、この行列には P*S = L*U の関係があります。
[L,U,P] = lu(S);
lu は、部分ピボットを使ったガウスの消去法で因子を取得します。置換行列 P には n 個の非ゼロ要素のみが含まれます。密行列と同様に、ステートメント [L,U] = lu(S) は置換された単位下三角行列と上三角行列を返し、その積は S になります。出力引数なしの場合、lu(S) はピボット情報をもたない単一行列として、L および U を返します。
3 出力の構文 [L,U,P] = lu(S) は、数値部分ピボットにより P を選択しますが、LU 因子のスパース性を高めるためのピボット操作は行いません。一方、4 出力の構文 [L,U,P,Q] = lu(S) は、しきい値部分ピボットに対して P を選択し、LU 因子でスパース性を高めるために、P と Q を選択します。
次のコマンドを使って、スパース行列内のピボットを制御することができます。
lu(S,thresh)
ここで、thresh は [0,1] の範囲内のピボットしきい値です。ピボット操作は、ある列の対角要素の大きさが、その列内の 1 つ下の対角要素の thresh 倍よりも小さい場合に生じます。thresh = 0 は対角ピボット操作を強制します。既定は thresh = 1 です (4 出力の構文に対して、thresh の既定は 0.1 です)。
lu を 3 出力以下で呼び出す場合、MATLAB は分解の間、スパースの L と U の係数を保持するために必要なメモリを自動的に割り当てます。4 出力の構文の場合を除き、MATLAB はシンボリックな LU 事前分解を使って事前に必要なメモリを決め、データ構造を設定することはありません。
スパース行列の並べ替えと分解
この例では、並べ替えと分解がスパース行列に及ぼす影響について説明します。
非スパース要素を減らす適切な列置換 p を、symrcm や colamd などから入手する場合は、lu(S(:,p)) の計算に要する時間とストレージが、lu(S) の計算より少なくなります。
バッキー ボールの例を使用して、スパース行列を作成します。
B = bucky;
B の各行、各列には、厳密に 3 つの非ゼロ要素があります。
2 つの置換 r および m を、それぞれ symrcm と symamd を使用して作成します。
r = symrcm(B); m = symamd(B);
この 2 つの置換は、対称逆 Cuthill-McKee での並べ替えと、対称な近似最小次数の並べ替えです。
これら 3 つの異なる番号付けをもつ、バッキー ボール グラフの 3 つの隣接行列を表示する spy プロットを作成します。オリジナルの番号付けによる、ローカルの五角形ベースの構造は、他では明らかになりません。
figure subplot(1,3,1) spy(B) title('Original') subplot(1,3,2) spy(B(r,r)) title('Reverse Cuthill-McKee') subplot(1,3,3) spy(B(m,m)) title('Min Degree')
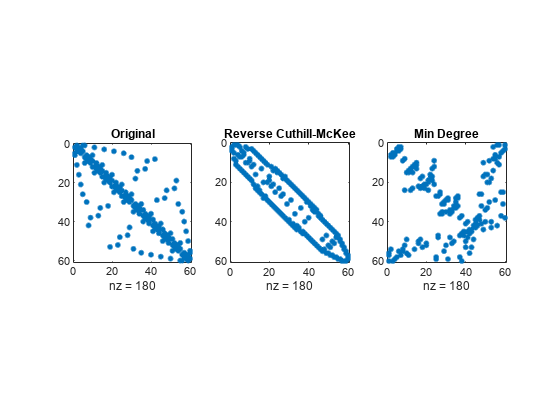
逆 Cuthill-McKee での並べ替え r は、帯域幅を小さくし、すべての非ゼロ要素を対角付近に集中させます。近似最小次数順序 m は、大きな 0 のブロックを伴うフラクタル状の構造を生み出します。
バッキー ボールの LU 分解で生成された非ゼロ要素を確認するには、スパース単位行列 speye を使用して、B の対角に -3 を挿入します。
B = B - 3*speye(size(B));
各行の合計がゼロになるため、この新しい B は実際は特異行列ですが、それでもその LU 分解を計算することは有益です。出力引数を 1 つだけ指定して呼び出すと、lu は、L と U の 2 つの三角因子を 1 つのスパース行列で返します。この行列内の非ゼロの数は、B を含む線形システムを解くために必要な時間とストレージの目安になります。
考察対象となっている 3 つの置換での非ゼロの数は次のとおりです。
lu(B)(オリジナル): 1022lu(B(r,r))(逆 Cuthill-McKee): 968lu(B(m,m))(近似最小次数): 636
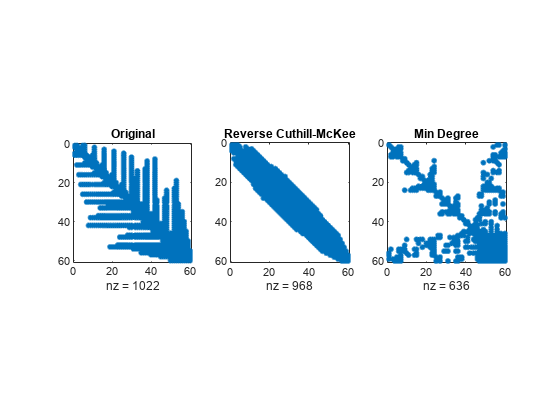
これは小規模な例ですが、結果は典型的なものです。オリジナルの番号付けスキームで非ゼロ要素が最も多くなっています。逆 Cuthill-McKee での並べ替えの非ゼロ要素は帯域内に集中していますが、最初の 2 つの並べ替えとほぼ同じくらい広範囲に渡っています。近似最小次数順序では、比較的大きい 0 のブロックが消去時に保持されており、非ゼロ要素の数は、他の並べ替えで生成された数に比べ大幅に少なくなっています。
以下の spy プロットは、それぞれの並べ替えの特性を反映しています。
figure subplot(1,3,1) spy(lu(B)) title('Original') subplot(1,3,2) spy(lu(B(r,r))) title('Reverse Cuthill-McKee') subplot(1,3,3) spy(lu(B(m,m))) title('Min Degree')
コレスキー分解
S が対称 (またはエルミート)、正定値、スパース行列の場合、次のステートメントは R'*R = S を満たす上三角スパース行列 R を返します。
R = chol(S)
chol はスパースに対しては自動的にピボットを行いませんが、chol(S(p,p)) に対して最小次数を計算し、制約付き置換をプロファイルします。
コレスキー アルゴリズムはスパース性にはピボットを使わず、数値的安定性にもピボットを必要としないため、chol は分解の最初に必要なメモリの総量を迅速に計算し、すべてのメモリを割り当てます。symbfact を使って、すなわち chol と同じアルゴリズムを使って、必要なメモリ割り当てを計算できます。
QR 分解
MATLAB は、次のステートメントでスパース行列 S の完全な QR 分解を行います。
[Q,R] = qr(S)
[Q,R,E] = qr(S)
ただし、多くの場合現実的なものではありません。ユニタリ行列 Q では、ゼロ要素の割合を大きくできない場合がよくあります。より実際的な方法、いわゆる「Q-less QR 分解」として知られている方法を使用できます。
次のように 1 つのスパース行列を入力引数とし、1 つの出力引数を設定すると、
R = qr(S)
QR 分解の上三角行列のみを返します。行列 R は、次の正規方程式に従って行列にコレスキー分解をした結果です。
R'*R = S'*S
ただし、S'*S の計算に内在する数値的情報の欠落は回避されます。
同じ行数をもつ 2 つの入力引数と 2 つの出力引数を設定すると、
[C,R] = qr(S,B)
は B に直交変換を適用し、Q を計算しないで C = Q'*B を出力します。
Q-less QR 分解は、スパース最小二乗問題
の解を、次の 2 ステップで出力します。
[c,R] = qr(A,b); x = R\c
A がスパースで正方でない場合、MATLAB はバックスラッシュ演算子で線形方程式を解きます。
x = A\b
または独自に分解を行い、R のランク落ちをチェックします。
異なる右辺 b をもつ最小二乗線形方程式を連続して解くこともできます。b は R = qr(A) が計算されるとき、必ずしも既知ではありません。このアプローチでは、次により "準正規方程式 R'*R*x = A'*b を解きます。
x = R\(R'\(A'*b))
そして丸め誤差を低減するために反復計算を行います。
r = b - A*x; e = R\(R'\(A'*r)); x = x + e
不完全分解
関数 ilu と関数 ichol は、近似 "不完全" 分解を行います。これはスパース反復法の前処理行列として便利です。
関数 ilu は 3 つの "不完全上下" (ILU) 分解を行います。以下の 3 種類になります。"ゼロで埋める ILU" (ILU(0))、Crout バージョンの ILU (ILUC(tau))、および棄却とピボットのしきい値をもつ ILU (ILUTP(tau))。ILU(0) は決してピボットせず、結果の因数は入力行列に非ゼロ要素がある位置に非ゼロ要素のみをもちます。ただし、ILUC(tau) と ILUTP(tau) は両方ともユーザー定義の棄却許容誤差 tau によるしきい値ベースの棄却を実行します。
以下に例を示します。
A = gallery('neumann',1600) + speye(1600);
nnz(A)ans =
7840nnz(lu(A))
ans =
126478A は 7840個の非ゼロ要素をもち、その完全 LU 分解は 126478 個の非ゼロ要素をもちます。また、次のコードは別の ILU 出力を示します。
[L,U] = ilu(A); nnz(L)+nnz(U)-size(A,1)
ans =
7840norm(A-(L*U).*spones(A),'fro')./norm(A,'fro')
ans = 4.8874e-17
opts.type = 'ilutp';
opts.droptol = 1e-4;
[L,U,P] = ilu(A, opts);
nnz(L)+nnz(U)-size(A,1)ans =
31147norm(P*A - L*U,'fro')./norm(A,'fro')
ans = 9.9224e-05
opts.type = 'crout';
[L,U,P] = ilu(A, opts);
nnz(L)+nnz(U)-size(A,1)ans =
31083norm(P*A-L*U,'fro')./norm(A,'fro')
ans = 9.7344e-05
これらの計算はゼロで埋められた因数が 7840 個の非ゼロ要素をもち、ILUTP(1e-4) 因数が 31147 個の非ゼロ要素をもち、ILUC(1e-4) 因数が 31083 個の非ゼロ要素をもつことを示します。また、ゼロで埋められた因数の積の関連エラーは、A のパターンでは、基本的にゼロです。最後に、棄却のしきい値によって生成される関連エラーは、棄却許容誤差と同じ順序にありますが、これは発生が保証されません。詳細や他のオプションについては、ilu のリファレンス ページを参照してください。
関数 ichol は、対称、正定値スパース行列の"ゼロで埋められた不完全コレスキー分解" (IC(0)) および棄却しきい値ベースの不完全コレスキー分解 (ICT(tau)) を提供します。これらの分解は、上記の不完全 LU 分解に似ており、同じ特徴が多数あります。以下に例を示します。
A = delsq(numgrid('S',200));
nnz(A)ans =
195228nnz(chol(A,'lower'))ans =
7762589A は 195228 個の非ゼロ要素をもち、並べ替えなしの完全コレスキー分解により、非ゼロ要素が 7762589 個になります。反対にL = ichol(A); nnz(L)
ans =
117216norm(A-(L*L').*spones(A),'fro')./norm(A,'fro')
ans = 3.5805e-17
opts.type = 'ict';
opts.droptol = 1e-4;
L = ichol(A,opts);
nnz(L)ans =
1166754norm(A-L*L','fro')./norm(A,'fro')
ans = 2.3997e-04
IC(0) は、A の下三角行列のパターンでのみ非ゼロ要素をもち、A のパターンで因数の積が一致します。また、ICT(1e-4) 因数は完全コレスキー因数よりも大幅にスパースであり、A と L*L' の間の関連エラーは、棄却許容誤差と同じ順序です。chol で提供される因数と違って、ichol で提供される既定の因数は下三角行列であることに注意することが重要です。詳細については、ichol のリファレンス ページを参照してください。
固有値と特異値
以下の 2 つの関数は、少数の特殊な固有値または特異値の計算に使用できます。関数 svds は eigs をベースにしています。
これらの関数はスパース行列と共に頻繁に使われるものです。ただし、完全な行列でも使用でき、MATLAB コードで定義される線形演算子と共に使用できます。
ステートメント
[V,lambda] = eigs(A,k,sigma)
は、"シフト" sigma の近傍にある行列 A の k 個の固有値と対応する固有ベクトルを検出します。sigma を省略すると、大きさが最大の固有値を探します。sigma がゼロの場合、最小の大きさの固有値を探します。次のように 2 番目の行列 B が、一般化固有値問題に含まれます。Aυ = λBυ
ステートメント
[U,S,V] = svds(A,k)
は、A の k 個の最大特異値を求め、
[U,S,V] = svds(A,k,'smallest')
は、k 個の最小特異値を出力します。
関数 eigs および関数 svds で使用される数値的な技法は、[6] で説明されています。
スパース行列の最小の固有値
この例では、スパース行列の最小の固有値と固有ベクトルを見出す方法を説明します。
L 型 2 次元領域の 65 行 65 列のグリッドで、5 点のラプラシアン差分演算子を設定します。
L = numgrid('L',65);
A = delsq(L);非ゼロ要素の順序と数を決定します。
size(A)
ans = 1×2
2945 2945
nnz(A)
ans = 14473
A は、14,473 個の非ゼロ要素を含む、次数 2945 の行列です。
最小の固有値と固有ベクトルを計算します。
[v,d] = eigs(A,1,'smallestabs');固有ベクトルの成分を適切なグリッド点に分布させ、結果の等高線図を生成します。
L(L>0) = full(v(L(L>0)));
x = -1:1/32:1;
contour(x,x,L,15)
axis square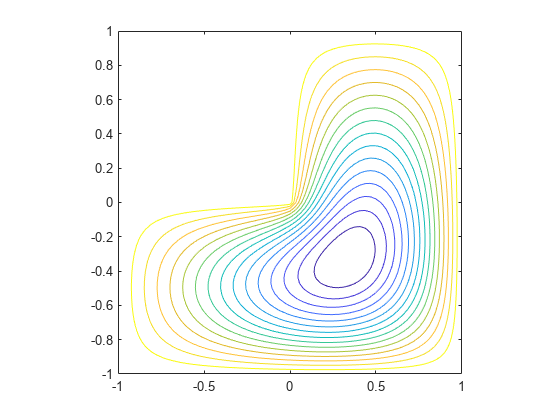
参照
[1] Amestoy, P. R., T. A. Davis, and I. S. Duff, “An Approximate Minimum Degree Ordering Algorithm,” SIAM Journal on Matrix Analysis and Applications, Vol. 17, No. 4, Oct. 1996, pp. 886-905.
[2] Barrett, R., M. Berry, T. F. Chan, et al., Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, SIAM, Philadelphia, 1994.
[3] Davis, T.A., Gilbert, J. R., Larimore, S.I., Ng, E., Peyton, B., “A Column Approximate Minimum Degree Ordering Algorithm,” Proc. SIAM Conference on Applied Linear Algebra, Oct. 1997, p. 29.
[4] Gilbert, John R., Cleve Moler, and Robert Schreiber, “Sparse Matrices in MATLAB: Design and Implementation,” SIAM J. Matrix Anal. Appl., Vol. 13, No. 1, January 1992, pp. 333-356.
[5] Larimore, S. I., An Approximate Minimum Degree Column Ordering Algorithm, MS Thesis, Dept. of Computer and Information Science and Engineering, University of Florida, Gainesville, FL, 1998.
[6] Saad, Yousef, Iterative Methods for Sparse Linear Equations. PWS Publishing Company, 1996.
[7] Karypis, George and Vipin Kumar. "A Fast and High Quality Multilevel Scheme for Partitioning Irregular Graphs." SIAM Journal on Scientific Computing. Vol. 20, Number 1, 1999, pp. 359–392.