ichol
不完全コレスキー分解
説明
例
この例では、修正不完全コレスキー分解を生成します。
対称正定値行列 A から始めます。
N = 100;
A = delsq(numgrid('S',N));A は、Dirichlet 境界条件による 100 行 100 列の正方形グリッド上の負の 2 次元 5 点分散ラプラシアンです。A のサイズは 98*98 = 9604 となります (グリッドの境界がディリクレ条件を課すために使用されるので、10,000 ではない)。
埋め込みなしの不完全コレスキー分解は、A が非ゼロを含むため、同じ位置に非ゼロのみを含む分解です。このような分解は、算出が非常に容易です。積 L*L' は一般に、A とは大きく異なりますが、積 L*L' は該当するパターンで A と一致します (丸めを除く)。
L = ichol(A); norm(A-L*L','fro')./norm(A,'fro')
ans = 0.0916
norm(A-(L*L').*spones(A),'fro')./norm(A,'fro')
ans = 4.9606e-17
また、ichol を使用して、しきい値棄却による不完全コレスキー分解を実行することもできます。棄却許容誤差が小さくなると、係数は密になり、積 L*L' はより優れた A の近似となる傾向があります。以下のプロットは、完全コレスキー係数の密度に対する不完全係数の密度の割合と、棄却許容誤差に対してプロットした不完全分解の相対誤差を示します。
n = size(A,1); ntols = 20; droptol = logspace(-8,0,ntols); nrm = zeros(1,ntols); nz = zeros(1,ntols); nzComplete = nnz(chol(A,'lower')); for k = 1:ntols L = ichol(A,struct('type','ict','droptol',droptol(k))); nz(k) = nnz(L); nrm(k) = norm(A-L*L','fro')./norm(A,'fro'); end figure loglog(droptol,nrm,'LineWidth',2) title('Drop tolerance vs norm(A-L*L'',''fro'')./norm(A,''fro'')')
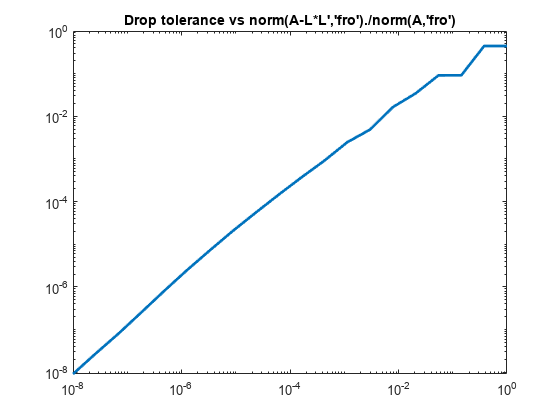
figure semilogx(droptol,nz./nzComplete,'LineWidth',2) title('Drop tolerance vs fill ratio ichol/chol')
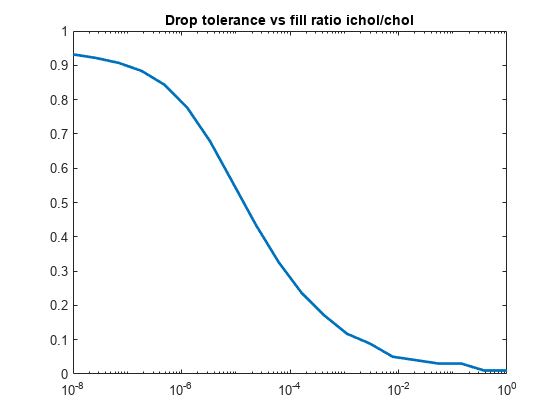
相対誤差は通常、棄却許容誤差と同じ次元にありますが、必ず同じとは保証できません。
この例では、収束を改善するための前処理行列として、不完全コレスキー分解を使用する方法を説明します。
対称正定値行列 A を作成します。
N = 100;
A = delsq(numgrid('S',N));不完全コレスキー分解を pcg の前処理行列として作成します。定数ベクトルを右側に使用します。ベースラインとして、前処理行列なしで pcg を実行します。
b = ones(size(A,1),1); tol = 1e-6; maxit = 100; [x0,fl0,rr0,it0,rv0] = pcg(A,b,tol,maxit);
fl0 = 1 は、pcg が最大許容反復回数内で相対残差を要求した許容誤差に収めないことを示します。埋め込みなしの不完全コレスキー分解を前処理行列として試行します。
L1 = ichol(A); [x1,fl1,rr1,it1,rv1] = pcg(A,b,tol,maxit,L1,L1');
fl1 = 0 は、pcg が反復 59 回で要求した許容誤差に収束することを示します (it1 の値)。この行列はラプラシアンで離散化されていますが、変更済みの不完全コレスキーを使用すると、より良好な前提条件を作成できます。変更済みの不完全コレスキー分解は、演算子の処理を定数ベクトルに保持する近似分解を構築します。すなわち、norm(A*e-L*(L'*e)) は、norm(A-L*L','fro')/norm(A,'fro') がゼロ近傍でない場合でも、e = ones(size(A,2),1) でほぼゼロになります。nofill が既定であるため、この構文ではタイプを指定する必要はありませんが、指定することをお勧めします。
options.type = 'nofill'; options.michol = 'on'; L2 = ichol(A,options); e = ones(size(A,2),1); norm(A*e-L2*(L2'*e))
ans = 3.7983e-14
[x2,fl2,rr2,it2,rv2] = pcg(A,b,tol,maxit,L2,L2');
pcg はわずか 38 回の反復で収束します (fl2 = 0)。3 つの収束履歴をすべてプロットすると、以下の収束が得られます。
semilogy(0:maxit,rv0./norm(b),'b.'); hold on semilogy(0:it1,rv1./norm(b),'r.'); semilogy(0:it2,rv2./norm(b),'k.'); legend('No Preconditioner','IC(0)','MIC(0)');
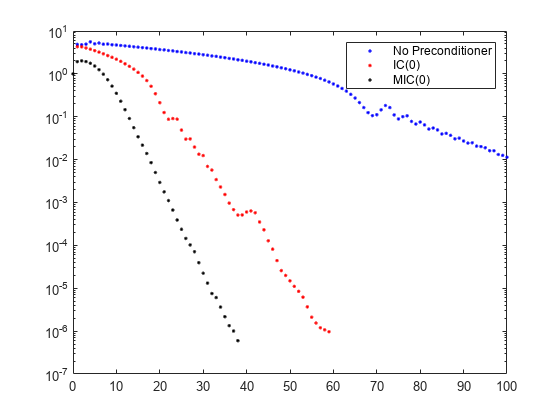
このプロットは、変更済み不完全コレスキー前提条件がより速く収束を達成することを示します。
また、しきい値棄却による不完全コレスキー分解を試行することもできます。以下のプロットは、各種の棄却許容誤差で構築した前処理行列による pcg の収束を示します。
L3 = ichol(A, struct('type','ict','droptol',1e-1)); [x3,fl3,rr3,it3,rv3] = pcg(A,b,tol,maxit,L3,L3'); L4 = ichol(A, struct('type','ict','droptol',1e-2)); [x4,fl4,rr4,it4,rv4] = pcg(A,b,tol,maxit,L4,L4'); L5 = ichol(A, struct('type','ict','droptol',1e-3)); [x5,fl5,rr5,it5,rv5] = pcg(A,b,tol,maxit,L5,L5'); figure semilogy(0:maxit,rv0./norm(b),'b-','linewidth',2); hold on semilogy(0:it3,rv3./norm(b),'b-.','linewidth',2); semilogy(0:it4,rv4./norm(b),'b--','linewidth',2); semilogy(0:it5,rv5./norm(b),'b:','linewidth',2); legend('No Preconditioner','ICT(1e-1)','ICT(1e-2)', ... 'ICT(1e-3)','Location','SouthEast');
棄却許容誤差 1e-2 で構築した不完全コレスキー前処理行列は、ICT(1e-2) となります。
行列が楕円型偏微分方程式に基づくため、ゼロ埋め込み不完全コレスキーと同じように、しきい値棄却分解も変更により効果を上げることができます (すなわち options.michol = 'on')。MIC(0) と同様に、変更済みしきい値ベース棄却不完全コレスキーは、前処理行列の処理を定数ベクトルに保持します。すなわち、norm(A*e-L*(L'*e)) はほぼゼロとなります。
この例では、ichol の diagcomp オプションの使用方法を説明します。
正定値行列の不完全コレスキー分解は、常に存在するわけではありません。以下のコードでは、乱数対称正定値行列を構築し、pcg を使用して線形システムを解きます。
S = rng('default');
A = sprandsym(1000,1e-2,1e-4,1);
rng(S);
b = full(sum(A,2));
[x0,fl0,rr0,it0,rv0] = pcg(A,b,1e-6,100);収束が達成されていないため、不完全コレスキー前処理行列の作成を試行します。
L = ichol(A,struct('type','ict','droptol',1e-3));
Error using ichol Encountered nonpositive pivot.
ichol が前述のように分解される場合、diagcomp オプションを使用して、シフトされた不完全コレスキー分解を構築できます。すなわち、L を構築するのではなく、L*L' が A を近似すること、対角補正の ichol が L を構築し、L*L' が明示的に M を形成することなく M = A + alpha*diag(diag(A)) を近似することを意味します。対角優位の行列では不完全分解が常に存在するため、alpha を見つけて M を対角優位にすることができます。
alpha = max(sum(abs(A),2)./diag(A))-2
alpha = 62.9341
L1 = ichol(A, struct('type','ict','droptol',1e-3,'diagcomp',alpha)); [x1,fl1,rr1,it1,rv1] = pcg(A,b,1e-6,100,L1,L1');
ここで、pcg はまだ、指定の反復回数内に必要な許容誤差に収束することができませんが、pcg では、前処理行列なしよりも、この前処理行列のほうが良好な収束が得られています。alpha を小さくすると有効な場合があります。実験をある程度行うと、alpha の適切な値を得ることができます。
alpha = .1; L2 = ichol(A, struct('type','ict','droptol',1e-3,'diagcomp',alpha)); [x2,fl2,rr2,it2,rv2] = pcg(A,b,1e-6,100,L2,L2');
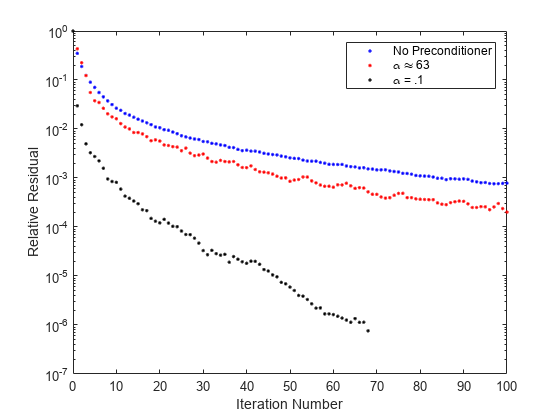
これで、pcg が収束し、プロットには各前処理行列の収束履歴が示されます。
semilogy(0:100,rv0./norm(b),'b.'); hold on; semilogy(0:100,rv1./norm(b),'r.'); semilogy(0:it2,rv2./norm(b),'k.'); legend('No Preconditioner','\alpha \approx 63','\alpha = .1'); xlabel('Iteration Number'); ylabel('Relative Residual');
入力引数
ヒント
参照
[1] Saad, Yousef. “Preconditioning Techniques.” Iterative Methods for Sparse Linear Systems. PWS Publishing Company, 1996.
[2] Manteuffel, T.A. “An incomplete factorization technique for positive definite linear systems.” Math. Comput. 34, 473–497, 1980.
