このページの翻訳は最新ではありません。ここをクリックして、英語の最新版を参照してください。

ilu

不完全 LU 分解

構文

[L,U] = ilu(A)

[L,U,P] = ilu(A)

W = ilu(A)

[___] = ilu(A,options)

説明

[L,U] = ilu(A) は、ゼロ埋め込みを使用してスパース行列 A の不完全 LU 分解を実行し、下三角行列 L と上三角行列 U を返します。

[L,U,P] = ilu(A) はさらに、L と U が P*A または A*P の不完全因子となる置換行列 P を返します。既定では、P はピボットなしの不完全 LU 分解の単位行列です。

W = ilu(A) は、LU 因子の非ゼロ要素を返します。出力 W は L + U - speye(size(A)) と等しくなります。

[___] = ilu(A,options) は、構造体 options で指定されたオプションを使用して、A の不完全 LU 分解を実行します。

たとえば、options の type フィールドを "ilutp" に設定して、ピボットなしの不完全 LU 分解を実行できます。その後、milu フィールドを "row" または "col" に設定して、行の和または列の和を保持する変更された不完全 LU 分解を指定できます。オプションをこのように組み合わせると、"row" オプション (U が列置換される) の場合は L と U が A*P の不完全因子となり、"col" オプション (L が行置換される) の場合は L と U が P*A の不完全因子となる置換行列 P が返されます。

例

さまざまなタイプの不完全 LU 分解

関数 ilu では、ゼロで埋める分解 (ILU(0))、Crout バージョン (ILUC)、棄却とピボットのしきい値をもつ分解 (ILUTP) の 3 種類の不完全 LU 分解を行います。

既定では、ilu はスパース行列入力のゼロで埋める不完全 LU 分解を実行します。たとえば、7840 個の非ゼロ要素をもつスパース行列の完全分解と不完全分解を求めるとします。その完全 LU 因子は 126,478 個の非ゼロ要素をもち、ゼロ埋め込みを使用するその不完全 LU 因子は、A と同じ数の 7840 個の非ゼロ要素をもちます。

A = gallery("neumann",1600) + speye(1600);
n = nnz(A)

n = 7840

n = nnz(lu(A))

n = 126478

n = nnz(ilu(A))

n = 7840

ゼロで埋める分解ではその LU 因子で入力行列のスパース パターンが保持されるため、分解の相対誤差は、A の非ゼロ要素のパターンでは基本的にゼロです。

[L,U] = ilu(A);
e = norm(A-(L*U).*spones(A),"fro")/norm(A,"fro")

e = 4.8874e-17

ただし、このようなゼロで埋められた因子の積は、元の行列を十分に近似していません。

e = norm(A-L*U,"fro")/norm(A,"fro")

e = 0.0601

精度を高めるには、非スパースを使う他のタイプの不完全 LU 分解を使用します。たとえば、棄却許容誤差が 1e-6 の Crout バージョンを使用します。

options.droptol = 1e-6;
options.type = "crout";
[L,U] = ilu(A,options);

Crout バージョンの不完全分解の LU 因子は 51,482 個の非ゼロ要素をもちます (完全分解より少ない)。非スパースを使用した不完全 LU 因子の積のほうが、元の行列を良く近似しています。

n = nnz(ilu(A,options))

n = 51482

e = norm(A-L*U,"fro")./norm(A,"fro")

e = 9.3040e-07

比較のために、同じ入力行列 A について棄却とピボットのしきい値をもつ不完全分解を行うと、Crout バージョンと同様の結果になります。

options.type = "ilutp";
[L,U,P] = ilu(A,options);
n = nnz(ilu(A,options))

n = 51541

norm(P*A-L*U,"fro")./norm(A,"fro")

ans = 9.4960e-07

不完全 LU 分解の棄却許容誤差

不完全 LU 分解の棄却許容誤差を変更してスパース行列を因数分解します。

行列 west0479 を読み込みます。これは 479 行 479 列の実数値の非対称スパース行列です。condest を使用して行列の条件数を推定します。

load west0479
A = west0479;
c1 = condest(A)

c1 = 1.4244e+12

equilibrateを使用して行列の条件数を改善します。元の行列 A を並べ替えて再スケーリングし、より良い条件数をもち、かつ対角要素が 1 と –1 のみの新しい行列 B = R*P*A*C を作成します。

[P,R,C] = equilibrate(A);
B = R*P*A*C;
c2 = condest(B)

c2 = 5.1036e+04

棄却とピボットのしきい値をもち、行の和を保持する B の不完全 LU 分解を実行するようにオプションを指定します。比較のために、まず、非スパースの棄却許容誤差としてゼロを指定して、完全な LU 分解を行います。

options.type = "ilutp";
options.milu = "row";
options.droptol = 0;
[L,U,P] = ilu(B,options);

この因数分解では、入力行列 B の近似の精度が非常に高くなりますが、因子は B より大幅に密になります。

e = norm(B*P-L*U,"fro")/norm(B,"fro")

e = 1.0345e-16

nLU = nnz(L)+nnz(U)-size(B,1)

nLU = 19118

nB = nnz(B)

nB = 1887

棄却許容誤差を変更して、スパース性を上げて B の近似の精度を下げた不完全 LU 因子を取得できます。たとえば、以下のプロットは、棄却許容誤差に対してプロットした入力行列の密度に対する不完全因子の密度の割合と、不完全分解の相対誤差を示します。

ntols = 20;
tau = logspace(-6,-2,ntols);
e = zeros(1,ntols);
nLU = zeros(1,ntols);
for k = 1:ntols
    options.droptol = tau(k);
    [L,U,P] = ilu(B,options);
    nLU(k) = nnz(L)+nnz(U)-size(B,1);
    e(k) = norm(B*P-L*U,"fro")/norm(B,"fro");
end
figure
semilogx(tau,nLU./nB,LineWidth=2)
title("Ratio of nonzeros of LU factors with respect to B")
xlabel("drop tolerance")
ylabel("nnz(L)+nnz(U)-size(B,1)/nnz(B)",FontName="FixedWidth")

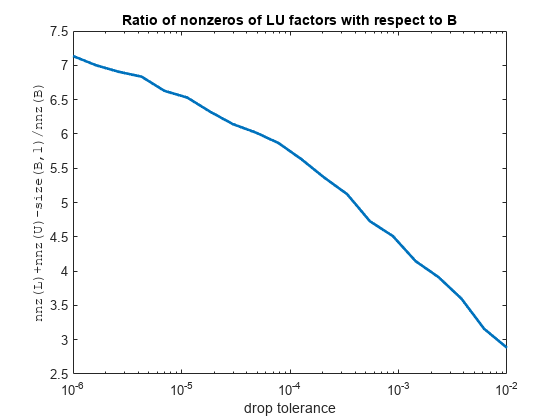
figure
loglog(tau,e,LineWidth=2)
title("Relative error of the incomplete LU factorization")
xlabel("drop tolerance")
ylabel("$||BP-LU||_F\,/\,||B||_F$",Interpreter="latex")

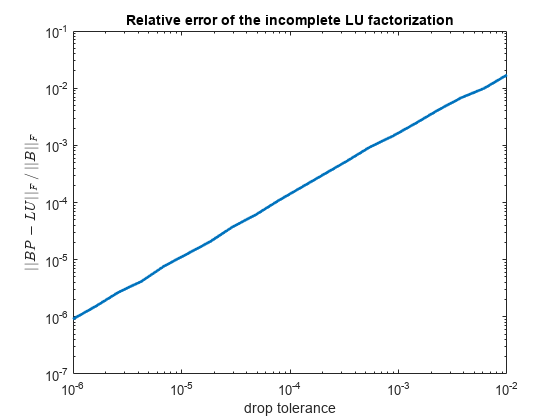
この例では、しきい値棄却による不完全 LU 分解の相対誤差は、棄却許容誤差と同じ次元にあります (常に同じとは限りません)。

ilu を前処理行列として使用した線形システムの求解

不完全 LU 分解をbicgstabの前処理行列として使用して線形システムを解きます。

479 行 479 列の非対称実スパース行列 west0479 を読み込みます。

load west0479
A = west0479;

$\mathit{Ax}=\mathit{b}$ に対する真の解がすべて 1 のベクトルになるように、b を定義します。

b = full(sum(A,2));

許容誤差と最大反復回数を設定します。

tol = 1e-12;
maxit = 20;

bicgstab を使用して、要求された許容誤差と反復回数で解を求めます。解法プロセスに関する情報を返す出力を 5 つ指定します。

• x は A*x = b の計算された解です。

• fl0 はアルゴリズムが収束したかどうかを示すフラグです。

• rr0 は計算解 x の相対残差です。

• it0 は x が計算されたときの反復回数です。

• rv0 は半分の反復ごとに得られる $\Vert \mathit{b}-\mathit{Ax}\Vert$ の残差履歴のベクトルです。

[x,fl0,rr0,it0,rv0] = bicgstab(A,b,tol,maxit); 
fl0

fl0 = 1

rr0

rr0 = 1

it0

it0 = 0

fl0 は、bicgstab が要求した反復回数 20 回以内に要求した許容誤差 1e-12 に収束しなかったため 1 となります。実際、bicgstab の動作が良好でないために初期推定 x0 = zeros(size(A,2),1) が最適解であり、it0 = 0 で示されるとおり、これが返されます。

遅い収束への対応として、前処理行列を指定できます。A は非対称であるため、ilu を使用して前処理行列 $\mathit{M}=\mathit{L}\mathit{U}$ を生成します。棄却許容誤差を指定して、1e-6 よりも小さい値をもつ非対角エントリを無視します。bicgstab への入力として L および U を指定して、前処理された系 ${\mathit{A}\mathit{M}}^{-1}\mathit{M}\mathit{x}=\mathit{b}$ を解きます。

options = struct("type","ilutp","droptol",1e-6);
[L,U] = ilu(A,options);
[x_precond,fl1,rr1,it1,rv1] = bicgstab(A,b,tol,maxit,L,U);
fl1

fl1 = 0

rr1

rr1 = 7.0681e-14

it1

it1 = 3

ilu 前処理行列を使用すると、3 回目の反復で 1e-12 の要求された許容誤差より少ない相対残差 rr1 が生成されます。出力 rv1(1) は norm(b)、出力 rv1(end) は norm(b-A*x1) になります。

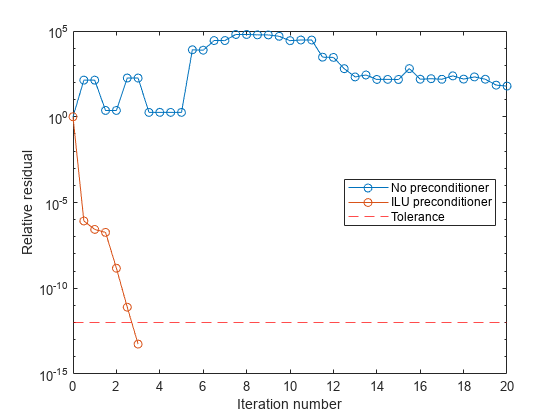
半分の反復ごとでの相対残差をプロットして、bicgstab の進行状況を確認できます。指定された許容誤差のラインと共に、それぞれの解の残差履歴をプロットします。

semilogy((0:numel(rv0)-1)/2,rv0/norm(b),"-o")
hold on
semilogy((0:numel(rv1)-1)/2,rv1/norm(b),"-o")
yline(tol,"r--");
legend("No preconditioner","ILU preconditioner","Tolerance",Location="East")
xlabel("Iteration number")
ylabel("Relative residual")

入力引数

A — 入力行列

スパース正方行列

入力行列。スパース正方行列として指定します。

options — LU 分解オプション

構造体

LU 分解オプション。最大 5 つのフィールドをもつ構造体として指定します。

フィールド名	まとめ	説明
type	不完全 LU 分解のタイプ	type の有効な値は次のとおりです。 "nofill"(既定) — ILU(0) としても知られる、0 レベルの要素を満たす ILU 分解を実行します。type が "nofill" に設定されている場合、milu オプションのみが使用されます。すべての他のフィールドは無視されます。 "crout" — Crout バージョンの ILU 分解 (ILUC と呼ばれる) を実行します。type が "crout" に設定されている場合、droptol オプションと milu オプションのみが使用され、その他すべてのフィールドは無視されます。 "ilutp" — しきい値とピボットを使用した ILU 分解 (ILUTP と呼ばれる) を実行します。ピボットはこのタイプでのみ実行されます。 既定値は "nofill" です。
droptol	不完全 LU 分解の棄却許容誤差	droptol の有効な値は任意の非負のスカラーです。U の非ゼロ要素は、abs(U(i,j)) >= droptol*norm(A(:,j)) を満たします。ただし、対角要素は例外で、これは、この条件を満たすかどうかに関係なく保持されます。L の要素は、ピボットによってスケーリングされる前にローカルな棄却許容誤差に対してテストされるので、L の非ゼロ要素は abs(L(i,j)) >= droptol*norm(A(:,j))/U(j,j) を満たします。 既定値は 0 で、完全な LU 分解を行います。
milu	変更された不完全 LU 分解のタイプ	milu の有効な値は次のとおりです。 "off" — 変更された不完全 LU 分解は行われません。 "row" — 行和で変更された不完全 LU 分解を行います。上三角因子 U の対角要素は、元の行列の行和を保持するように補正されます。つまり、A*e = L*U*e になります。ここで、e は 1 の列ベクトルです。 "col" — 列和で変更された不完全 LU 分解を行います。上三角因子 U の対角要素は、元の行列の列和を保持するように補正されます。つまり、e'*A = e'*L*U です。 既定値は "off" です。
udiag	U のゼロの対角要素を置き換えるかどうか	udiag の有効な値は 0 および 1 です。udiag が 1 の場合、上三角因子 U のゼロの対角要素は、特異因子を避けるために、ローカルな棄却許容誤差に置き換えられます。 既定値は 0 です。
thresh	ピボットしきい値	有効な値は、0 (アルゴリズムによって対角ピボットが選択される) から 1 (アルゴリズムによって列の最大要素がピボットに選択される) の間の値です。ピボット操作は、ある列の対角要素の大きさが、その列内の 1 つ下の対角要素の thresh 倍よりも小さい場合に生じます。 既定値は 1 です。

出力引数

L — 下三角因子

スパース正方行列

下三角因子。スパース正方行列として返されます。

• options.type として "nofill" (既定値) または "crout" を指定した場合、L は単位下三角行列 (つまり、主対角が 1 の下三角行列) として返されます。

• options.type として "ilutp" を指定し、options.milu として "col" を指定した場合、L は行置換された単位下三角行列として返されます。

U — 上三角因子

スパース正方行列

上三角因子。スパース正方行列として返されます。

• options.type として "nofill" (既定値) または "crout" を指定した場合、U は上三角行列として返されます。

• options.type として "ilutp" を指定し、options.milu として "row" を指定した場合、U は列置換された上三角行列として返されます。

P — 置換行列

スパース正方行列

置換行列。スパース正方行列として返されます。

options.type として "nofill" (既定値) または "crout" を指定した場合、どちらのタイプもピボットを実行しないため、P は A と同じサイズの単位行列として返されます。

W — LU 因子の非ゼロ要素

スパース正方行列

LU 因子の非ゼロ要素。スパース正方行列として返されます。ここで、W = L + U - speye(size(A)) です。

ヒント

• この関数で返される不完全分解は、bicg、bicgstab、gmres など、反復メソッドで解かれる線形方程式系の前処理行列として使用できることがあります。

参照

[1] Saad, Y. "Preconditioning Techniques", chap. 10 in Iterative Methods for Sparse Linear Systems. The PWS Series in Computer Science. Boston: PWS Pub. Co, 1996.

拡張機能

スレッドベースの環境

MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。

この関数はスレッドベースの環境を完全にサポートしています。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。

分散配列

Parallel Computing Toolbox™ を使用して、クラスターの結合メモリ上で大きなアレイを分割します。

使用上の注意事項および制限事項:

• type フィールドを構造体配列 options に含めている場合、それを 'nofill' に設定しなければなりません。

詳細については、分散配列を使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2007a で導入

参考

lu | ichol | bicg | bicgstab | gmres

トピック

• スパース行列の演算
• 線形方程式の反復法

×

例を開く

この例の変更されたバージョンがあります。編集された方の例を開きますか?

いいえ、変更されたバージョンを上書きします。 はい