equilibrate

条件を改善するための行列のスケーリング

構文

[P,R,C] = equilibrate(A)

[P,R,C] = equilibrate(A,outputForm)

説明

[P,R,C] = equilibrate(A) は、新しい行列 B = R*P*A*C の対角要素が大きさ 1 であり、非対角要素の大きさが 1 未満になるように、行列 A を並べ替えて再スケーリングします。

[P,R,C] = equilibrate(A,outputForm) は、outputForm で指定した形式で出力 P、R、および C を返します。たとえば、outputForm を "vector" に指定すると、出力を列ベクトルとして返すことができます。

例

条件を改善するために行列を平衡化

大きな条件数をもつ行列を平衡化して、反復ソルバー gmres による線形系の解の効率と安定性を改善します。

行列 west0479 を読み込みます。これは 479 行 479 列の実数値のスパース行列です。condest を使用して、行列の推定条件数を計算します。

load west0479
A = west0479;
c1 = condest(A)

c1 = 1.4244e+12

反復 450 回、許容誤差 1e-11 を指定して gmres を使用し、線形系 $\mathrm{Ax}=\mathit{b}$ を解いてみます。gmres が反復ごとに解の残差ノルムを返すように、5 つの出力を指定します (~ を使用して不要な出力を抑制)。残差ノルムを片対数プロットでプロットします。このプロットは、gmres が妥当な残差ノルムに到達できず、$\mathit{x}$ について計算された解が信頼できないことを示します。

b = ones(size(A,1),1);
tol = 1e-11;
maxit = 450;
[x,flx,~,~,rvx] = gmres(A,b,[],tol,maxit);
semilogy(rvx)
title('Residual Norm at Each Iteration')

equilibrate を使用して、A の並べ替えと再スケーリングをします。より良い条件数をもち、かつ対角要素が 1 と -1 のみの新しい行列 B = R*P*A*C を作成します。

[P,R,C] = equilibrate(A);
B = R*P*A*C;
c2 = condest(B)

c2 = 5.1036e+04

equilibrate により返された出力を使用して、問題 $\mathrm{Ax}=\mathit{b}$ を式 $\mathrm{By}=\mathit{d}$ に書き換えることができます。ここで、$\mathit{B}=\mathrm{RPAC}$、$\mathit{d}=\mathrm{RPb}$ です。この形式では、元の系の解を $\mathit{x}=\mathrm{Cy}$ で復元できます。ただし、復元された解は、元の系の望ましい残差誤差をもたない可能性があります。詳細については、再スケーリングによる線形系の求解を参照してください。

gmres を使用して $\mathrm{By}=\mathit{d}$ を $\mathit{y}$ について解き、反復ごとの残差ノルムを再プロットします。このプロットは、行列の平衡化によって問題の安定性が高まり、gmres が反復 200 回未満で目的の許容誤差 1e-11 に収束することを示します。

d = R*P*b;
[y,fly,~,~,rvy] = gmres(B,d,[],tol,maxit);
hold on
semilogy(rvy)
legend('Original', 'Equilibrated', 'Location', 'southeast')
title('Relative Residual Norms (No Preconditioner)')
hold off

前処理行列を使用した解の改善

行列 B を得た後に、gmres と共に使用する前処理行列を計算して、さらに問題の安定性を改善することができます。B の数値特性は元の行列 A の数値特性よりも優れているため、平衡化した行列を使用して前処理行列を計算することが望まれます。

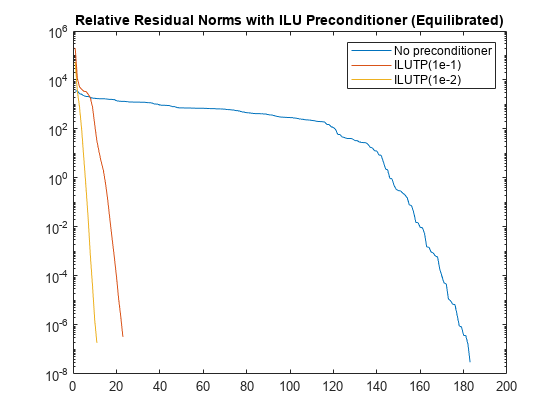
ilu を使用して 2 つの異なる前処理行列を計算し、それらを gmres の入力として使用して問題を再び解きます。比較のために、平衡化したノルムと同じプロットに反復ごとの残差ノルムをプロットします。このプロットは、平衡化した行列を使用した前処理行列の計算によって問題の安定性が大幅に高まり、gmres が反復 30 回未満で目的の許容誤差に達することを示します。

semilogy(rvy)
hold on

[L1,U1] = ilu(B,struct('type','ilutp','droptol',1e-1,'thresh',0));
[yp1,flyp1,~,~,rvyp1] = gmres(B,d,[],tol,maxit,L1,U1);
semilogy(rvyp1)

[L2,U2] = ilu(B,struct('type','ilutp','droptol',1e-2,'thresh',0));
[yp2,flyp2,~,~,rvyp2] = gmres(B,d,[],tol,maxit,L2,U2);
semilogy(rvyp2)

legend('No preconditioner', 'ILUTP(1e-1)', 'ILUTP(1e-2)')
title('Relative Residual Norms with ILU Preconditioner (Equilibrated)')
hold off

出力形式の指定

6 行 6 列の魔方陣行列を作成し、equilibrate を使用して行列を因数分解します。既定では、equilibrate は置換情報およびスケーリング係数を行列として返します。

A = magic(6)

A = 6×6

    35     1     6    26    19    24
     3    32     7    21    23    25
    31     9     2    22    27    20
     8    28    33    17    10    15
    30     5    34    12    14    16
     4    36    29    13    18    11

[P,R,C] = equilibrate(A)

P = 6×6

     0     0     0     0     1     0
     0     0     0     0     0     1
     0     0     0     1     0     0
     1     0     0     0     0     0
     0     0     1     0     0     0
     0     1     0     0     0     0

R = 6×6

    0.1852         0         0         0         0         0
         0    0.1749         0         0         0         0
         0         0    0.1909         0         0         0
         0         0         0    0.1588         0         0
         0         0         0         0    0.1793         0
         0         0         0         0         0    0.1966

C = 6×6

    0.1799         0         0         0         0         0
         0    0.1588         0         0         0         0
         0         0    0.1588         0         0         0
         0         0         0    0.2422         0         0
         0         0         0         0    0.2066         0
         0         0         0         0         0    0.2035

行列の因子 P、R、および C を使用して平衡行列 Bmatrix を作成します。

Bmatrix = R*P*A*C

Bmatrix = 6×6

    1.0000    0.1471    1.0000    0.5385    0.5358    0.6031
    0.1259    1.0000    0.8056    0.5509    0.6506    0.3916
    0.2747    0.8485    1.0000    0.7859    0.3943    0.5825
    1.0000    0.0252    0.1513    1.0000    0.6233    0.7754
    1.0000    0.2562    0.0569    0.9553    1.0000    0.7295
    0.1061    0.9988    0.2185    1.0000    0.9341    1.0000

次に、"vector" オプションを指定して出力をベクトルとして返します。入力行列が大きい場合、出力をベクトルとして返すとメモリ消費量が少なくなり、効率性が向上します。

[p,r,c] = equilibrate(A,"vector")

p = 6×1

     5
     6
     4
     1
     3
     2

r = 6×1

    0.1852
    0.1749
    0.1909
    0.1588
    0.1793
    0.1966

c = 6×1

    0.1799
    0.1588
    0.1588
    0.2422
    0.2066
    0.2035

ベクトル出力 p、r、および c を使用して平衡行列 Bvector を作成します。

Bvector = r.*A(p,:).*c'

Bvector = 6×6

    1.0000    0.1471    1.0000    0.5385    0.5358    0.6031
    0.1259    1.0000    0.8056    0.5509    0.6506    0.3916
    0.2747    0.8485    1.0000    0.7859    0.3943    0.5825
    1.0000    0.0252    0.1513    1.0000    0.6233    0.7754
    1.0000    0.2562    0.0569    0.9553    1.0000    0.7295
    0.1061    0.9988    0.2185    1.0000    0.9341    1.0000

Bvector と Bmatrix を比較します。結果で等しいことが示されます。

norm(Bmatrix - Bvector)

ans = 0

入力引数

A — 入力行列

正方行列

入力行列。正方行列として指定します。A は密でもスパースでも構いませんが、sprank の判定で構造的に非特異でなければなりません。

A がスパースである場合、出力 P、R、および C もスパースになります。

データ型: single | double
複素数のサポート: あり

outputForm — 出力形式

"matrix" (既定値) | "vector"

出力形式。"vector" または "matrix" として指定します。このオプションにより、出力 P、R、および C を列ベクトルとして返すのか行列として返すのかを指定できます。

• "matrix" — P、R、および C は B = R*P*A*C を満たす行列になります。

• "vector" — P、R、および C は B = R.*A(P,:).*C' を満たす列ベクトルになります。

例: [P,R,C] = equilibrate(A,"vector") では、P、R、および C がベクトルとして返されます。

出力引数

P — 置換情報

行列 (既定値) | ベクトル

置換情報。行列またはベクトルとして返されます。P*A (または "vector" オプションの場合は A(P,:)) は、対角要素の積の絶対値が最大になるように A を並べ替えたものです。

R — 行のスケーリング

対角行列 (既定値) | ベクトル

行のスケーリング。対角行列またはベクトルとして返されます。R と C の非ゼロのエントリは正の実数です。

C — 列のスケーリング

対角行列 (既定値) | ベクトル

列のスケーリング。対角行列またはベクトルとして返されます。R と C の非ゼロのエントリは正の実数です。

詳細

再スケーリングによる線形系の求解

線形系の解 x = A\b では、A の条件数が計算の精度と効率性のために重要になります。equilibrate では、基底ベクトルを再スケーリングすることで A の条件数を改善させることができます。これによって、b と x の両方を表現できる新しい座標系が効果的に形成されます。

equilibrate は、元の系 x = A\b のベクトル b および x のスケールが無関係である場合に最も役立ちます。ただし、b と x のスケールが関連 "している" 場合は、equilibrate を使用して、線形系の求解に対して A のみを再スケーリングすることはお勧めできません。得られた解では通常、元の基底ベクトルを使用して表された場合でも、元の系の小さい残差が得られません。

参照

[1] Duff, I. S., and J. Koster. “On Algorithms For Permuting Large Entries to the Diagonal of a Sparse Matrix.” SIAM Journal on Matrix Analysis and Applications 22, no. 4 (January 2001): 973–96.

拡張機能

スレッドベースの環境

MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。

この関数はスレッドベースの環境を完全にサポートしています。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。

バージョン履歴

R2019a で導入

R2022a: 出力形式の指定

outputForm を "vector" または "matrix" に指定することで、equilibrate が出力引数をベクトルと行列のどちらとして返すかを制御します。因数分解が大規模な場合、出力をベクトルとして返すとメモリ消費量が少なくなり、効率性が向上します。

参考

matchpairs | sprank | ilu | ichol | balance | gmres