eigs

固有値および固有ベクトルのサブセット

構文

d = eigs(A)

d = eigs(A,k)

d = eigs(A,k,sigma)

d = eigs(A,k,sigma,Name,Value)

d = eigs(A,k,sigma,opts)

d = eigs(A,B,___)

d = eigs(Afun,n,___)

[V,D] = eigs(___)

[V,D,flag] = eigs(___)

説明

d = eigs(A) は、行列 A について、絶対値が最も大きい 6 個の固有値からなるベクトルを返します。これは大規模なスパース行列など、eig を使用してすべての固有値を計算すると計算負荷が高くなる場合に非常に便利です。

d = eigs(A,k) は、絶対値が最も大きい k 個の固有値を返します。

d = eigs(A,k,sigma) は sigma の値に基づいて、k 個の固有値を返します。たとえば、eigs(A,k,'smallestabs') は絶対値が最も小さい k 個の固有値を返します。

d = eigs(A,k,sigma,Name,Value) は、1 つ以上の名前と値のペアの引数を使用して追加オプションを指定します。たとえば、eigs(A,k,sigma,'Tolerance',1e-3) はアルゴリズムの収束の許容誤差を調整します。

d = eigs(A,k,sigma,opts) は構造体を使用してオプションを指定します。

d = eigs(A,B,___) は一般化固有値問題 A*V = B*V*D を求解します。オプションで、k、sigma、opts または名前と値のペアの引数を追加の入力引数として指定できます。

d = eigs(Afun,n,___) は、行列ではなく関数ハンドル Afun を指定します。2 番目の入力 n は、Afun で使用される行列 A のサイズを指定します。オプションで、B、k、sigma、opts または名前と値のペアの引数を追加の入力引数として指定できます。

[V,D] = eigs(___) は、主対角に固有値を含む対角行列 D と、対応する固有ベクトルを列に含む行列 V を返します。前述の構文にある任意の入力引数の組み合わせが使用できます。

[V,D,flag] = eigs(___) は、収束フラグも返します。flag が 0 の場合、すべての固有値は収束しています。

例

スパース行列の最大の固有値

行列 A = delsq(numgrid('C',15)) は、区間 (0 8) にほど良く配置された固有値をもつ対称正定値行列です。絶対値が最も大きい 6 個の固有値を計算します。

A = delsq(numgrid('C',15));
d = eigs(A)

d = 6×1

    7.8666
    7.7324
    7.6531
    7.5213
    7.4480
    7.3517

2 番目の入力を指定して、最も大きい特定数の固有値を計算します。

d = eigs(A,3)

d = 3×1

    7.8666
    7.7324
    7.6531

スパース行列の最小の固有値

行列 A = delsq(numgrid('C',15)) は、区間 (0 8) にほど良く配置された固有値をもつ対称正定値行列です。最も小さい 5 個の固有値を計算します。

A = delsq(numgrid('C',15));  
d = eigs(A,5,'smallestabs')

d = 5×1

    0.1334
    0.2676
    0.3469
    0.4787
    0.5520

関数ハンドルを使用した固有値

非ゼロ要素の密度が約 25% の、1500 行 1500 列の乱数スパース行列を作成します。

n = 1500;
A = sprand(n,n,0.25);

行列の LU 分解を求め、A(p,:) = L*U を満たす置換ベクトル p を返します。

[L,U,p] = lu(A,'vector');

関数ハンドル Afun を作成します。この関数ハンドルはベクトル入力 x を受け取り、LU 分解の結果を使用して、実質的に A\x を返します。

Afun = @(x) U\(L\(x(p)));

eigs と関数ハンドル Afun を使用して、絶対値の最も小さい 6 個の固有値を計算します。2 番目の入力は A のサイズです。

d = eigs(Afun,1500,6,'smallestabs')

d = 6×1 complex

   0.1423 + 0.0000i
   0.4859 + 0.0000i
  -0.3323 - 0.3881i
  -0.3323 + 0.3881i
   0.1019 - 0.5381i
   0.1019 + 0.5381i

固有値のタイプ

west0479 は 479 行 479 列の実数値スパース行列であり、共役固有値の実数および複素数のペアをもちます。

west0479 行列を読み込み、eig を使用してすべての固有値を計算してプロットします。固有値は複素数であるため、plot は自動的に実数部を x 座標、虚数部を y 座標として使用します。

load west0479
A = west0479;
d = eig(full(A));
plot(d,'+')

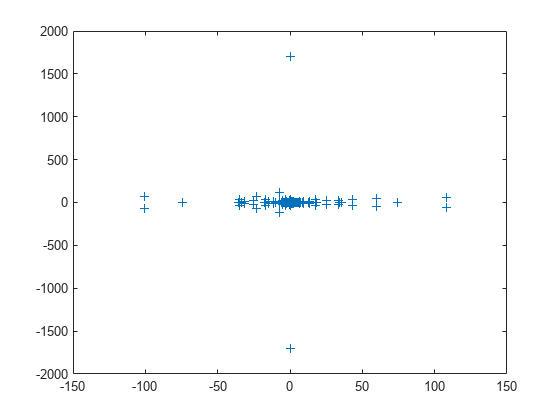
固有値は、実数直線 (x 軸) に沿って、特に原点近くに集まっています。

eigs には、各種の最大の固有値または最小の固有値を取り出すことができる sigma のオプションがいくつかあります。sigma で使用できるオプションごとに、いくつかの固有値を計算してプロットします。

figure
plot(d, '+')
hold on
la = eigs(A,6,'largestabs');
plot(la,'ro')
sa = eigs(A,6,'smallestabs');
plot(sa,'go')
hold off
legend('All eigenvalues','Largest magnitude','Smallest magnitude')
xlabel('Real axis')
ylabel('Imaginary axis')

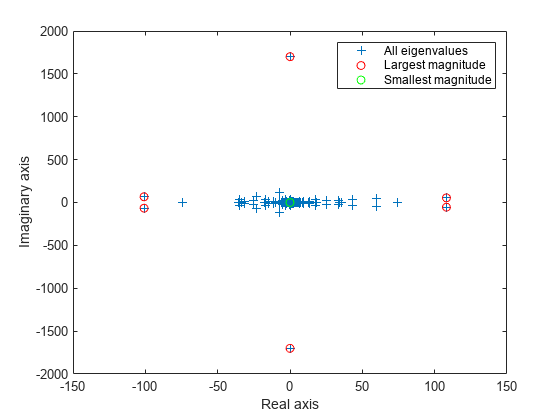
figure
plot(d, '+')
hold on
ber = eigs(A,4,'bothendsreal');
plot(ber,'r^')
bei = eigs(A,4,'bothendsimag');
plot(bei,'g^')
hold off
legend('All eigenvalues','Both ends real','Both ends imaginary')
xlabel('Real axis')
ylabel('Imaginary axis')

figure
plot(d, '+')
hold on
lr = eigs(A,3,'largestreal');
plot(lr,'ro')
sr = eigs(A,3,'smallestreal');
plot(sr,'go')
li = eigs(A,3,'largestimag','SubspaceDimension',45);
plot(li,'m^')
si = eigs(A,3,'smallestimag','SubspaceDimension',45);
plot(si,'c^')
hold off
legend('All eigenvalues','Largest real','Smallest real','Largest imaginary','Smallest imaginary')
xlabel('Real axis')
ylabel('Imaginary axis')

'smallestabs' の固有値と 'smallestreal' の固有値の違い

対称正定値スパース行列を作成します。

A = delsq(numgrid('C', 150));

'smallestreal' を使用して、最も小さい 6 個の実数固有値を計算します。この場合、A を使用して Krylov 法が実行されます。

tic
d = eigs(A, 6, 'smallestreal')

d = 6×1

    0.0013
    0.0025
    0.0033
    0.0045
    0.0052
    0.0063

toc

Elapsed time is 3.546209 seconds.

'smallestabs' を使用して、同じ固有値を計算します。この場合、A の逆行列を使用して Krylov 法が実行されます。

tic
dsm = eigs(A, 6, 'smallestabs')

dsm = 6×1

    0.0013
    0.0025
    0.0033
    0.0045
    0.0052
    0.0063

toc

Elapsed time is 0.475066 seconds.

固有値はゼロの近くに集まります。A を使用する 'smallestreal' の計算は収束に時間がかかります。これは、固有値間のギャップが非常に小さいためです。反対に、'smallestabs' オプションでは A の逆行列を使用するため、A の固有値の逆行列でギャップがはるかに大きくなり、結果として計算が容易になります。このパフォーマンスの改善は、'smallestreal' では不要な A の因子分解を行うことで得られます。

固有値近傍の sigma 値

固有値とほぼ等しい数値 sigma の近傍の固有値を計算します。

行列 A = delsq(numgrid('C',30)) は、区間 (0 8) にほど良く配置された固有値をもつサイズ 632 の対称正定値行列です。ただし、このうちの 18 個の固有値は、4.0 の位置で反復があります。4.0 近傍の固有値をいくつか計算するには、関数呼び出し eigs(A,20,4.0) を試みるのが妥当です。ただし、この呼び出しは A - 4.0*I の逆行列の最大固有値を計算します。ここで、I は単位行列です。4.0 は A の固有値であるため、この行列は特異であり、逆行列はありません。eigs は失敗してエラー メッセージが出力されます。数値 sigma は、固有値と厳密に等しい値にできません。これらの固有値を求めるには、代わりに 4.0 近傍 (等しくない) の sigma 値を使用しなければなりません。

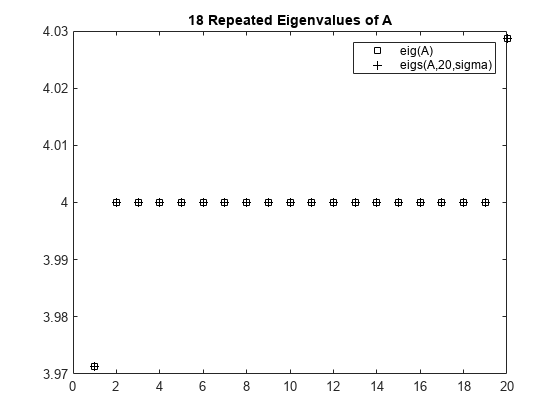
eig を使用してすべての固有値を計算し、eigs を使用して 4 - 1e-6 に最も近い 20 個の固有値を求めて、それらの結果を比較します。それぞれの方法で計算した固有値をプロットします。

A = delsq(numgrid('C',30)); 
sigma = 4 - 1e-6;
d = eig(A);
D = sort(eigs(A,20,sigma));

plot(d(307:326),'ks')
hold on
plot(D,'k+')
hold off
legend('eig(A)','eigs(A,20,sigma)') 
title('18 Repeated Eigenvalues of A')

置換されたコレスキー因子の固有値

どちらも非ゼロ要素の密度の低い、乱数のスパース行列 A および B を作成します。

B = sprandn(1e3,1e3,0.001) + speye(1e3); 
B = B'*B; 
A = sprandn(1e3,1e3,0.005); 
A = A+A';

行列 B のコレスキー分解を求め、3 つの出力を使用して置換ベクトル s およびテスト値 p を返します。

[R,p,s] = chol(B,'vector');
p

p = 
0

p はゼロであるため、B は B(s,s) = R'*R を満たす対称正定値行列です。

A および R に関する一般化固有値問題について、絶対値が最も大きい 6 個の固有値および固有ベクトルを計算します。R は B のコレスキー因子であるため、'IsCholesky' を true として指定します。さらに、B(s,s) = R'*R であり、したがって R = chol(B(s,s)) であるため、置換ベクトル s を 'CholeskyPermutation' の値として使用します。

[V,D,flag] = eigs(A,R,6,'largestabs','IsCholesky',true,'CholeskyPermutation',s);
flag

flag = 
0

flag はゼロであるため、すべての固有値が収束しています。

入力引数

A — 入力行列

行列

入力行列。正方行列として指定します。A は通常 (必ずではない)、大きなスパース行列です。

A が対称である場合、eigs はそうした場合専用のアルゴリズムを使用します。A が "ほぼ" 対称である場合は、A = (A+A')/2 を使用して A を対称にしてから eigs を呼び出すことを検討してください。これにより、eigs は複素数固有値ではなく、実数固有値を確実に計算します。

データ型: single | double
複素数のサポート: あり

B — 入力行列

行列

入力行列。A と同じサイズの正方行列として指定します。B が指定された場合、eigs は一般化固有値問題 A*V = B*V*D を求解します。

B が対称正定値である場合、eigs はそうした場合専用のアルゴリズムを使用します。B が "ほぼ" 対称正定値である場合は、B = (B+B')/2 を使用して B を対称にしてから eigs を呼び出すことを検討してください。

A がスカラーの場合、B を空行列 eigs(A,[],k) として指定して標準固有値問題を解くことで、B と k のあいまいさを解決できます。

データ型: single | double
複素数のサポート: あり

k — 計算する固有値の数

スカラー

計算する固有値の数。正のスカラー整数として指定します。k が size(A,2) よりも大きい場合、eigs は有効な最大値である k = size(A,2) を代わりに使用します。

例: eigs(A,2) は A の最も大きい固有値を 2 つ返します。

sigma — 固有値のタイプ

'largestabs' (既定値) | 'smallestabs' | 'largestreal' | 'smallestreal' | 'bothendsreal' | 'largestimag' | 'smallestimag' | 'bothendsimag' | スカラー

固有値のタイプ。次の表のいずれかの値として指定します。

sigma	説明	sigma (R2017a 以前)
scalar (0 を含む実数、複素数)	数値 sigma に最も近い固有値。	変更なし
'largestabs' (既定)	最大の絶対値。	'lm'
'smallestabs'	最小固有値。sigma = 0 と同じ。	'sm'
'largestreal'	最大の実数値。	'lr', 'la'
'smallestreal'	最小の実数値。	'sr', 'sa'
'bothendsreal'	それぞれ最大の実数部および最小の実数部をもつ、両端の k/2 個の値 (k が奇数の場合、大きいほうの端を 1 つ余分にとる)。	'be'

非対称問題では、sigma は次の値にすることもできます。

sigma	説明	sigma (R2017a 以前)
'largestimag'	最大虚数部。	A が複素数の場合、'li'。
'smallestimag'	最小虚数部。	A が複素数の場合、'si'。
'bothendsimag'	それぞれ最大の虚数部および最小の虚数部をもつ、両端の k/2 個の値 (k が奇数の場合、大きいほうの端を 1 つ余分にとる)。	A が実数の場合、'li'。

例: eigs(A,k,1) は 1 に最も近い k 個の固有値を返します。

例: eigs(A,k,'smallestabs') は絶対値が最も小さい k 個の固有値を返します。

データ型: single | double | char | string

opts — オプション構造体

構造体

オプション構造体。次の表の 1 つ以上のフィールドを含む構造体として指定します。

メモ

オプション構造体を使用したオプションの指定は推奨されません。代わりに名前と値のペアを使用してください。

オプション フィールド	説明	名前と値のペア
issym	Afun 行列の対称性。	'IsFunctionSymmetric'
tol	収束の許容誤差。	'Tolerance'
maxit	反復最大回数	'MaxIterations'
p	Lanczos 基底ベクトルの数。	'SubspaceDimension'
v0	開始ベクトル	'StartVector'
disp	診断情報の表示レベル。	'Display'
fail	収束していない固有値の出力での処理。	'FailureTreatment'
spdB	B は対称正定値か。	'IsSymmetricDefinite'
cholB	B はコレスキー因子 chol(B) か。	'IsCholesky'
permB	スパース行列 B が実際に chol(B(permB,permB)) である場合は、置換ベクトル permB を指定します。	'CholeskyPermutation'

例: opts.issym = 1, opts.tol = 1e-10 は、フィールド issym および tol に値が設定された構造体を作成します。

データ型: struct

Afun — 行列関数

関数ハンドル

行列関数。関数ハンドルとして指定します。関数 y = Afun(x) は、sigma の入力に応じて適切な値を返さなければなりません。

• A*x — sigma が未指定、または 'smallestabs' 以外のテキスト オプションの場合。

• A\x — sigma が 0 または 'smallestabs' の場合。

• (A-sigma*I)\x — sigma が非ゼロのスカラーである場合 (標準固有値問題)。

• (A-sigma*B)\x — sigma が非ゼロのスカラーである場合 (一般化固有値問題)。

たとえば、次の Afun は、sigma = 'smallestabs' を指定して eigs を呼び出すときに機能します。

[L,U,p] = lu(A,'vector');
Afun = @(x) U\(L\(x(p)));
d = eigs(Afun,100,6,'smallestabs')

一般化固有値問題の場合は、行列 B を次のように追加します (B は関数ハンドルで表すことができません)。

d = eigs(Afun,100,B,6,'smallestabs')

A は、'IsFunctionSymmetric' (または opts.issym) により対称であることが指定されている場合を除いて、非対称であると見なされます。'IsFunctionSymmetric' を true に設定すると、eigs は複素数固有値ではなく、実数固有値を確実に計算します。

関数 Afun に追加パラメーターを指定する方法の詳細については、関数のパラメーター化を参照してください。

ヒント

Afun から予測される出力を確認するには、'Display' オプションをオンにして eigs を呼び出します。

n — Afun で表される正方行列のサイズ

スカラー

Afun で表される正方行列 A のサイズ。正のスカラー整数として指定します。

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、コンマを使用して名前と値をそれぞれ区切り、Name を引用符で囲みます。

例: d = eigs(A,k,sigma,'Tolerance',1e-10,'MaxIterations',100) は収束の許容誤差を緩和し、より少ない反復回数を使用します。

一般オプション

Tolerance — 収束の許容誤差

1e-14 (既定値) | 正の実数のスカラー

収束の許容誤差。'Tolerance' と正の実数値スカラーで構成されるコンマ区切りのペアとして指定します。

例: s = eigs(A,k,sigma,'Tolerance',1e-3)

MaxIterations — アルゴリズムの最大反復回数

300 (既定値) | 正の整数

アルゴリズムの最大反復回数。'MaxIterations' と正の整数で構成されるコンマ区切りのペアとして指定します。

例: d = eigs(A,k,sigma,'MaxIterations',350)

SubspaceDimension — Krylov 部分空間の最大サイズ

max(2*k,20) (既定値) | 非負の整数

Krylov 部分空間の最大サイズ。'SubspaceDimension' と非負の整数で構成されるコンマ区切りのペアとして指定します。'SubspaceDimension' 値は、実対称問題の場合は k + 1 以上でなければならず、それ以外の場合は k + 2 です。ここで k は固有値の数です。

推奨値は p >= 2*k で、実非対称問題では p >= 2*k+1 です。'SubspaceDimension' 値が指定されない場合、既定のアルゴリズムにより、少なくとも 20 個の Lanczos ベクトルが使用されます。

eigs が収束しない問題では、'SubspaceDimension' の値を大きくすることで収束動作が改善される場合があります。ただし、値を大きくしすぎると、メモリの問題が発生することがあります。

例: d = eigs(A,k,sigma,'SubspaceDimension',25)

StartVector — 初期開始ベクトル

乱数ベクトル (既定値) | ベクトル

初期開始ベクトル。'StartVector' と数値ベクトルで構成されるコンマ区切りのペアとして指定します。

異なる乱数開始ベクトルを指定する主な理由は、ベクトルの生成に使用する乱数ストリームを制御するためです。

メモ

eigs は、プライベート乱数ストリームを使用する再現可能な方法で開始ベクトルを選択します。乱数のシードを変更しても、開始ベクトルには影響 "しません"。

例: d = eigs(A,k,sigma,'StartVector',randn(m,1)) は、グローバル乱数ストリームから値を取り出す乱数開始ベクトルを使用します。

データ型: single | double

FailureTreatment — 収束しない固有値の処理

'replacenan' (既定値) | 'keep' | 'drop'

収束しない固有値の処理。'FailureTreatment' と、'replacenan'、'keep'、'drop' のいずれかのオプションで構成されるコンマ区切りのペアとして指定します。

'FailureTreatment' の値は、eigs が収束しない固有値を出力に表示する方法を決定します。

オプション	出力への影響
'replacenan'	収束しない固有値を NaN 値に置き換えます。
'keep'	収束しない固有値を出力に含めます。
'drop'	収束しない固有値を出力から削除します。このオプションを使用すると、eigs は要求された数よりも少ない固有値を返す場合があります。

例: d = eigs(A,k,sigma,'FailureTreatment','drop') は収束していない固有値を出力から削除します。

データ型: char | string

Display — 診断情報の表示の切り替え

false または 0 (既定値) | true または 1

診断情報の表示の切り替え。'Display' と、数値または logical の 1 (true) または 0 (false) で構成されるコンマ区切りのペアとして指定します。計算中に診断情報の表示をオンにするには、値 true または 1 を指定します。

Afun のオプション

IsFunctionSymmetric — Afun 行列の対称性

true または 1 | false または 0

Afun 行列の対称性。'IsFunctionSymmetric' と、数値または logical の 1 (true) または 0 (false) で構成されるコンマ区切りのペアとして指定します。

このオプションは、Afun が入力ベクトルに適用する行列が対称であるかどうかを指定します。true または 1 の値を指定すると、eigs が対称行列に専用のアルゴリズムを使用して、実数固有値を返さなければならないことを示します。

一般化固有値問題 A*V = B*V*D 用のオプション

IsCholesky — B のコレスキー分解の切り替え

true または 1 | false または 0

B のコレスキー分解の切り替え。'IsCholesky' と、数値または logical の 1 (true) または 0 (false) で構成されるコンマ区切りのペアとして指定します。

このオプションは、呼び出し eigs(A,B,___) 内の行列 B の入力が R = chol(B) で実際に生成されたコレスキー因子 R であるかどうかを指定します。

メモ

sigma が 'smallestabs' または数値スカラーの場合は、このオプションを使用しないでください。

CholeskyPermutation — コレスキー置換ベクトル

1:n (既定値) | ベクトル

コレスキー置換ベクトル。'CholeskyPermutation' と数値ベクトルで構成されるコンマ区切りのペアとして指定します。スパース行列 B を chol(B(permB,permB)) に従って因子分解前に並べ替える場合は、置換ベクトル permB を指定します。

また、スパース行列の chol の 3 出力の構文を使用して、[R,p,permB] = chol(B,'vector') で permB を直接得ることもできます。

メモ

sigma が 'smallestabs' または数値スカラーの場合は、このオプションを使用しないでください。

IsSymmetricDefinite — B の対称正定性の切り替え

true または 1 | false または 0

B の対称正定性の切り替え。'IsSymmetricDefinite' と、数値または logical の 1 (true) または 0 (false) で構成されるコンマ区切りのペアとして指定します。B が対称正定値である、つまり、厳密に正の固有値をもつ対称行列だとわかっている場合は、true または 1 を指定します。

B が対称半正定値 (一部の固有値がゼロ) の場合に、'IsSymmetricDefinite' を true または 1 に指定すると、eigs は強制的に、B が対称正定値である場合に使用するものと同じ専用のアルゴリズムを使用します。

メモ

このオプションを使用するには、sigma の値が数値または 'smallestabs' でなければなりません。

出力引数

d — 固有値

列ベクトル

固有値。列ベクトルとして返されます。d は sigma の値によって異なる方法で並べ替えられます。

sigma の値	出力の並べ替え
'largestabs'	絶対値の降順
'largestreal'	実数部の降順
'largestimag'	虚数部の降順
'smallestabs'	絶対値の昇順
'smallestreal' 'bothendsreal'	実数部の昇順
'smallestimag'	虚数部の昇順
'bothendsimag'	虚数部の絶対値の降順

V — 固有ベクトル

行列

固有ベクトル。行列として返されます。V の列は、D の対角上の固有値に対応します。V の形式と正規化は、入力引数の組み合わせによって異なります。

• [V,D] = eigs(A) は、A*V = V*D となるような、A の右固有ベクトルを列にもつ行列 V を返します。V の固有ベクトルは、個々の 2 ノルムが 1 となるように正規化されます。

  A が対称の場合、固有ベクトル V は正規直交です。

• [V,D] = eigs(A,B) は、A*V = B*V*D を満たす一般化右固有ベクトルを列にもつ行列として V を返します。各固有ベクトルの 2 ノルムは必ずしも 1 である必要はありません。

  B が対称正定値の場合、V の固有ベクトルは、個々の B ノルムが 1 になるように正規化されます。A も対称の場合、固有ベクトルは B と正規直交になります。

マシン、MATLAB^® のリリース、またはパラメーター (開始ベクトル、部分空間の次元など) が異なる場合、異なる固有ベクトルが出力されることがありますが、数値的にはいずれも正確です。

• 実数固有ベクトルでは、固有ベクトルの符号を変更できます。

• 複素数固有ベクトルでは、絶対値が 1 の任意の複素数を固有ベクトルに乗算できます。

• 重複固有値では、その固有ベクトルを線形結合によって再結合できます。たとえば、Ax = λx かつ Ay = λy の場合、A(x+y) = λ(x+y) であるため、x+y も A の固有ベクトルです。

D — 固有値の行列

行列

固有値の行列。主対角に固有値をもつ対角行列として返されます。

flag — 収束フラグ

0 | 1

収束フラグ。0 または 1 として返されます。0 の値はすべての固有値が収束したことを示します。それ以外の場合は、一部の固有値が収束していません。

この収束フラグ出力を使用すると、失敗した収束に関する警告が非表示になります。

ヒント

• eigs は、複数の実行にわたって再現性を確保するために、プライベート乱数ストリームを使用して既定の開始ベクトルを生成します。eigs を呼び出す前に rng を使用して乱数発生器の状態を設定しても、出力に影響しません。

• eigs の使用は、小規模で密な行列でいくつかの固有値を求めるための方法として最も効率的ではありません。このような問題では、eig(full(A)) を使用する方が迅速な場合があります。たとえば、500 行 500 列の行列の固有値を 3 つ求める問題は比較的小規模なので、eig で容易に処理できます。

• 指定した行列について eigs が収束しない場合は、'SubspaceDimension' の値を増やすことによって Lanczos 基底ベクトルの数を増加させます。補助的な選択肢として、反復の最大回数 'MaxIterations' と収束の許容誤差 'Tolerance' を調整することも、収束動作に役立つ場合があります。

参照

[1] Stewart, G.W. "A Krylov-Schur Algorithm for Large Eigenproblems." SIAM Journal of Matrix Analysis and Applications. Vol. 23, Issue 3, 2001, pp. 601–614.

[2] Lehoucq, R.B., D.C. Sorenson, and C. Yang. ARPACK Users' Guide. Philadelphia, PA: SIAM, 1998.

拡張機能

スレッドベースの環境

MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。

この関数はスレッドベースの環境を完全にサポートしています。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。

分散配列

Parallel Computing Toolbox™ を使用して、クラスターの結合メモリ上で大きなアレイを分割します。

使用上の注意および制限:

• 入力行列 A と B の型は double でなければなりません。

詳細については、分散配列を使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2006a より前に導入

R2025a: 単精度の入力引数の指定

以下の引数は単精度として指定できます。

• A、B — 入力行列

• sigma — 固有値のタイプ

• StartVector — 初期開始ベクトル

A、B、または StartVector を単精度として指定すると、関数は単精度で計算を行い、single 型の出力を返します。

行列関数 Afun と行列サイズ n のみを入力として指定すると、eigs の出力の精度は Afun の出力と同じになります。また、B または StartVector のいずれかを single として指定する場合、Afun の出力も single でなければなりません。

R2017b: 動作とアルゴリズムの変更

• 出力の並べ替え順序の変更

  eigs は、sigma の値に従って出力を並べ替えるようになりました。たとえば、eigs(A,k,'largestabs') コマンドは、k 固有値を大きな値から降順に並べて生成します。

  以前は、eigs によって生成される出力の順序は保証されませんでした。

• 再現性

  eigs を複数回続けて呼び出しても、同じ結果が生成されるようになりました。この動作を変更するには、'StartVector' をランダム ベクトルに設定します。

• 表示

  2 の表示値は、タイミング情報を返さなくなりました。代わりに、eigs は 2 の値を 1 の値と同様に扱います。また、'Display' オプションによって表示されるメッセージも変更されました。新しいメッセージには、Ritz 値ではなく、各反復の残差が表示されます。

参考

eig | svds | cdf2rdf