有限差分ラプラシアン
この例では、L 型領域で有限差分ラプラシアンを計算して表示する方法を示します。
領域
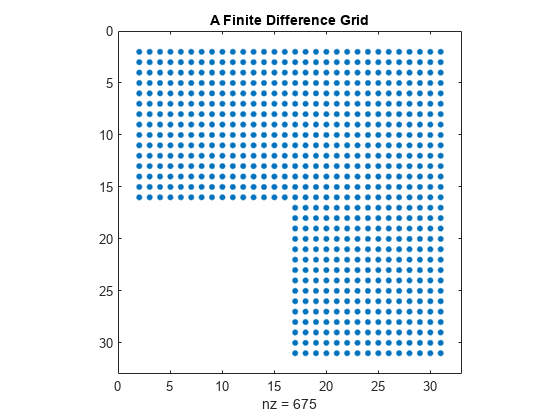
関数 numgrid は、L 型領域内の点に番号を付けます。関数 spy は、行列内の非ゼロの要素のパターンを可視化するためのとても役立つツールです。これら 2 つの関数を使用して、L 型領域を生成して表示します。
n = 32; R = 'L'; G = numgrid(R,n); spy(G) title('A Finite Difference Grid')
サンプルとして、小さい行列のバージョンを示します。
g = numgrid(R,10)
g = 10×10
0 0 0 0 0 0 0 0 0 0
0 1 5 9 13 17 25 33 41 0
0 2 6 10 14 18 26 34 42 0
0 3 7 11 15 19 27 35 43 0
0 4 8 12 16 20 28 36 44 0
0 0 0 0 0 21 29 37 45 0
0 0 0 0 0 22 30 38 46 0
0 0 0 0 0 23 31 39 47 0
0 0 0 0 0 24 32 40 48 0
0 0 0 0 0 0 0 0 0 0
離散ラプラシアン
離散ラプラシアンを生成するために delsq を使用します。関数 spy を再度使用して行列要素のグラフィカルな表現を取得します。
D = delsq(G);
spy(D)
title('The 5-Point Laplacian')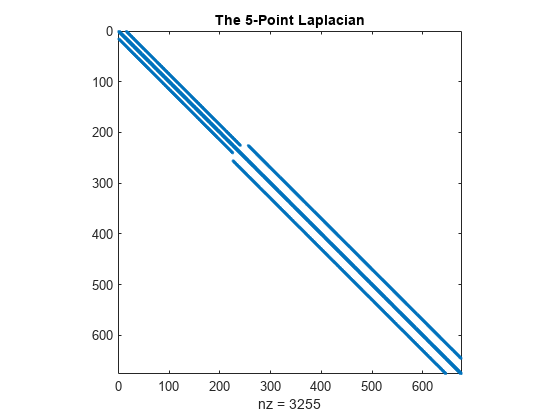
内部点の数を決定します。
N = sum(G(:)>0)
N = 675
ディリクレの境界値問題
スパースの線形システムに対するディリクレの境界値問題を解きます。問題設定は次のとおりです。
内部では delsq(u) = 1、境界では u = 0。
rhs = ones(N,1); if (R == 'N') % For nested dissection, turn off minimum degree ordering. spparms('autommd',0) u = D\rhs; spparms('autommd',1) else u = D\rhs; % This is used for R=='L' as in this example end
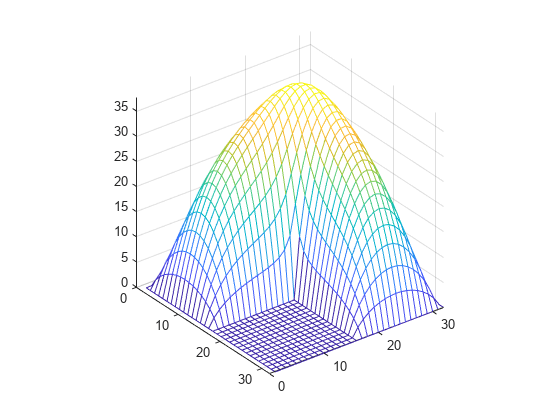
L 型グリッド上に解を写像し、等高線図としてプロットします。
U = G; U(G>0) = full(u(G(G>0))); clabel(contour(U)); prism axis square ij

メッシュ プロットとして解を示します。
mesh(U) axis([0 n 0 n 0 max(max(U))]) axis square ij