グラフと行列

この例では、スパース行列の適用を示してグラフと行列の関係について説明します。

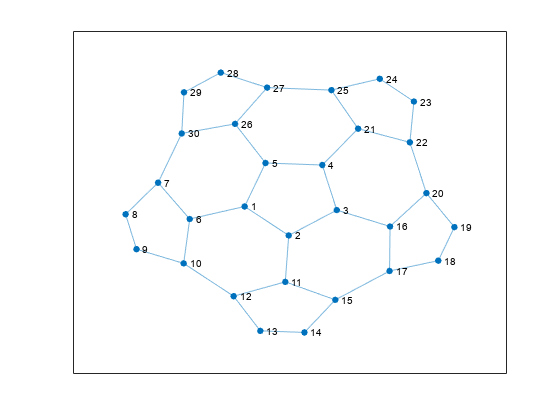
グラフは、ノード間の連結、すなわちエッジが指定されたノードの集合です。グラフには、多くの形状とサイズがあります。1 つの例としては、Buckminster Fuller の測地線ドームの連結グラフがあります。これはサッカー ボールまたは炭素 60 の分子の形状にも見られます。

MATLAB® では、関数 bucky を使用して、測地線ドームのグラフを生成できます。

[B,V] = bucky;
G = graph(B);
p = plot(G);
axis equal

また、ノードの座標を指定することで、このグラフの表示を変更できます。

p.XData = V(:,1);
p.YData = V(:,2);

関数 bucky は隣接行列を返すため、グラフの作成に使用できます。隣接行列は、グラフのノードとエッジを表現する方法の 1 つです。

グラフの隣接行列を作るために、ノードに 1 から N の番号を付けます。そして、ノード i がノード j と連結している場合、N 行 N 列の行列の各要素 (i,j) を 1 に設定し、そうでない場合は 0 にします。したがって、無向グラフの場合は隣接行列が対称になりますが、有向グラフの場合は必ずしもそうはなりません。

たとえば、次に示すのは単純グラフと、関連する隣接行列です。

% Define a matrix A.
A = [0 1 1 0 ; 1 0 0 1 ; 1 0 0 1 ; 0 1 1 0];

% Draw a picture showing the connected nodes.
cla
subplot(1,2,1);
gplot(A,[0 1;1 1;0 0;1 0],'.-');
text([-0.2, 1.2 -0.2, 1.2],[1.2, 1.2, -.2, -.2],('1234')', ...
   'HorizontalAlignment','center')
axis([-1 2 -1 2],'off')

% Draw a picture showing the adjacency matrix.
subplot(1,2,2);
xtemp = repmat(1:4,1,4);
ytemp = reshape(repmat(1:4,4,1),16,1)';
text(xtemp-.5,ytemp-.5,char('0'+A(:)),'HorizontalAlignment','center');
line([.25 0 0 .25 NaN 3.75 4 4 3.75],[0 0 4 4 NaN 0 0 4 4])
axis off tight

スパース行列は、非常に大きなグラフを表現する場合に特に便利です。これは、通常各ノードが他のいくつかのノードとのみ接続されるためです。その結果、多くの場合、隣接行列の非ゼロ要素の密度は大きなグラフに対して比較的小さくなります。バッキー ボール隣接行列は、180 個のみの非ゼロ要素を含む 60 行 60 列の対称スパース行列であるため、良い例です。この行列の密度はわずか 5% です。

隣接行列によってこのグラフを定義しているため、隣接行列の要素のサブセットを使用してバッキー ボールの一部をプロットできます。

関数 adjacency を使用して、グラフに使用する新しい隣接行列を作成します。隣接行列にインデックスを付けることにより、バッキー ボールの片方の半球にあるノードを表示して、新しい小さなグラフを作成します。

figure
A = adjacency(G);
H = graph(A(1:30,1:30));
h = plot(H);

この半球の隣接行列を可視化するために、関数 spy を使用して隣接行列の非ゼロ要素の輪郭をプロットします。

この行列は、ノード i がノード j と接する場合、ノード j はノード i と接するため、対称行列になります。

spy(A(1:30,1:30))
title('Top Left Corner of Bucky Ball Adjacency Matrix')

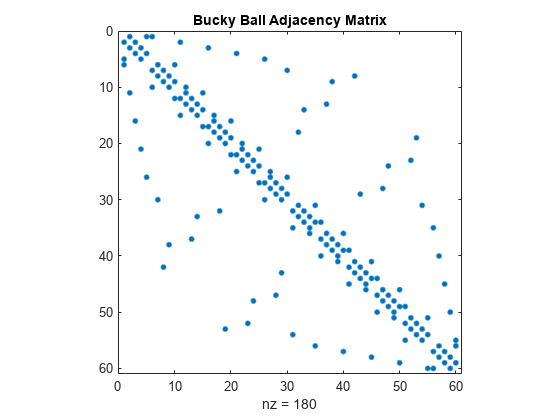
最終的に、バッキー ボール隣接行列全体の spy プロットは次のようになります。

spy(A)
title('Bucky Ball Adjacency Matrix')

参考

spy | graph