symmlq

線形方程式系の求解 — 対称 LQ 法

構文

x = symmlq(A,b)

x = symmlq(A,b,tol)

x = symmlq(A,b,tol,maxit)

x = symmlq(A,b,tol,maxit,M)

x = symmlq(A,b,tol,maxit,M1,M2)

x = symmlq(A,b,tol,maxit,M1,M2,x0)

[x,flag] = symmlq(___)

[x,flag,relres] = symmlq(___)

[x,flag,relres,iter] = symmlq(___)

[x,flag,relres,iter,resvec] = symmlq(___)

[x,flag,relres,iter,resvec,resveccg] = symmlq(___)

説明

x = symmlq(A,b) は、対称 LQ 法を使用して、線形方程式系 A*x = b を x について解きます。試行が正常に完了した場合、symmlq は収束を確認するメッセージを表示します。symmlq が最大反復回数に達しても収束しないか、何らかの理由で実行を停止した場合は、相対残差 norm(b-A*x)/norm(b) と停止時の反復回数を含む診断メッセージが表示されます。

x = symmlq(A,b,tol) は、このメソッドの許容誤差を指定します。既定の許容誤差は 1e-6 です。

x = symmlq(A,b,tol,maxit) は、使用する最大反復回数を指定します。symmlq は、maxit 以内の反復で収束しない場合、診断メッセージを表示します。

x = symmlq(A,b,tol,maxit,M) は前処理行列 M を指定し、y について系 $$H^{-1}A{H}^{-T}y=H^{-1}b$$ を実質的に解くことにより x を計算します。ここで、$$y=H^{T}x$$ および $$H=M^{1/2}={\left(M_1{M}_2\right)}^{1/2}$$ です。アルゴリズムは H を明示的に形成しません。前処理行列を使用すると、問題の数値的なプロパティと計算の効率を向上させることができます。

x = symmlq(A,b,tol,maxit,M1,M2) は M = M1*M2 となるような前処理行列 M の因子を指定します。

x = symmlq(A,b,tol,maxit,M1,M2,x0) は解のベクトル x の初期推定を指定します。既定値はゼロのベクトルです。

[x,flag] = symmlq(___) は、アルゴリズムが正常に収束したかどうかを示すフラグを返します。flag = 0 の場合、収束は正常に実行されています。この出力構文は、前記のすべての入力引数の組み合わせで使用できます。flag 出力を指定する場合、symmlq は診断メッセージを表示しません。

[x,flag,relres] = symmlq(___) は、計算された解の残差誤差も返します。flag が 0 の場合は、relres <= tol になります。

[x,flag,relres,iter] = symmlq(___) は、x が計算されたときの反復回数 iter も返します。

[x,flag,relres,iter,resvec] = symmlq(___) は、各反復で、最初の残差 norm(b-A*x0) を含む残差ノルムのベクトルも返します。

[x,flag,relres,iter,resvec,resveccg] = symmlq(___) は、各反復で共役勾配法の残差ノルムのベクトルも返します。

例

線形システムの反復法

既定の設定で symmlq を使用して正方線形システムを解いてから、解法プロセスで使用される許容誤差と反復回数を調整します。

スパース三重対角行列 A を、係数行列として作成します。$\mathrm{Ax}=\mathit{b}$ の右辺に $\mathit{A}$ の密な行の合計をベクトルとして使用し、解 $\mathit{x}$ が 1 のベクトルとなると想定されるようにします。

n = 400; 
on = ones(n,1); 
A = spdiags([-2*on 4*on -2*on],-1:1,n,n);
b = full(sum(A,2));

symmlq を使用して $\mathrm{Ax}=\mathit{b}$ を解きます。出力の表示には相対残差誤差 $\frac{\Vert \mathit{b}-\mathrm{Ax}\Vert }{\Vert \mathit{b}\Vert }$ の値が含まれます。

x = symmlq(A,b);

symmlq stopped at iteration 20 without converging to the desired tolerance 1e-06
because the maximum number of iterations was reached.
The iterate returned (number 20) has relative residual 0.045.

既定では symmlq は 20 回の反復と 1e-6 の許容誤差を使用し、アルゴリズムはこの行列について、その 20 回の反復内で収束できません。残差が 1e-2 程度であり、これはより多くの反復が必要であることをよく示しています。より大きな許容誤差を使用して、アルゴリズムの収束をより簡単にすることもできます。

1e-4 の許容誤差と 250 回の反復を使用して、再度方程式系を解きます。

x = symmlq(A,b,1e-4,250);

symmlq converged at iteration 199 to a solution with relative residual 1.5e-14.

前処理行列を使用した symmlq の使用

線形システムを解くために前処理行列を symmlq と使用する効果を調べます。

対称正定値の、バンド係数行列を作成します。

A = delsq(numgrid('S',102));

$\mathrm{Ax}=\mathit{b}$ に対する真の解がすべて 1 のベクトルになるように、b を定義します。

b = sum(A,2);

許容誤差と最大反復回数を設定します。

tol = 1e-12;
maxit = 100;

symmlq を使用して、要求された許容誤差と反復回数で解を求めます。この求解プロセスについての情報を返す 6 つの出力を指定します。

• x は A*x = b の計算された解です。

• fl0 はアルゴリズムが収束したかどうかを示すフラグです。

• rr0 は計算解 x の相対残差です。

• it0 は x が計算されたときの反復回数です。

• rv0 は $\Vert \mathit{b}-\mathrm{Ax}\Vert$ の残差履歴のベクトルです。

• rvcg0 は $\Vert {\mathit{A}}^{\mathit{T}}\mathit{A}\mathit{x}-{\mathit{A}}^{\mathit{T}}\mathit{b}\Vert$ の共役勾配残差履歴のベクトルです。

[x,fl0,rr0,it0,rv0,rvcg0] = symmlq(A,b,tol,maxit);
fl0

fl0 = 1

rr0

rr0 = 0.0031

it0

it0 = 100

fl0 は、symmlq が要求した反復回数 100 回以内に要求した許容誤差 1e-12 に収束しなかったため、1 となります。

収束を助けるため、前処理行列を指定できます。A は対称であるため、ichol を使用して前処理行列 $\mathit{M}=\mathit{L}{\mathit{L}}^{\mathit{T}}$ を生成します。'ict' オプションを指定してしきい値棄却による不完全コレスキー分解を使用し、1e-6 の対角シフト値を指定して非正のピボットを回避します。symmlq への入力として L および L' を指定して、前処理された方程式系を解きます。

setup = struct('type','ict','diagcomp',1e-6,'droptol',1e-14);
L = ichol(A,setup);
[x1,fl1,rr1,it1,rv1,rvcg1] = symmlq(A,b,tol,maxit,L,L');
fl1

fl1 = 0

rr1

rr1 = 2.5625e-15

it1

it1 = 3

ichol 前処理行列を使用すると、問題の数値特性が大きく改善され、symmlq はより迅速に収束することができます。出力 rv1(1) は norm(b)、出力 rv1(end) は norm(b-A*x1) になります。

各反復での相対残差をプロットして、symmlq の進行状況を確認できます。各解の共役勾配の残差履歴を、指定された許容誤差の線とともにプロットします。

semilogy(0:length(rvcg0)-1,rvcg0/norm(b),'-o')
hold on
semilogy(0:length(rvcg1)-1,rvcg1/norm(b),'-o')
yline(tol,'r--');
legend('No preconditioner','ICHOL preconditioner','Tolerance','Location','SouthEast')
xlabel('Iteration number')
ylabel('Relative residual')

初期推定の指定

symmlq に解の初期推定を指定する効果を調べます。

三重対角スパース行列を作成します。$\mathit{x}$ の想定される解が 1 のベクトルとなるよう、$\mathrm{Ax}=\mathit{b}$ の右辺のベクトルとして各行の合計を使用します。

n = 900;
e = ones(n,1);
A = spdiags([e 2*e e],-1:1,n,n);
b = sum(A,2);

symmlq を使用して $\mathrm{Ax}=\mathit{b}$ を 2 回解きます。1 回は既定の初期推定、もう 1 回は解の適切な初期推定を使用します。両方の解に対して 200 回の反復と既定の許容誤差を使用します。すべての要素が 0.99 と等価のベクトルとして初期推定を 2 番目の解に指定します。

maxit = 200;
x1 = symmlq(A,b,[],maxit);

symmlq converged at iteration 34 to a solution with relative residual 9.5e-07.

x0 = 0.99*e;
x2 = symmlq(A,b,[],maxit,[],[],x0);

symmlq converged at iteration 6 to a solution with relative residual 8.7e-07.

この場合、初期推定を指定すると symmlq をより迅速に収束させることができます。

中間結果を返す

for ループで symmlq を呼び出して、初期推定を使用して中間結果を取得することもできます。ソルバーを呼び出すたびに、数回の反復が行われ、計算された解が格納されます。その後、その解を次の反復のバッチに対する初期ベクトルとして使用します。

たとえば、次のコードは 100 回の反復を 4 回実行し、for ループを通過するたびに、解のベクトルを格納します。

x0 = zeros(size(A,2),1);
tol = 1e-8;
maxit = 100;
for k = 1:4
    [x,flag,relres] = symmlq(A,b,tol,maxit,[],[],x0);
    X(:,k) = x;
    R(k) = relres;
    x0 = x;
end

X(:,k) は、for ループの反復 k で計算された解のベクトルであり、R(k) はその解の相対残差です。

数値行列に代わる関数ハンドルの使用

symmlq に、係数行列 A の代わりに A*x を計算する関数ハンドルを与えて線形システムを解きます。

gallery で生成されたウィルキンソンのテスト行列の 1 つは 21 行 21 列の三重対角行列です。行列をプレビューします。

A = gallery('wilk',21)

A = 21×21

    10     1     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0
     1     9     1     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0
     0     1     8     1     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0
     0     0     1     7     1     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0
     0     0     0     1     6     1     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0
     0     0     0     0     1     5     1     0     0     0     0     0     0     0     0     0     0     0     0     0     0
     0     0     0     0     0     1     4     1     0     0     0     0     0     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     1     3     1     0     0     0     0     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     1     2     1     0     0     0     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0     1     1     1     0     0     0     0     0     0     0     0     0     0
      ⋮

ウィルキンソン行列の構造は特殊なため、演算 A*x を関数ハンドルで表すことができます。A がベクトルを乗算する場合、結果のベクトルのほとんどの要素はゼロとなります。結果の非ゼロ要素は、A の非ゼロの三重対角要素に対応します。さらに、主対角のみに 1 と等しくない非ゼロ要素があります。

式 $\mathrm{Ax}$ は次のようになります。

$\mathrm{Ax}=\left[\begin{array}{cccccccccc}10& 1& 0& \cdots & & \cdots & & \cdots & 0& 0\\ 1& 9& 1& 0& & & & & & 0\\ 0& 1& 8& 1& 0& & & & & ⋮\\ ⋮& 0& 1& 7& 1& 0& & & & \\ & & 0& 1& 6& 1& 0& & & ⋮\\ ⋮& & & 0& 1& 5& 1& 0& & \\ & & & & 0& 1& 4& 1& 0& ⋮\\ ⋮& & & & & 0& 1& 3& \ddots & 0\\ 0& & & & & & 0& \ddots & \ddots & 1\\ 0& 0& \cdots & & \cdots & & \cdots & 0& 1& 10\end{array}\right]\left[\begin{array}{c}{\mathit{x}}_1\\ {\mathit{x}}_2\\ {\mathit{x}}_3\\ {\mathit{x}}_4\\ {\mathit{x}}_5\\ ⋮\\ \\ ⋮\\ \\ {\mathit{x}}_{21}\end{array}\right]=\left[\begin{array}{c}10{\mathit{x}}_1+{\mathit{x}}_2\\ {\mathit{x}}_1+9{\mathit{x}}_2+{\mathit{x}}_3\\ {\mathit{x}}_2+8{\mathit{x}}_3+{\mathit{x}}_4\\ ⋮\\ {\mathit{x}}_{19}+9{\mathit{x}}_{20}+{\mathit{x}}_{21}\\ {\mathit{x}}_{20}+10{\mathit{x}}_{21}\end{array}\right]$.

結果のベクトルは、3 つのベクトルの合計として記述できます。

$\mathrm{Ax}=\left[\begin{array}{c}0+10{\mathit{x}}_1+{\mathit{x}}_2\\ {\mathit{x}}_1+9{\mathit{x}}_2+{\mathit{x}}_3\\ {\mathit{x}}_2+8{\mathit{x}}_3+{\mathit{x}}_4\\ ⋮\\ {\mathit{x}}_{19}+9{\mathit{x}}_{20}+{\mathit{x}}_{21}\\ {\mathit{x}}_{20}+10{\mathit{x}}_{21}+0\end{array}\right]$=$\left[\begin{array}{c}0\\ {\mathit{x}}_1\\ ⋮\\ {\mathit{x}}_{20}\end{array}\right]+\left[\begin{array}{c}10{\mathit{x}}_1\\ 9{\mathit{x}}_2\\ ⋮\\ 10{\mathit{x}}_{21}\end{array}\right]+\left[\begin{array}{c}{\mathit{x}}_2\\ ⋮\\ {\mathit{x}}_{21}\\ 0\end{array}\right]$

MATLAB® で、これらのベクトルを作成および合算することにより A*x の値を与える関数を記述します。

function y = afun(x)
y = [0; x(1:20)] + ...
    [(10:-1:0)'; (1:10)'].*x + ...
    [x(2:21); 0];
end

(この関数は、ローカル関数として例の最後に保存されています)

ここで、symmlq に A*x を計算する関数ハンドルを与えて、線形システム $\mathrm{Ax}=\mathit{b}$ を解きます。1e-12 の許容誤差と 50 回の反復を使用します。

b = ones(21,1);
tol = 1e-12;  
maxit = 50;
x1 = symmlq(@afun,b,tol,maxit)

symmlq converged at iteration 10 to a solution with relative residual 4.5e-16.

x1 = 21×1

    0.0910
    0.0899
    0.0999
    0.1109
    0.1241
    0.1443
    0.1544
    0.2383
    0.1309
    0.5000
      ⋮

afun(x1) が 1 のベクトルを生成していることを確認します。

afun(x1)

ans = 21×1

    1.0000
    1.0000
    1.0000
    1.0000
    1.0000
    1.0000
    1.0000
    1.0000
    1.0000
    1.0000
      ⋮

ローカル関数

function y = afun(x)
y = [0; x(1:20)] + ...
    [(10:-1:0)'; (1:10)'].*x + ...
    [x(2:21); 0];
end

入力引数

A — 係数行列

行列 | 関数ハンドル

係数行列。対称行列または関数ハンドルとして指定します。この行列は線形システム A*x = b の係数行列です。一般に、A は大規模なスパース行列、または大規模なスパース行列と列ベクトルの積を返す関数ハンドルです。issymmetric を使用して A が対称であることを確認できます。

関数ハンドルとしての A の指定

オプションで、係数行列を、行列ではなく関数ハンドルとして指定できます。この関数ハンドルは、係数行列全体を作成するのではなく、行列とベクトルの積を返し、計算をより効率的にします。

関数ハンドルを使用するには、関数シグネチャ function y = afun(x) を使用します。関数のパラメーター化では、必要な場合に関数 afun に追加のパラメーターを指定する方法を説明しています。関数呼び出し afun(x) は A*x の値を返さなければなりません。

データ型: double | function_handle
複素数のサポート: あり

b — 線形方程式の右辺

列ベクトル

線形方程式の右辺。列ベクトルとして指定します。b の長さは size(A,1) と等しくなければなりません。

データ型: double
複素数のサポート: あり

tol — メソッドの許容誤差

[] または 1e-6 (既定値) | 正のスカラー

メソッドの許容誤差。正のスカラーとして指定します。この入力を使用して計算の精度と実行時間とをトレードオフします。成功するには、symmlq は、許容される反復回数内に許容誤差を満たさなければなりません。tol を小さい値にすると、解がより正確でなければ計算が成功しないことを意味します。

データ型: double

maxit — 最大反復回数

[] または min(size(A,1),20) (既定値) | 正のスカラー整数

最大反復回数。正のスカラー整数として指定します。maxit の値を増やして、symmlq が許容誤差 tol を満たすためにより多くの反復を行えるようにします。一般に、tol の値が小さいほど、計算を正常に完了するための反復がより多く必要であるということを意味します。

M, M1, M2 — 前処理行列 (個別の引数として)

eye(size(A)) (既定値) | 行列 | 関数ハンドル

前処理行列。行列または関数ハンドルの個別の引数として指定します。前処理行列 M またはその行列の因子 M = M1*M2 を指定して線形システムの数値的側面を改善し、symmlq での迅速な収束を容易にします。不完全行列因数分解関数 ilu および ichol を使用して前処理行列を生成できます。また、因数分解の前に equilibrate を使用して、係数行列の条件数を改善できます。前処理行列の詳細については、線形方程式の反復法を参照してください。

symmlq は指定なし前処理行列を単位行列として扱います。

関数ハンドルとしての M の指定

オプションで、M、M1 または M2 のいずれかを、行列ではなく関数ハンドルとして指定できます。関数ハンドルは、前処理行列全体を作成するのではなく行列ベクトル演算を行い、計算をより効率化します。

関数ハンドルを使用するには、関数シグネチャ function y = mfun(x) を使用します。関数のパラメーター化では、必要な場合に関数 mfun に追加のパラメーターを指定する方法を説明しています。関数呼び出し mfun(x) は M\x または M2\(M1\x) の値を返さなければなりません。

データ型: double | function_handle
複素数のサポート: あり

x0 — 初期推定

[] またはゼロの列ベクトル (既定値) | 列ベクトル

初期推定。size(A,2) に等しい長さの列ベクトルとして指定します。symmlq に、既定値のゼロのベクトルではなく、より妥当な初期推定 x0 を与えることができれば、計算時間が節約でき、アルゴリズムがより速く収束するようにできます。

データ型: double
複素数のサポート: あり

出力引数

x — 線形システムの解

列ベクトル

線形システムの解。列ベクトルとして返されます。この出力は線形システム A*x = b の近似解を与えます。計算が正常に完了した場合 (flag = 0)、relres は tol 以下になります。

計算が正常に完了しない場合 (flag ~= 0) は常に、symmlq によって返される解 x は、すべての反復にわたり計算された最小残差ノルムをもちます。

flag — 収束フラグ

スカラー

収束フラグ。次の表のいずれかのスカラー値として返されます。収束フラグは、計算が正常に実行されたかどうかを示し、さまざまな失敗の形式を区別します。

フラグの値	収束
0	成功 — symmlq は希望する許容誤差 tol に反復回数 maxit 以内で収束しました。
1	失敗 — symmlq は maxit 回の反復を行いましたが収束しませんでした。
2	失敗 — 前処理行列 M または M = M1*M2 が悪条件になっています。
3	失敗 — 連続する 2 回の反復が同じであり、symmlq は計算を進めていません。
4	失敗 — symmlq アルゴリズムで計算されたスカラー量の 1 つが、計算を続けるには大きすぎるかまたは小さすぎます。
5	失敗 — 前処理行列 M は対称正定値ではありません。

relres — 相対残差誤差

スカラー

相対残差誤差。スカラーとして返されます。相対残差誤差は、返された答え x がどれだけ正確かを示すものです。symmlq は、求解のプロセスの各反復で相対残差および共役勾配残差を追跡し、"いずれかの" 残差が指定された許容誤差 tol を満たしたときにアルゴリズムは収束します。relres の出力には、相対残差または共役勾配残差のいずれかの、収束した残差の値が含まれます。

• 相対残差誤差は norm(b-A*x)/norm(b) に等しく、一般には、symmlq が収束するときの許容誤差 tol を満たす残差です。resvec の出力は、すべての反復にわたってこの残差の履歴を追跡します。

• 共役勾配残差誤差は norm(A'*A*x - A'*b) に等しくなります。この残差は symmlq が収束する回数が相対残差よりも少なくなる原因となります。resveccg の出力は、すべての反復にわたってこの残差の履歴を追跡します。

データ型: double

iter — 反復回数

スカラー

反復回数。スカラーとして返されます。この出力は、x に対する計算解が計算された時点での反復回数を示します。

データ型: double

resvec — 残差誤差

ベクトル

残差誤差。ベクトルとして返されます。残差誤差 norm(b-A*x) によって、アルゴリズムが x の特定の値に対する収束にどの程度近いかがわかります。resvec の要素数は反復の回数と同じです。resvec の内容を調べて、tol または maxit の値を変更するかどうかを決定することができます。

データ型: double

resveccg — 共役勾配残差ノルム

ベクトル

共役勾配残差ノルム。ベクトルとして返されます。resveccg の要素数は反復の回数と同じです。

データ型: double

詳細

対称 LQ 法

MINRES 法と SYMMLQ 法は、共役勾配法 PCG の基盤となっている Lanczos 法の変形です。PCG と同様に、係数行列は対称である必要はありますが、MINRES と SYMMLQ は不定でも構いません (すべての固有値が正でなくてもよい)。これは、Lanczos 法で通常みられる暗黙的な LU 分解を回避することで実現されます。これはゼロのピボットが起きたときに、ブレークダウンが発生しやすくなります。

MINRES は 2 ノルムの残差を最小化しますが、SYMMLQ は LQ 分解を使用して射影システムを解き、残差を以前のすべての残差と直交したままにします[1]。

ヒント

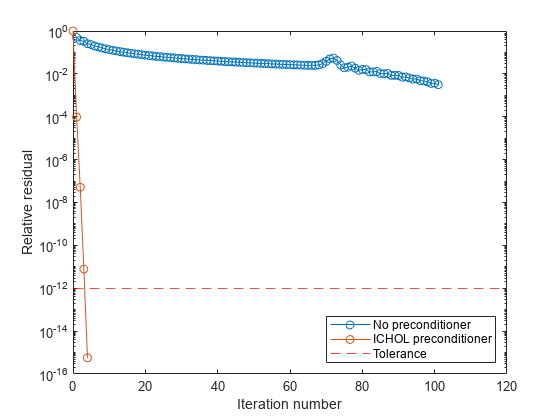
• ほとんどの反復メソッドにおける収束は、係数行列の条件数 cond(A) に依存します。A が正方行列の場合、equilibrate を使用して条件数を改善することができ、それ自体でほとんどの反復ソルバーが収束しやすくなります。ただし、equilibrate を使用することでも、平衡化した行列 B = R*P*A*C を次に因子分解する際に前処理行列の品質が向上します。

• dissect や symrcm などの行列の並べ替え関数を使用して係数行列の行と列を並べ替え、係数行列が因子分解されて前処理行列が生成される際に非ゼロの数を最小化できます。これによって、後で前処理を使用した線形システムを解くのに必要なメモリと時間を削減できます。

参照

[1] Barrett, R., M. Berry, T. F. Chan, et al., Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, SIAM, Philadelphia, 1994.

[2] Paige, C. C. and M. A. Saunders, "Solution of Sparse Indefinite Systems of Linear Equations." SIAM J. Numer. Anal., Vol.12, 1975, pp. 617-629.

拡張機能

スレッドベースの環境

MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。

この関数はスレッドベースの環境を完全にサポートしています。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。

分散配列

Parallel Computing Toolbox™ を使用して、クラスターの結合メモリ上で大きなアレイを分割します。

使用上の注意事項および制限事項:

• M1 が関数である場合は、各行に個別に適用されます。

詳細については、分散配列を使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2006a より前に導入

参考

bicg | bicgstab | cgs | gmres | lsqr | minres | pcg | qmr | mldivide

トピック

• 線形方程式の反復法