lsqr

線形方程式系の求解 — 最小二乗法

構文

x = lsqr(A,b)

x = lsqr(A,b,tol)

x = lsqr(A,b,tol,maxit)

x = lsqr(A,b,tol,maxit,M)

x = lsqr(A,b,tol,maxit,M1,M2)

x = lsqr(A,b,tol,maxit,M1,M2,x0)

[x,flag] = lsqr(___)

[x,flag,relres] = lsqr(___)

[x,flag,relres,iter] = lsqr(___)

[x,flag,relres,iter,resvec] = lsqr(___)

[x,flag,relres,iter,resvec,lsvec] = lsqr(___)

説明

x = lsqr(A,b) は最小二乗法を使用して x について線形方程式系 A*x = b を解きます。lsqr は、norm(b-A*x) を最小化する x についての最小二乗解を求めます。A が定数である場合、最小二乗解は線形システムの解でもあります。試行が正常に完了した場合、lsqr は収束を確認するメッセージを表示します。lsqr が最大反復回数に達しても収束しないか、何らかの理由で実行を停止した場合は、相対残差 norm(b-A*x)/norm(b) と停止時の反復回数を含む診断メッセージが表示されます。

x = lsqr(A,b,tol) は、このメソッドの許容誤差を指定します。既定の許容誤差は 1e-6 です。

x = lsqr(A,b,tol,maxit) は、使用する最大反復回数を指定します。lsqr は、maxit 以内の反復で収束しない場合、診断メッセージを表示します。

x = lsqr(A,b,tol,maxit,M) は前処理行列 M を指定し、y について系 $$A{M}^{-1}y=b$$ を実質的に解くことにより x を計算します。ここで、$$y=Mx$$ です。前処理行列を使用すると、問題の数値的なプロパティと計算の効率を向上させることができます。

x = lsqr(A,b,tol,maxit,M1,M2) は M = M1*M2 となるような前処理行列 M の因子を指定します。

x = lsqr(A,b,tol,maxit,M1,M2,x0) は解のベクトル x の初期推定を指定します。既定値はゼロのベクトルです。

[x,flag] = lsqr(___) は、アルゴリズムが正常に収束したかどうかを示すフラグを返します。flag = 0 の場合、収束は正常に実行されています。この出力構文は、前記のすべての入力引数の組み合わせで使用できます。flag 出力を指定する場合、lsqr は診断メッセージを表示しません。

また、[x,flag,relres] = lsqr(___) は、計算された解 x の残差誤差を返します。flag が 0 の場合、x は norm(b-A*x) を最小化する最小二乗解です。relres が小さい場合、x も定数の解です。これは、relres が norm(b-A*x)/norm(b) を表すためです。

[x,flag,relres,iter] = lsqr(___) は、x が計算されたときの反復回数 iter も返します。

[x,flag,relres,iter,resvec] = lsqr(___) は、各反復で、最初の残差 norm(b-A*x0) を含む残差ノルムのベクトルも返します。

[x,flag,relres,iter,resvec,lsvec] = lsqr(___) はまた lsvec を返します。これは、各反復でのスケーリングされた正規方程式の誤差の推定です。

例

線形システムの反復法

lsqr を既定の設定で使用して方形線形システムを解き、次にその求解のプロセスで使用される許容誤差と反復の回数を調整します。

密度が 50% の乱数スパース行列 A を作成します。また、$\mathrm{Ax}=\mathit{b}$ の右辺に乱数のベクトル b を作成します。

rng default
A = sprand(400,300,.5);
b = rand(400,1);

lsqr を使用して $\mathrm{Ax}=\mathit{b}$ を解きます。出力の表示には相対残差誤差 $\frac{\Vert \mathit{b}-\mathrm{Ax}\Vert }{\Vert \mathit{b}\Vert }$ の値が含まれます。

x = lsqr(A,b);

lsqr stopped at iteration 20 without converging to the desired tolerance 1e-06
because the maximum number of iterations was reached.
The iterate returned (number 20) has relative residual 0.26.

既定では lsqr は 20 回の反復と 1e-6 の許容誤差を使用しますが、アルゴリズムではこの行列についてはその 20 回の反復で収束できません。残差がまだ大きいため、より多くの反復 (または前処理行列) が必要であることを示しています。より大きな許容誤差を使用して、アルゴリズムの収束をより簡単にすることもできます。

1e-4 の許容誤差と 70 回の反復を使用して、再度方程式系を解きます。計算された解の相対残差 relres を返す 6 つの出力を、残差履歴 resvec および最小二乗残差履歴 lsvec とともに指定します。

[x,flag,relres,iter,resvec,lsvec] = lsqr(A,b,1e-4,70);
flag

flag = 0

flag が 0 であるため、アルゴリズムは指定された反復回数内に、想定される許容誤差を満たすことができました。一般的に、このようにして、許容誤差と反復回数を共に調整して、速度と精度の間のトレードオフを図ることができます。

計算された解の相対残差と最小二乗残差を調べます。

relres

relres = 0.2625

lsres = lsvec(end)

lsres = 2.7640e-04

これらの残差ノルムは、x が最小二乗解であることを示しています。relres が指定された 1e-4 の許容誤差よりも小さいためです。線形システムに定数解が存在しないため、ソルバーとしての最善は、最小二乗残差が許容誤差を満足するようにすることです。

残差履歴をプロットします。相対残差 resvec は最小値にすばやく到達し、それ以上進むことはできません。一方、最小二乗残差 lsvec は後続の反復で継続して最小化し続けます。

N = length(resvec);
semilogy(0:N-1,lsvec,'--o',0:N-1,resvec,'-o')
legend("Least-squares residual","Relative residual")

前処理行列を使用した lsqr の使用

線形システムを解くために前処理行列を lsqr と使用する効果を調べます。

479 行 479 列の非対称実スパース行列 west0479 を読み込みます。

load west0479
A = west0479;

$\mathrm{Ax}=\mathit{b}$ に対する真の解がすべて 1 のベクトルになるように、b を定義します。

b = sum(A,2);

許容誤差と最大反復回数を設定します。

tol = 1e-12;
maxit = 20;

lsqr を使用して、要求された許容誤差と反復回数で解を求めます。この求解プロセスについての情報を返す 6 つの出力を指定します。

• x は A*x = b の計算された解です。

• fl はアルゴリズムが収束したかどうかを示すフラグです。

• rr は計算解 x の相対残差です。

• it は x が計算されたときの反復回数です。

• rv は $\Vert \mathit{b}-\mathrm{Ax}\Vert$ の残差履歴のベクトルです。

• lsrv は最小二乗残差履歴のベクトルです。

[x,fl,rr,it,rv,lsrv] = lsqr(A,b,tol,maxit);
fl

fl = 1

rr

rr = 0.0017

it

it = 20

fl = 1 であるため、アルゴリズムは最大反復回数内に指定された許容誤差に収束しませんでした。

遅い収束への対応として、前処理行列を指定できます。A は非対称であるため、ilu を使用して前処理行列 $\mathit{M}=\mathit{L}\mathit{U}$ を因数分解形式で生成します。棄却許容誤差を指定して、1e-6 よりも小さい値をもつ非対角エントリを無視します。lsqr への入力として M1 および M2 を L と U に指定することで、$\mathit{y}=\mathrm{Mx}$ の前処理された方程式系 ${\mathrm{AM}}^{-1}\left(\mathit{M}\mathit{x}\right)=\mathit{b}$ を求解します。

setup = struct('type','ilutp','droptol',1e-6);
[L,U] = ilu(A,setup);
[x1,fl1,rr1,it1,rv1,lsrv1] = lsqr(A,b,tol,maxit,L,U);
fl1

fl1 = 0

rr1

rr1 = 7.0954e-14

it1

it1 = 13

ilu 前処理行列を使用すると、13 回目の反復で 1e-12 の所定の許容誤差よりも小さい相対残差が得られます。出力 rv1(1) は norm(b)、出力 rv1(end) は norm(b-A*x1) になります。

各反復での相対残差をプロットして、lsqr の進行状況を確認できます。指定された許容誤差のラインと共に、それぞれの解の残差履歴をプロットします。

semilogy(0:length(rv)-1,rv/norm(b),'-o')
hold on
semilogy(0:length(rv1)-1,rv1/norm(b),'-o')
yline(tol,'r--');
legend('No preconditioner','ILU preconditioner','Tolerance','Location','East')
xlabel('Iteration number')
ylabel('Relative residual')

初期推定の指定

lsqr に解の初期推定を指定する効果を調べます。

乱数の方形スパース行列を作成します。$\mathit{x}$ の想定される解が 1 のベクトルとなるよう、$\mathrm{Ax}=\mathit{b}$ の右辺のベクトルとして各行の合計を使用します。

A = sprand(700,900,0.1);
b = sum(A,2);

lsqr を使用して $\mathrm{Ax}=\mathit{b}$ を 2 回解きます。1 回は既定の初期推定、もう 1 回は解の適切な初期推定を使用します。両方の解に対して 75 回の反復と既定の許容誤差を使用します。すべての要素が 0.99 と等価のベクトルとして初期推定を 2 番目の解に指定します。

maxit = 75;
x1 = lsqr(A,b,[],maxit);

lsqr converged at iteration 64 to a solution with relative residual 8.7e-07.

x0 = 0.99*ones(size(A,2),1);
x2 = lsqr(A,b,[],maxit,[],[],x0);

lsqr converged at iteration 26 to a solution with relative residual 9.6e-07.

初期推定が想定される解に近いため、lsqr はより少ない反復で収束できます。

中間結果を返す

for ループで lsqr を呼び出して、初期推定を使用して中間結果を取得することもできます。ソルバーを呼び出すたびに、数回の反復が行われ、計算された解が格納されます。その後、その解を次の反復のバッチに対する初期ベクトルとして使用します。

たとえば、次のコードは 100 回の反復を 4 回実行し、for ループを通過するたびに、解のベクトルを格納します。

x0 = zeros(size(A,2),1);
tol = 1e-8;
maxit = 100;
for k = 1:4
    [x,flag,relres] = lsqr(A,b,tol,maxit,[],[],x0);
    X(:,k) = x;
    R(k) = relres;
    x0 = x;
end

X(:,k) は、for ループの反復 k で計算された解のベクトルであり、R(k) はその解の相対残差です。

数値行列に代わる関数ハンドルの使用

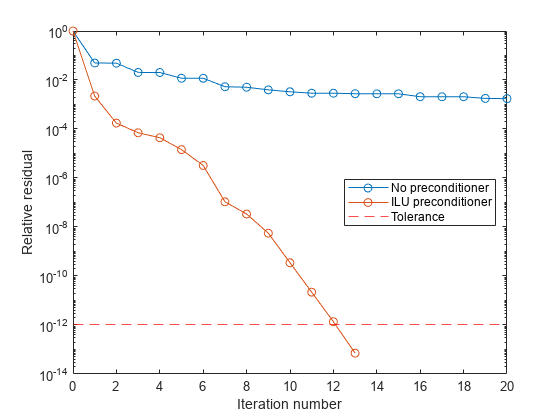
lsqr に、係数行列 A の代わりに A*x および A'*x を計算する関数ハンドルを与えて線形システムを解きます。

非対称の三重対角行列を作成します。行列をプレビューします。

A = gallery('wilk',21) + diag(ones(20,1),1)

A = 21×21

    10     2     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0
     1     9     2     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0
     0     1     8     2     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0
     0     0     1     7     2     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0
     0     0     0     1     6     2     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0
     0     0     0     0     1     5     2     0     0     0     0     0     0     0     0     0     0     0     0     0     0
     0     0     0     0     0     1     4     2     0     0     0     0     0     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     1     3     2     0     0     0     0     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     1     2     2     0     0     0     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0     1     1     2     0     0     0     0     0     0     0     0     0     0
      ⋮

この三重対角行列は特殊な構造であるため、演算 A*x を関数ハンドルで表すことができます。A がベクトルを乗算する場合、結果のベクトルのほとんどの要素はゼロとなります。結果の非ゼロ要素は、A の非ゼロの三重対角要素に対応します。

式 $\mathit{A}\mathit{x}$ は次のようになります。

$\mathit{A}\mathit{x}=\left[\begin{array}{ccccccc}10& 2& 0& \cdots & & \cdots & 0\\ 1& 9& 2& 0& & & ⋮\\ 0& 1& \ddots & 2& 0& & \\ ⋮& 0& 1& 0& \ddots & \ddots & ⋮\\ & & 0& \ddots & 1& \ddots & 0\\ ⋮& & & \ddots & \ddots & \ddots & 2\\ 0& \cdots & & \cdots & 0& 1& 10\end{array}\right]\left[\begin{array}{c}{\mathit{x}}_1\\ {\mathit{x}}_2\\ {\mathit{x}}_3\\ ⋮\\ ⋮\\ {\mathit{x}}_{21}\end{array}\right]=\left[\begin{array}{c}{10\mathit{x}}_1+2{\mathit{x}}_2\\ {\mathit{x}}_1+9{\mathit{x}}_2+2{\mathit{x}}_3\\ ⋮\\ ⋮\\ {\mathit{x}}_{19}+9{\mathit{x}}_{20}+2{\mathit{x}}_{21}\\ {\mathit{x}}_{20}+10{\mathit{x}}_{21}\end{array}\right]$.

結果のベクトルは、3 つのベクトルの合計として記述できます。

$\mathit{A}\mathit{x}=\left[\begin{array}{c}{10\mathit{x}}_1+2{\mathit{x}}_2\\ {\mathit{x}}_1+9{\mathit{x}}_2+2{\mathit{x}}_3\\ ⋮\\ ⋮\\ {\mathit{x}}_{19}+9{\mathit{x}}_{20}+2{\mathit{x}}_{21}\\ {\mathit{x}}_{20}+10{\mathit{x}}_{21}\end{array}\right]$=$\left[\begin{array}{c}0\\ {\mathit{x}}_1\\ {\mathit{x}}_2\\ ⋮\\ {\mathit{x}}_{20}\end{array}\right]+\left[\begin{array}{c}{10\mathit{x}}_1\\ {9\mathit{x}}_2\\ ⋮\\ 9{\mathit{x}}_{20}\\ 10{\mathit{x}}_{21}\end{array}\right]+2\cdot \left[\begin{array}{c}{\mathit{x}}_2\\ {\mathit{x}}_3\\ ⋮\\ {\mathit{x}}_{21}\\ 0\end{array}\right]$

同様に、${\mathit{A}}^{\mathit{T}}\mathit{x}$ の式は次のようになります。

${\mathit{A}}^{\mathit{T}}\mathit{x}=\left[\begin{array}{ccccccc}10& 1& 0& \cdots & & \cdots & 0\\ 2& 9& 1& 0& & & ⋮\\ 0& 2& \ddots & 1& 0& & \\ ⋮& 0& 2& 0& \ddots & \ddots & ⋮\\ & & 0& \ddots & 1& \ddots & 0\\ ⋮& & & \ddots & \ddots & \ddots & 1\\ 0& \cdots & & \cdots & 0& 2& 10\end{array}\right]\left[\begin{array}{c}{\mathit{x}}_1\\ {\mathit{x}}_2\\ {\mathit{x}}_3\\ ⋮\\ ⋮\\ {\mathit{x}}_{21}\end{array}\right]=\left[\begin{array}{c}{10\mathit{x}}_1+{\mathit{x}}_2\\ {2\mathit{x}}_1+9{\mathit{x}}_2+{\mathit{x}}_3\\ ⋮\\ ⋮\\ {2\mathit{x}}_{19}+9{\mathit{x}}_{20}+{\mathit{x}}_{21}\\ {2\mathit{x}}_{20}+10{\mathit{x}}_{21}\end{array}\right]$.

${\mathit{A}}^{\mathit{T}}\mathit{x}=\left[\begin{array}{c}{10\mathit{x}}_1+{\mathit{x}}_2\\ {2\mathit{x}}_1+9{\mathit{x}}_2+{\mathit{x}}_3\\ ⋮\\ ⋮\\ {2\mathit{x}}_{19}+9{\mathit{x}}_{20}+{\mathit{x}}_{21}\\ {2\mathit{x}}_{20}+10{\mathit{x}}_{21}\end{array}\right]=2\cdot \left[\begin{array}{c}0\\ {\mathit{x}}_1\\ {\mathit{x}}_2\\ ⋮\\ {\mathit{x}}_{20}\end{array}\right]+\left[\begin{array}{c}{10\mathit{x}}_1\\ {9\mathit{x}}_2\\ ⋮\\ 9{\mathit{x}}_{20}\\ 10{\mathit{x}}_{21}\end{array}\right]+\left[\begin{array}{c}{\mathit{x}}_2\\ {\mathit{x}}_3\\ ⋮\\ {\mathit{x}}_{21}\\ 0\end{array}\right]$.

MATLAB® では、これらのベクトルを作成する関数を記述し、それらを合計して、フラグの入力に基づいて A*x または A'*x の値を与えるようにします。

function y = afun(x,flag)
if strcmp(flag,'notransp') % Compute A*x
    y = [0; x(1:20)] ...
        + [(10:-1:0)'; (1:10)'].*x ...
        + 2*[x(2:end); 0];
elseif strcmp(flag,'transp') % Compute A'*x
    y = 2*[0; x(1:20)] ...
        + [(10:-1:0)'; (1:10)'].*x ...
        + [x(2:end); 0];
end
end

(この関数は、ローカル関数として例の最後に保存されています)

ここで、lsqr に A*x および A'*x を計算する関数ハンドルを与えて、線形システム $\mathrm{Ax}=\mathit{b}$ を解きます。1e-6 の許容誤差と 25 回の反復を使用します。$\mathit{A}$ の行の合計として $\mathit{b}$ を指定し、$\mathit{x}$ の真の解が 1 のベクトルとなるようにします。

b = full(sum(A,2));
tol = 1e-6;  
maxit = 25;
x1 = lsqr(@afun,b,tol,maxit)

lsqr converged at iteration 21 to a solution with relative residual 5.4e-13.

x1 = 21×1

    1.0000
    1.0000
    1.0000
    1.0000
    1.0000
    1.0000
    1.0000
    1.0000
    1.0000
    1.0000
      ⋮

ローカル関数

function y = afun(x,flag)
if strcmp(flag,'notransp') % Compute A*x
    y = [0; x(1:20)] ...
        + [(10:-1:0)'; (1:10)'].*x ...
        + 2*[x(2:end); 0];
elseif strcmp(flag,'transp') % Compute A'*x
    y = 2*[0; x(1:20)] ...
        + [(10:-1:0)'; (1:10)'].*x ...
        + [x(2:end); 0];
end
end

入力引数

A — 係数行列

行列 | 関数ハンドル

係数行列。関数ハンドルの行列として指定します。この行列は線形システム A*x = b の係数行列です。一般に、A は大規模なスパース行列、または大規模なスパース行列と列ベクトルの積を返す関数ハンドルです。

関数ハンドルとしての A の指定

オプションで、係数行列を、行列ではなく関数ハンドルとして指定できます。この関数ハンドルは、係数行列全体を作成するのではなく、行列とベクトルの積を返し、計算をより効率的にします。

関数ハンドルを使用するには、関数シグネチャ function y = afun(x,opt) を使用します。関数のパラメーター化では、必要な場合に関数 afun に追加のパラメーターを指定する方法を説明しています。関数 afun は、次の条件を満たさなければなりません。

• afun(x,'notransp') は、A*x の積を返します。

• afun(x,'transp') は、A'*x の積を返します。

許容される関数の例を次に示します。

function y = afun(x,opt,B,C,n)
if strcmp(opt,'notransp')
    y = [B*x(n+1:end); C*x(1:n)];
else
    y = [C'*x(n+1:end); B'*x(1:n)];
end

関数 afun は B および C の値を使用して、実際に行列全体を作成することなく、指定されたフラグに応じて A*x または A'*x を計算します。

データ型: double | function_handle
複素数のサポート: あり

b — 線形方程式の右辺

列ベクトル

線形方程式の右辺。列ベクトルとして指定します。b の長さは size(A,1) と等しくなければなりません。

データ型: double
複素数のサポート: あり

tol — メソッドの許容誤差

[] または 1e-6 (既定値) | 正のスカラー

メソッドの許容誤差。正のスカラーとして指定します。この入力を使用して計算の精度と実行時間とをトレードオフします。成功するには、lsqr は、許容される反復回数内に許容誤差を満たさなければなりません。tol を小さい値にすると、解がより正確でなければ計算が成功しないことを意味します。

データ型: double

maxit — 最大反復回数

[] または min(size(A,1),20) (既定値) | 正のスカラー整数

最大反復回数。正のスカラー整数として指定します。maxit の値を増やして、lsqr が許容誤差 tol を満たすためにより多くの反復を行えるようにします。一般に、tol の値が小さいほど、計算を正常に完了するための反復がより多く必要であるということを意味します。

M, M1, M2 — 前処理行列 (個別の引数として)

eye(size(A)) (既定値) | 行列 | 関数ハンドル

前処理行列。行列または関数ハンドルの個別の引数として指定します。前処理行列 M またはその行列の因子 M = M1*M2 を指定して線形システムの数値的側面を改善し、lsqr での迅速な収束を容易にします。正方係数行列の場合、不完全行列因数分解関数 ilu および ichol を使用して前処理行列を生成できます。また、因数分解の前に equilibrate を使用して、係数行列の条件数を改善できます。前処理行列の詳細については、線形方程式の反復法を参照してください。

lsqr は指定なし前処理行列を単位行列として扱います。

関数ハンドルとしての M の指定

オプションで、M、M1 または M2 のいずれかを、行列ではなく関数ハンドルとして指定できます。関数ハンドルは、前処理行列全体を作成するのではなく行列ベクトル演算を行い、計算をより効率化します。

関数ハンドルを使用するには、まずシグネチャ function y = mfun(x,opt) をもつ関数を作成します。関数のパラメーター化では、必要な場合に関数 mfun に追加のパラメーターを指定する方法を説明しています。関数 mfun は、次の条件を満たさなければなりません。

• mfun(x,'notransp') は M\x または M2\(M1\x) の値を返します。

• mfun(x,'transp') は M'\x または M1'\(M2'\x) の値を返します。

許容される関数の例を次に示します。

function y = mfun(x,opt,a,b)  
if strcmp(opt,'notransp')
    y = x.*a;
else
    y = x.*b;
end
end

この例では、関数 mfun は a および b を使用して、実際に行列 M 全体を作成することなく、指定されたフラグに応じて M\x = x*a または M'\x = x*b を計算します。

データ型: double | function_handle
複素数のサポート: あり

x0 — 初期推定

[] またはゼロの列ベクトル (既定値) | 列ベクトル

初期推定。size(A,2) に等しい長さの列ベクトルとして指定します。lsqr に、既定値のゼロのベクトルではなく、より妥当な初期推定 x0 を与えることができれば、計算時間が節約でき、アルゴリズムがより速く収束するようにできます。

データ型: double
複素数のサポート: あり

出力引数

x — 線形システムの解

列ベクトル

線形システムの解。列ベクトルとして返されます。この出力は線形システム A*x = b の近似解を与えます。

• flag が 0 であり、かつ relres <= tol である場合、x は A*x = b の定数解です。

• flag が 0 であるが relres > tol である場合、x は norm(b-A*x) を最小化する最小二乗解です。この場合、lsvec の出力には x のスケーリングされた正規方程式の誤差が含まれています。

計算が成功しない (flag ~= 0) 場合はいつでも、lsqr によって返される解 x は、すべての反復で計算された最小ノルム残差をもつ解です。

flag — 収束フラグ

スカラー

収束フラグ。次の表のいずれかのスカラー値として返されます。収束フラグは、計算が正常に実行されたかどうかを示し、さまざまな失敗の形式を区別します。

フラグの値	収束
0	成功 — lsqr は希望する許容誤差 tol に反復回数 maxit 以内で収束しました。
1	失敗 — lsqr は maxit 回の反復を行いましたが収束しませんでした。
2	失敗 — 前処理行列 M または M = M1*M2 が悪条件になっています。
3	失敗 — 連続する 2 回の反復が同じであり、lsqr は計算を進めていません。
4	失敗 — lsqr アルゴリズムで計算されたスカラー量の 1 つが、計算を続けるには大きすぎるかまたは小さすぎます。

relres — 相対残差誤差

スカラー

相対残差誤差。スカラーとして返されます。相対残差誤差は、返された答え x がどれだけ正確かを示すものです。lsqr は、求解のプロセスの各反復で相対残差および最小二乗残差を追跡し、"いずれかの" 残差が指定された許容誤差 tol を満たしたときにアルゴリズムは収束します。relres の出力には、収束した残差の値 (相対残差または最小二乗残差) が含まれています。

• 相対残差誤差は norm(b-A*x)/norm(b) に等しく、一般には、lsqr が収束するときの許容誤差 tol を満たす残差です。resvec の出力は、すべての反復にわたってこの残差の履歴を追跡します。

• 最小二乗残差誤差は norm((A*inv(M))'*(B-A*X))/norm(A*inv(M),'fro') に等しくなります。この残差は lsqr が収束する回数が相対残差よりも少なくなる原因となります。lsvec の出力は、すべての反復にわたってこの残差の履歴を追跡します。

iter — 反復回数

スカラー

反復回数。スカラーとして返されます。この出力は、x に対する計算解が計算された時点での反復回数を示します。

データ型: double

resvec — 残差誤差

ベクトル

残差誤差。ベクトルとして返されます。残差誤差 norm(b-A*x) によって、アルゴリズムが x の特定の値に対する収束にどの程度近いかがわかります。resvec の要素数は反復の回数と同じです。resvec の内容を調べて、tol または maxit の値を変更するかどうかを決定することができます。

データ型: double

lsvec — スケーリングされた正規方程式の誤差

ベクトル

スケーリングされた正規方程式の誤差。ベクトルとして返されます。各反復について、lsvec にはスケーリングされた正規方程式の残差 norm((A*inv(M))'*(B-A*X))/norm(A*inv(M),'fro') の推定が含まれています。lsvec の要素数は反復の回数と同じです。

詳細

最小二乗法

最小二乗 (LSQR) アルゴリズムは、方形行列に対する共役勾配 (CG) 法の適応です。解析的には、A*x = b の LSQR は、正規方程式 A'*A*x = A'*b の CG と同じ残差を生じますが、LSQR はより適した数値特性をもち、そのため一般的にはより信頼性があります[1]。

最小二乗法は、方形係数行列および不整合な係数行列を扱うことができる唯一の反復線形システムのソルバーです。

ヒント

• ほとんどの反復メソッドにおける収束は、係数行列の条件数 cond(A) に依存します。A が正方行列の場合、equilibrate を使用して条件数を改善することができ、それ自体でほとんどの反復ソルバーが収束しやすくなります。ただし、equilibrate を使用することでも、平衡化した行列 B = R*P*A*C を次に因子分解する際に前処理行列の品質が向上します。

• dissect や symrcm などの行列の並べ替え関数を使用して係数行列の行と列を並べ替え、係数行列が因子分解されて前処理行列が生成される際に非ゼロの数を最小化できます。これによって、後で前処理を使用した線形システムを解くのに必要なメモリと時間を削減できます。

参照

[1] Barrett, R., M. Berry, T. F. Chan, et al., Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, SIAM, Philadelphia, 1994.

[2] Paige, C. C. and M. A. Saunders, "LSQR: An Algorithm for Sparse Linear Equations And Sparse Least Squares," ACM Trans. Math. Soft., Vol.8, 1982, pp. 43-71.

拡張機能

スレッドベースの環境

MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。

この関数はスレッドベースの環境を完全にサポートしています。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

使用上の注意事項および制限事項:

• b は非スパースの列ベクトルでなければなりません。

• 6 番目の戻り値として最小二乗誤差を出力することはサポートされていません。

詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

分散配列

Parallel Computing Toolbox™ を使用して、クラスターの結合メモリ上で大きなアレイを分割します。

使用上の注意事項および制限事項:

• M1 が関数である場合は、各行に個別に適用されます。

詳細については、分散配列を使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2006a より前に導入

参考

cgs | gmres | minres | norm | pcg | qmr | symmlq

トピック

• 線形方程式の反復法

×

例を開く

この例の変更されたバージョンがあります。編集された方の例を開きますか?

いいえ、変更されたバージョンを上書きします。 はい