スパース行列のグラフィカルな表現

この例では、2 つのトレーリングフラップを含む NASA の翼に対する有限要素メッシュを示します。翼の歴史の詳細情報は、NACA Airfoils (nasa.gov) から入手できます。

データは、ファイル airfoil.mat に格納されています。データは 4253 組のメッシュ点の (x,y) 座標から構成されます。メッシュ点間の結合を指定する 12,289 組のインデックス (i,j) を含む配列も含まれます。

データファイルをワークスペースに読み込みます。

load airfoil

有限要素メッシュの表示

まず、x および y を、範囲が $[0, 1]$ に収まるように $2^{- 32}$ でスケーリングします。次に、(i,j) 結合からスパース隣接行列を作成し、これを正定値にします。最後に、(x,y) を頂点 (メッシュ点) の座標として使用して、隣接行列をプロットします。

% Scaling x and y
x = pow2(x,-32); 
y = pow2(y,-32);

% Forming the sparse adjacency matrix and making it positive definite
n = max(max(i),max(j));
A = sparse(i,j,-1,n,n);
A = A + A';
d = abs(sum(A)) + 1;
A = A + diag(sparse(d));

% Plotting the finite element mesh
gplot(A,[x y])

ans = 86493×1

         0
         0
       NaN
    0.0002
         0
       NaN
         0
    0.0002
       NaN
    0.0002
    0.0002
       NaN
    0.0054
    0.0002
       NaN
      ⋮

title('Airfoil Cross-Section')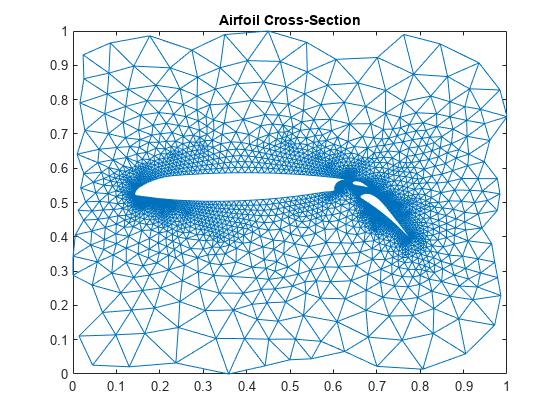

Figure contains an axes object. The axes object with title Airfoil Cross-Section contains an object of type line.

スパースパターンの可視化

spy を使用すると、行列内の非ゼロの要素のパターンを可視化できるため、スパース行列内のスパース性のパターンを確認するには特に便利な関数です。spy(A) は、行列 A のスパース性のパターンをプロットします。

spy(A)
title('Airfoil Adjacency Matrix')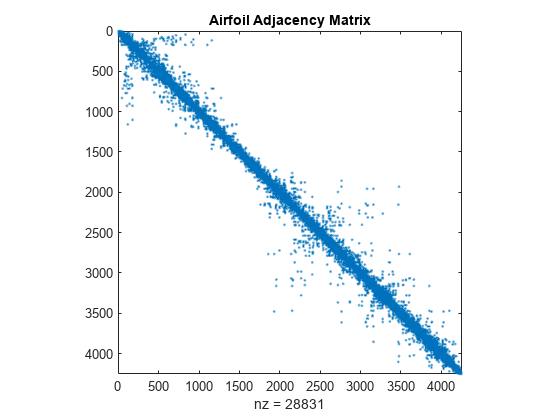

Figure contains an axes object. The axes object with title Airfoil Adjacency Matrix, xlabel nz = 28831 contains a line object which displays its values using only markers.

対称的な並べ替え - 逆 Cuthill-McKee

symrcm は、隣接行列の並べ替えに逆 Cuthill-McKee 手法を使用します。r = symrcm(A) は、A より対角に近い対角要素をもつ傾向がある A(r,r) となるような置換ベクトル r を返します。この形式は、"細長い" 問題から生じる行列の LU 分解またはコレスキー分解に対して、適切な並べ替えを行います。対称と非対称の行列の両方に対して機能します。

r = symrcm(A);
spy(A(r,r))
title('Reverse Cuthill-McKee')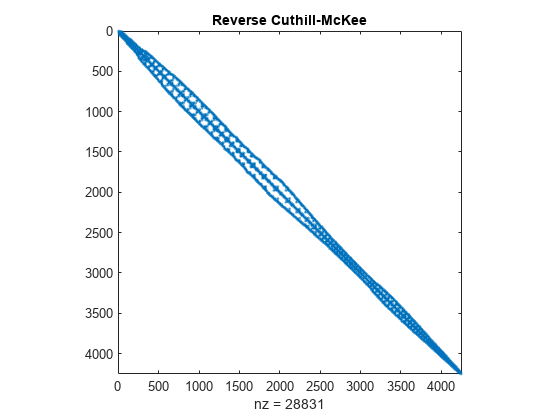

Figure contains an axes object. The axes object with title Reverse Cuthill-McKee, xlabel nz = 28831 contains a line object which displays its values using only markers.

対称的な並べ替え - 列置換

非ゼロ数の非減少のスパース行列で A の列を並べ替えるために、置換ベクトルを返す j = COLPERM(A) を使用します。この形式は、lu(A(:,j)) のような LU 分解の前処理の並べ替えとして有効な場合があります。

j = colperm(A);
spy(A(j,j))
title('Column Count Reordering')

Figure contains an axes object. The axes object with title Column Count Reordering, xlabel nz = 28831 contains a line object which displays its values using only markers.

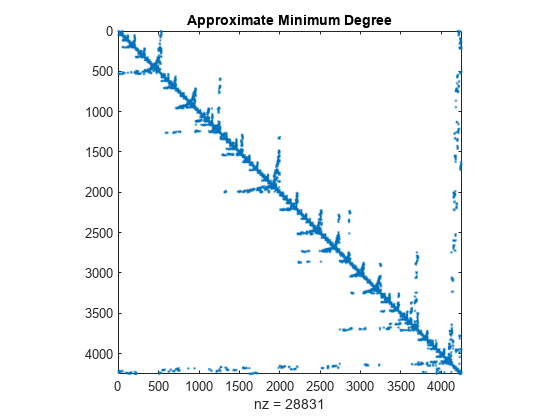
対称的な並べ替え - 対称な近似最小次数

symamd は、対称な近似最小次数置換を与えます。対称正定値行列 A に対して、コマンド p = symamd(S) は S(p,p) が S よりもスパースなコレスキー因子をもつような置換ベクトル p を返します。しばしば、symamd は、対称不定値行列に対しても、問題なく機能します。

m = symamd(A);
spy(A(m,m))
title('Approximate Minimum Degree')

Figure contains an axes object. The axes object with title Approximate Minimum Degree, xlabel nz = 28831 contains a line object which displays its values using only markers.

参考

symamd | symrcm | colperm | spy