tf
伝達関数モデル
説明
tf を使用して、実数値または複素数値の伝達関数モデルを作成するか、または動的システム モデルを伝達関数形式に変換します。
伝達関数は線形時不変システムの周波数領域表現です。たとえば、伝達関数 sys(s) = N(s)/D(s) で表される連続時間 SISO 動的システムについて考えます。ここで、s = jw であり、N(s) と D(s) はそれぞれ分子多項式および分母多項式と呼ばれます。tf モデル オブジェクトは SISO または MIMO 伝達関数を連続時間または離散時間で表現できます。
伝達関数モデル オブジェクトを作成するには、その係数を直接指定するか、あるいは (状態空間モデル ss などの) 別のタイプのモデルを伝達関数形式に変換することができます。詳細については、伝達関数を参照してください。
tf を使用して、一般化状態空間 (genss) モデルや不確かさをもつ状態空間 (uss (Robust Control Toolbox)) モデルを作成することもできます。
作成
構文
説明
伝達関数モデルの作成
sys = tf(numerator,denominator)Numerator プロパティと Denominator プロパティを設定して連続時間の伝達関数モデルを作成します。たとえば、伝達関数 sys(s) = N(s)/D(s) で表される連続時間 SISO 動的システムについて考えます。入力引数の numerator と denominator は、それぞれ N(s) と D(s) の係数です。
sys = tf(numerator,denominator,ts)Numerator、Denominator、Ts の各プロパティを設定して離散時間の伝達関数モデルを作成します。たとえば、伝達関数 sys(z) = N(z)/D(z) で表される離散時間 SISO 動的システムについて考えます。入力引数の numerator と denominator は、それぞれ N(z) と D(z) の係数です。サンプル時間を未指定のままにするには、ts 入力引数を -1 に設定します。
sys = tf(numerator,denominator,ltiSys)ltiSys から継承したプロパティをもつ伝達関数モデルを作成します。
sys = tf(___,PropertyName=Value)
伝達関数モデルへの変換
sys = tf(ltiSys,Name=Value)ltiSys の打ち切られた伝達関数表現を取得します。この手法では、入力と出力の各ペアに対して零点を計算するため、入力と出力のサイズが小さいモデルに最適です。 (R2025a 以降)
入力引数
伝達関数の分子係数。以下として指定します。
多項式係数の行ベクトル。
行ベクトルからなる
Ny行Nu列の cell 配列。これは MIMO 伝達関数を指定し、Nyは出力の数、Nuは入力の数です。
伝達関数を作成するとき、分子係数は降べきの順に指定します。たとえば、伝達関数の分子が 3s^2-4s+5 の場合、numerator は [3 -4 5] として指定します。分子が 2z-1 である離散時間の伝達関数の場合、numerator は [2 -1] に設定します。
tf オブジェクトのプロパティでもあります。詳細については、Numerator を参照してください。
分母係数。以下として指定します。
多項式係数の行ベクトル。
行ベクトルからなる
Ny行Nu列の cell 配列。これは MIMO 伝達関数を指定し、Nyは出力の数、Nuは入力の数です。
伝達関数を作成するとき、分母係数は降べきの順に指定します。たとえば、伝達関数の分母が 7s^2+8s-9 である場合、denominator は [7 8 -9] として指定します。分母が 2z^2+1 である離散時間の伝達関数の場合、denominator は [2 0 1] に設定します。
tf オブジェクトのプロパティでもあります。詳細については、Denominator を参照してください。
スカラーとして指定されたサンプル時間。tf オブジェクトのプロパティでもあります。詳細については、Tsを参照してください。
動的システム。SISO または MIMO 動的システム モデルか、動的システム モデルの配列として指定します。使用できる動的システムには次のようなものがあります。
tfモデル、zpkモデル、ssモデル、pidモデルなどの連続時間または離散時間の数値 LTI モデル。ltiSysがスパース状態空間モデル (sparssまたはmechss) の場合、ソフトウェアは指定された焦点の周波数帯域内における極と零点を計算することで、打ち切られた伝達関数の近似を計算します。スパース モデルの場合は、名前と値の引数を使用して計算オプションを指定します。オプションを指定しなかった場合、ソフトウェアは最小の振幅をもつ最初の 1000 個までの極と零点を計算します。また、この近似の取得は、有効なsparss表現をもつモデルにのみ適用可能です。 (R2025a 以降)genssやuss(Robust Control Toolbox) モデルなどの一般化された、あるいは不確かさをもつ LTI モデル。(不確かさをもつモデルを使用するには Robust Control Toolbox™ ソフトウェアが必要です。)結果の伝達関数は次を仮定します。
調整可能な制御設計ブロックについては調整可能なコンポーネントの現在値。
不確かさをもつ制御設計ブロックについてはモデルのノミナル値。
idtf(System Identification Toolbox)、idss(System Identification Toolbox)、idproc(System Identification Toolbox)、idpoly(System Identification Toolbox)、idgrey(System Identification Toolbox) モデルなどの、同定された LTI モデル。同定されたモデルの変換する成分を選択するには、componentを指定します。componentを指定しない場合、tfは、同定されたモデルの測定成分を既定で変換します。(同定されたモデルを使用するには System Identification Toolbox™ ソフトウェアが必要です。)
静的ゲイン。スカラーまたは行列として指定します。システムの静的ゲインまたは定常状態ゲインは、定常状態の条件下における出力の入力に対する比率を表します。
同定されたモデルの変換対象とするコンポーネント。次のいずれかとして指定します。
'measured'—sysの測定成分を変換します。'noise'—sysのノイズ成分を変換します。'augmented'—sysの測定成分とノイズ成分の両方を変換します。
component が適用されるのは、sys が同定された LTI モデルである場合のみです。
同定された LTI モデルおよびその測定成分とノイズ成分の詳細については、同定された LTI モデルを参照してください。
名前と値の引数
オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。
例: sys = tf(sparseSys,Focus=[0 100],Display="off")
R2025a 以降
零点と極の計算時に並列計算を使用するかどうか。数値または logical 0 (false) または 1 (true) として指定します。
UseParallel が true に設定されている場合、望ましい並列環境に合わせてスケーリングすることを明示的に選択できます。並列計算を有効にすると、零点と極の計算時のパフォーマンスが向上する可能性があります。ただし、UseParallel が false に設定されている場合でも、アルゴリズムは組み込みのマルチスレッディングを使用してローカル リソースを最大限に活用できます。詳細については、MATLAB Multicore を参照してください。
このオプションには、Parallel Computing Toolbox™ ライセンスが必要です。
R2025a 以降
ロールオフの傾き。非正のスカラーまたは行列として指定します。
SISO モデルの場合、または MIMO モデルで入力と出力のすべてのペアに対して傾きが均一な場合には、スカラー値を使用します。
MIMO モデルで入力と出力のペアごとに傾きが異なる場合は、行列を使用します。
このオプションを使用すると、指定された周波数範囲を超えたときに近似がどのようにロールオフする必要があるかを明示的に指定できます。たとえば、Slope を -2 にすると、fmax を超えたときにゲインが少なくとも –40 dB/decade のレート (ロールオフ率 1/s2) でロールオフすることが保証されます。
R2025a 以降
対象の周波数範囲。[0,fmax] の形式のベクトルとして指定します。焦点の周波数範囲を指定すると、ソフトウェアはこの範囲内の固有振動数をもつ極のみを計算します。離散時間モデルの場合、ソフトウェアは双一次変換を使用して同等の固有振動数を近似します。
tf は指定した周波数範囲内のすべての極と零点を計算するため、通常は低周波数範囲を指定して多数の極と零点を計算しないように制限します。既定では、焦点は未指定 ([0 Inf]) であり、アルゴリズムは MaxNumber 個までの極と零点を計算します。
R2025a 以降
計算する極と零点の最大数。正の整数として指定します。この値により、アルゴリズムによって計算される極および零点の数と、元のスパース モデルの近似の次数が制限されます。
R2025a 以降
スペクトル シフト。有限スカラーとして指定します。
ソフトウェアは A-sigma*E に逆べき乗法を使用して、指定した範囲 [0,fmax] 内の固有振動数をもつ極を計算し、シフト sigma に最も近い固有値を取得します。A が特異で、sigma がゼロの場合、逆が存在しないためアルゴリズムは失敗します。したがって、積分動作をもつスパース モデル (s = 0 または z = 1 (離散時間モデルの場合)) では、このオプションを使用して、極または零点をこのシフト値に最も近い値に暗黙的にシフトできます。元のモデルの既存の極または零点の値と等しくないシフト値を指定します。
R2025a 以降
計算された極と零点の精度の許容誤差。正の有限スカラーとして指定します。この値は、逆べき乗法における計算された固有値の収束を制御します。
R2025a 以降
進捗レポートの表示または非表示。"off" または "on" として指定します。
出力引数
出力システム モデル。以下として返されます。
入力引数
numeratorおよびdenominatorが数値配列である場合は、伝達関数 (tf) モデル オブジェクト。ltiSysをtfモデル タイプに変換する場合、sysは常にtfモデル オブジェクトになります。入力引数
numeratorまたはdenominatorにrealpパラメーターまたは一般化行列 (genmat) などの調整可能なパラメーターが含まれる場合は、一般化状態空間モデル (genss) オブジェクト。例については、調整可能なローパス フィルターを参照してください。入力引数
numeratorまたはdenominatorに不確かさをもつパラメーターが含まれる場合は、不確かさをもつ状態空間モデル (uss) オブジェクト。不確かさをもつモデルを使用するには Robust Control Toolbox ソフトウェアが必要です。例については、Transfer Function with Uncertain Coefficients (Robust Control Toolbox)を参照してください。
プロパティ
分子係数。以下として指定します。
降べきの順 (
Variable値's'、'z'、'p'、または'q'の場合) か昇べきの順 (Variable値'z^-1'または'q^-1'の場合) に並べた多項式係数の行ベクトル。行ベクトルからなる
Ny行Nu列の cell 配列。これは MIMO 伝達関数を指定し、Nyは出力の数、Nuは入力の数です。cell 配列の各要素は、与えられた入出力のペアに対し分子係数を指定します。NumeratorとDenominatorの両方を cell 配列として指定する場合、これらの次元は同じでなければなりません。
Numerator の係数は実数値または複素数値にできます。
分母係数。以下として指定します。
降べきの順 (
Variable値's'、'z'、'p'、または'q'の場合) か昇べきの順 (Variable値'z^-1'または'q^-1'の場合) に並べた多項式係数の行ベクトル。行ベクトルからなる
Ny行Nu列の cell 配列。これは MIMO 伝達関数を指定し、Nyは出力の数、Nuは入力の数です。cell 配列の各要素は、与えられた入出力の組み合わせに対し分子係数を指定します。NumeratorとDenominatorの両方を cell 配列として指定する場合、これらの次元は同じでなければなりません。
MIMO 伝達関数のすべての SISO エントリが同じ分母をもつ場合、Denominator を行ベクトル、Numerator を cell 配列として指定することができます。
Denominator の係数は実数値または複素数値にできます。
伝達関数表示変数。以下のいずれかとして指定します。
's'— 連続時間モデルの場合の既定値'z'— 離散時間モデルの既定値'p'—'s'と等価'q'—'z'と等価'z^-1'—'z'の逆'q^-1'—'z^-1'と等価
Variable の値は表示に反映され、また、離散時間モデルの Numerator および Denominator 係数の解釈にも影響を与えます。
Variableの値が's'、'z'、'p'、または'q'の場合、係数は変数の降べきの順に並べられる。たとえば、行ベクトル[ak ... a1 a0]について考えます。多項式の次数は として指定されます。Variableの値が'z^-1'または'q^-1'の場合、係数は変数の昇べきの順に並べられる。たとえば、行ベクトル[b0 b1 ... bk]について考えます。多項式の次数は として指定されます。
例については、離散時間伝達関数における多項式の順序付けの指定、有理式を使用した伝達関数モデル、および有理式を使用した離散時間の伝達関数モデルを参照してください。
伝達遅延。次のいずれかとして指定します。
スカラー — SISO システムに伝達遅延を、または MIMO システムのすべての入出力ペアに対して同じ伝達遅延を指定します。
Ny行Nu列の配列 — MIMO システムの入出力ペアごとに別々の伝達遅延を指定します。ここで、Nyは出力の数、Nuは入力の数です。
連続時間システムの場合は、TimeUnit プロパティによって指定された時間単位で伝達遅延を指定します。離散時間システムの場合、サンプル時間 Ts の整数倍で伝達遅延を指定します。
各入力チャネルの入力遅延。次のいずれかとして指定します。
スカラー — SISO システムに入力遅延を、または多入力システムのすべての入力に同じ遅延を指定します。
Nu行 1 列のベクトル — 多入力システムの入力に別々の入力遅延を指定します。Nuは入力の数です。
連続時間システムの場合は、TimeUnit プロパティによって指定された時間単位で入力遅延を指定します。離散時間システムの場合は、サンプル時間 Ts の整数倍で入力遅延を指定します。
詳細については、線形システムでのむだ時間を参照してください。
各出力チャネルの出力遅延。次のいずれかとして指定します。
スカラー — SISO システムに出力遅延を、または多出力システムのすべての出力に同じ遅延を指定します。
Ny行 1 列のベクトル — 多出力システムの出力に別々の出力遅延を指定します。Nyは出力の数です。
連続時間システムの場合は、TimeUnit プロパティによって指定された時間単位で出力遅延を指定します。離散時間システムの場合は、サンプル時間 Ts の整数倍で出力遅延を指定します。
詳細については、線形システムでのむだ時間を参照してください。
時間変数の単位。次のいずれかとして指定します。
'nanoseconds''microseconds''milliseconds''seconds''minutes''hours''days''weeks''months''years'
TimeUnit の変更は他のプロパティには影響しませんが、システム全体の動作が変わります。chgTimeUnit を使用して、システム動作を変更せずに時間単位を変換します。
入力チャネル名。以下のいずれかとして指定します。
文字ベクトル (単入力モデルの場合)。
文字ベクトルの cell 配列 (多入力モデルの場合)。
''(いずれの入力チャネルにも名前を指定しない場合)。
あるいは、自動的なベクトル拡張を使用して多入力モデルの入力名を割り当てることもできます。たとえば、sys が 2 入力モデルである場合は、以下のように入力します。
sys.InputName = 'controls';入力名は自動的に {'controls(1)';'controls(2)'} へと拡張されます。
省略形表記 u を使用して、InputName プロパティを参照できます。たとえば、sys.u は sys.InputName と同じです。
InputName の使用目的は次のとおりです。
モデル表示とプロット上のチャネルの識別
MIMO システムのサブシステムの抽出
モデル相互接続時における接続点の指定
入力チャネル単位。以下のいずれかとして指定します。
文字ベクトル (単入力モデルの場合)。
文字ベクトルの cell 配列 (多入力モデルの場合)。
''(いずれの入力チャネルにも単位を指定しない場合)。
InputUnit を使用して入力信号の単位を指定します。InputUnit はシステムの動作に影響しません。
入力チャネル グループ。構造体として指定します。InputGroup プロパティを使用して、MIMO システムの入力チャネルをグループに割り当て、各グループを名前で参照します。InputGroup のフィールド名はグループ名であり、フィールドの値は各グループの入力チャネルです。たとえば、入力チャネル 1 と 2、および 3 と 5 をそれぞれ含む、controls および noise という名前の入力グループを作成するには、次のように入力します。
sys.InputGroup.controls = [1 2]; sys.InputGroup.noise = [3 5];
その後、以下を使用して controls 入力からすべての出力にサブシステムを抽出できます。
sys(:,'controls')既定では、InputGroup はフィールドのない構造体です。
出力チャネル名。次のいずれかとして指定されます。
文字ベクトル (単出力モデルの場合)。
文字ベクトルの cell 配列 (多出力モデルの場合)。
''(いずれの出力チャネルにも名前を指定しない場合)。
あるいは、自動的なベクトル拡張を使用して多出力モデルの出力名を割り当てることもできます。たとえば、sys が 2 出力モデルである場合は、以下のように入力します。
sys.OutputName = 'measurements';出力名は自動的に {'measurements(1)';'measurements(2)'} へと拡張されます。
省略形表記 y を使用して OutputName プロパティを参照することもできます。たとえば、sys.y は sys.OutputName と同じです。
OutputName の使用目的は次のとおりです。
モデル表示とプロット上のチャネルの識別
MIMO システムのサブシステムの抽出
モデル相互接続時における接続点の指定
出力チャネル単位。次のいずれかとして指定されます。
文字ベクトル (単出力モデルの場合)。
文字ベクトルの cell 配列 (多出力モデルの場合)。
''(いずれの出力チャネルにも単位を指定しない場合)。
OutputUnit を使用して出力信号の単位を指定します。OutputUnit はシステムの動作に影響しません。
出力チャネル グループ。構造体として指定します。OutputGroup を使用して、MIMO システムの出力チャネルをグループに割り当て、各グループを名前で参照します。OutputGroup のフィールド名はグループ名であり、フィールドの値は各グループの出力チャネルです。たとえば、出力チャネル 1、および 3 と 5 をそれぞれ含む、temperature および measurement という名前の出力グループを作成します。
sys.OutputGroup.temperature = [1]; sys.OutputGroup.measurement = [3 5];
その後、以下を使用してすべての入力から measurement 出力にサブシステムを抽出できます。
sys('measurement',:)既定では、OutputGroup はフィールドのない構造体です。
システム名。文字ベクトルとして指定します。たとえば、'system_1' とします。
システムに関連付けるユーザー指定のテキスト。文字ベクトルまたは文字ベクトルの cell 配列として指定します。たとえば、'System is MIMO' とします。
システムに関連付けるユーザー指定のデータ。任意の MATLAB データ型として指定します。
モデル配列のサンプリング グリッド。構造体配列として指定します。
SamplingGrid を使用して、モデル配列の各モデルに関連付けられている変数値を追跡します。これには同定された線形時不変 (IDLTI) モデル配列も含まれます。
構造体のフィールド名をサンプリング変数の名前に設定します。フィールドの値を、配列内の各モデルに関連付けられているサンプリングされた変数の値に設定します。すべてのサンプリング変数は数値スカラーでなければならず、サンプル値のすべての配列はモデル配列の次元と一致しなければなりません。
たとえば、t = 0:10 の各時点で線形時変システムのスナップショットを記録することにより、線形モデルの 11 行 1 列の配列 sysarr を作成することができます。次のコードは線形モデルでの時間サンプルを格納します。
sysarr.SamplingGrid = struct('time',0:10)同様に、2 つの変数 zeta と w を個別にサンプリングすることにより、6 行 9 列のモデル配列 M を作成できます。次のコードは (zeta,w) の値を M にマッピングします。
[zeta,w] = ndgrid(<6 values of zeta>,<9 values of w>) M.SamplingGrid = struct('zeta',zeta,'w',w)
M を表示する際、配列の各エントリは対応する zeta と w の値を取り込みます。
M
M(:,:,1,1) [zeta=0.3, w=5] =
25
--------------
s^2 + 3 s + 25
M(:,:,2,1) [zeta=0.35, w=5] =
25
----------------
s^2 + 3.5 s + 25
...複数のパラメーター値または操作点で Simulink® モデルを線形化することにより生成されたモデル配列の場合、SamplingGrid には配列の各エントリに対応する変数値が自動的に入力されます。たとえば、Simulink Control Design™ のコマンド linearize (Simulink Control Design) および slLinearizer (Simulink Control Design) により、SamplingGrid が自動的に入力されます。
既定では、SamplingGrid はフィールドのない構造体です。
例
この例では、次の SISO 伝達関数モデルについて考えます。
s の降べきの順に分子係数と分母係数を指定して、伝達関数モデルを作成します。
numerator = 1; denominator = [2,3,4]; sys = tf(numerator,denominator)
sys =
1
---------------
2 s^2 + 3 s + 4
Continuous-time transfer function.
Model Properties
この例では、次の離散時間 SISO 伝達関数モデルについて考えます。
z の降べきの順に分子係数と分母係数を指定し、サンプル時間を 0.1 秒に指定します。離散時間伝達関数モデルを作成します。
numerator = [2,0]; denominator = [4,0,3,-1]; ts = 0.1; sys = tf(numerator,denominator,ts)
sys =
2 z
---------------
4 z^3 + 3 z - 1
Sample time: 0.1 seconds
Discrete-time transfer function.
Model Properties
この例では、既知の固有振動数と減衰比をもつ 2 次システムを表す伝達関数モデルについて考えます。
2 次システムの伝達関数を減衰比 と固有振動数 で表現すると、次のようになります。
減衰比 = 0.25 および固有振動数 = 3 rad/s を仮定して、2 次伝達関数を作成します。
zeta = 0.25; w0 = 3; numerator = w0^2; denominator = [1,2*zeta*w0,w0^2]; sys = tf(numerator,denominator)
sys =
9
---------------
s^2 + 1.5 s + 9
Continuous-time transfer function.
Model Properties
ステップ入力に対するこの伝達関数の応答を調べます。
stepplot(sys)

プロットでは、低減衰比の 2 次システムで予想されるリングダウンが示されています。
離散時間、多入力、多出力のモデルの伝達関数を作成します。
サンプル時間は ts = 0.2 秒です。
分母係数を 2 行 2 列の行列として指定します。
numerators = {1 [1 0];[-1 2] 3};共通分母の係数を行ベクトルとして指定します。
denominator = [1 0.3];
離散時間 MIMO 伝達関数モデルを作成します。
ts = 0.2; sys = tf(numerators,denominator,ts)
sys =
From input 1 to output...
1
1: -------
z + 0.3
-z + 2
2: -------
z + 0.3
From input 2 to output...
z
1: -------
z + 0.3
3
2: -------
z + 0.3
Sample time: 0.2 seconds
Discrete-time transfer function.
Model Properties
MIMO 伝達関数の作成の詳細については、MIMO 伝達関数を参照してください。
この例では、SISO 伝達関数モデルを連結して MIMO 伝達関数モデルを作成します。次の単入力 2 出力の伝達関数について考えます。
SISO 要素を連結して MIMO 伝達関数モデルを指定します。
sys1 = tf([1 -1],[1 1]); sys2 = tf([1 2],[1 4 5]); sys = [sys1;sys2]
sys =
From input to output...
s - 1
1: -----
s + 1
s + 2
2: -------------
s^2 + 4 s + 5
Continuous-time transfer function.
Model Properties
MIMO 伝達関数の作成の詳細については、MIMO 伝達関数を参照してください。
この例では、有理式を使用して連続時間の伝達関数モデルを作成します。有理式を使用すると、分子と分母の多項式係数を指定するよりも簡単でより直観的になる場合があります。
以下のシステムを考えます。
伝達関数モデルを作成するには、まず s を tf オブジェクトとして指定します。
s = tf('s')s = s Continuous-time transfer function. Model Properties
有理式で s を使用して伝達関数モデルを作成します。
sys = s/(s^2 + 2*s + 10)
sys =
s
--------------
s^2 + 2 s + 10
Continuous-time transfer function.
Model Properties
この例では、有理式を使用して離散時間の伝達関数モデルを作成します。有理式を使用すると、多項式係数を指定するよりも簡単でより直観的になる場合があります。
以下のシステムを考えます。
伝達関数モデルを作成するには、まず z を tf オブジェクトとして指定し、サンプル時間 Ts を指定します。
ts = 0.1;
z = tf('z',ts)z = z Sample time: 0.1 seconds Discrete-time transfer function. Model Properties
有理式で z を使用して伝達関数モデルを作成します。
sys = (z - 1) / (z^2 - 1.85*z + 0.9)
sys =
z - 1
------------------
z^2 - 1.85 z + 0.9
Sample time: 0.1 seconds
Discrete-time transfer function.
Model Properties
この例では、別の伝達関数モデルから継承されたプロパティをもつ伝達関数モデルを作成します。次の 2 つの伝達関数について考えます。
この例では、TimeUnit プロパティと InputDelay プロパティを 'minutes' に設定して sys1 を作成します。
numerator1 = [2,0]; denominator1 = [1,8,0]; sys1 = tf(numerator1,denominator1,'TimeUnit','minutes','InputUnit','minutes')
sys1 =
2 s
---------
s^2 + 8 s
Continuous-time transfer function.
Model Properties
propValues1 = [sys1.TimeUnit,sys1.InputUnit]
propValues1 = 1×2 cell
{'minutes'} {'minutes'}
sys1 から継承されたプロパティをもつ 2 つ目の伝達関数モデルを作成します。
numerator2 = [1,-1]; denominator2 = [7,2,0,0,9]; sys2 = tf(numerator2,denominator2,sys1)
sys2 =
s - 1
-----------------
7 s^4 + 2 s^3 + 9
Continuous-time transfer function.
Model Properties
propValues2 = [sys2.TimeUnit,sys2.InputUnit]
propValues2 = 1×2 cell
{'minutes'} {'minutes'}
伝達関数モデル sys2 が sys1 と同じプロパティをもつことを確認してください。
for ループを使用して伝達関数モデルの配列を指定できます。
まず、伝達関数配列にゼロを事前に割り当てます。
sys = tf(zeros(1,1,3));
最初の 2 つのインデックスはモデルの出力と入力の数を表し、3 つ目のインデックスは配列内のモデルの数を表します。
for ループで有理式を使用して伝達関数モデルの配列を作成します。
s = tf('s'); for k = 1:3 sys(:,:,k) = k/(s^2+s+k); end sys
sys(:,:,1,1) =
1
-----------
s^2 + s + 1
sys(:,:,2,1) =
2
-----------
s^2 + s + 2
sys(:,:,3,1) =
3
-----------
s^2 + s + 3
3x1 array of continuous-time transfer functions.
Model Properties
この例では、次の状態空間モデルの伝達関数を計算します。
状態空間行列を使用して状態空間モデルを作成します。
A = [-2 -1;1 -2]; B = [1 1;2 -1]; C = [1 0]; D = [0 1]; ltiSys = ss(A,B,C,D);
状態空間モデル ltiSys を伝達関数に変換します。
sys = tf(ltiSys)
sys =
From input 1 to output:
s
-------------
s^2 + 4 s + 5
From input 2 to output:
s^2 + 5 s + 8
-------------
s^2 + 4 s + 5
Continuous-time transfer function.
Model Properties
この例では、同定された多項式モデルの測定成分とノイズ成分を 2 つの別々の伝達関数に抽出します。
identifiedModel.mat の Box-Jenkins 多項式モデル ltiSys を読み込みます。
load('identifiedModel.mat','ltiSys');
ltiSys は同定された 形式の離散時間モデルで、 は測定成分、 はノイズ成分を表します。
測定成分とノイズ成分を伝達関数として抽出します。
sysMeas = tf(ltiSys,'measured') sysMeas =
From input "u1" to output "y1":
-0.1426 z^-1 + 0.1958 z^-2
z^(-2) * ----------------------------
1 - 1.575 z^-1 + 0.6115 z^-2
Sample time: 0.04 seconds
Discrete-time transfer function.
Model Properties
sysNoise = tf(ltiSys,'noise')sysNoise =
From input "v@y1" to output "y1":
0.04556 + 0.03301 z^-1
----------------------------------------
1 - 1.026 z^-1 + 0.26 z^-2 - 0.1949 z^-3
Input groups:
Name Channels
Noise 1
Sample time: 0.04 seconds
Discrete-time transfer function.
Model Properties
測定成分はプラント モデルとすることができ、ノイズ成分は制御システム設計の外乱モデルとして使用できます。
伝達関数モデル オブジェクトには、モデルが何を表しているかを見失わないために役立つモデル データが含まれています。たとえば、モデルの入力と出力に名前を割り当てることができます。
次の連続時間 MIMO 伝達関数モデルについて考えます。
モデルには 1 つの入力 電流と、2 つの出力 トルクと角速度があります。
まず、モデルの分子係数と分母係数を指定します。
numerators = {[1 1] ; 1};
denominators = {[1 2 2] ; [1 0]};入力名と出力名を指定して、伝達関数モデルを作成します。
sys = tf(numerators,denominators,'InputName','Current',... 'OutputName',{'Torque' 'Angular Velocity'})
sys =
From input "Current" to output...
s + 1
Torque: -------------
s^2 + 2 s + 2
1
Angular Velocity: -
s
Continuous-time transfer function.
Model Properties
この例では、'Variable' プロパティを使用して離散時間伝達関数モデルの多項式の順序付けを指定します。
サンプル時間が 0.1 秒の、次の離散時間伝達関数について考えます。
z 係数を指定して最初の離散時間伝達関数を作成します。
numerator = [1,0,0]; denominator = [1,2,3]; ts = 0.1; sys1 = tf(numerator,denominator,ts)
sys1 =
z^2
-------------
z^2 + 2 z + 3
Sample time: 0.1 seconds
Discrete-time transfer function.
Model Properties
sys1 の係数は z の降べきの順に並べられます。
tf は 'Variable' プロパティの値に基づいて表記を切り替えます。sys2 は sys1 の逆伝達関数モデルであるため、'Variable' を 'z^-1' に指定して同じ分子係数と分母係数を使用します。
sys2 = tf(numerator,denominator,ts,'Variable','z^-1')
sys2 =
1
-------------------
1 + 2 z^-1 + 3 z^-2
Sample time: 0.1 seconds
Discrete-time transfer function.
Model Properties
これで、sys2 の係数は z^-1 の昇べきの順に並べられます。
異なる表記に基づいて、'Variable' プロパティを使用して伝達関数モデルにおける多項式の順序付けを指定できます。
この例では、1 つの調整可能なパラメーター a をもつローパス フィルターを作成します。
tunableTF ブロックの分子と分母の係数が独立しているため、tunableTF を使用して F を表すことはできません。代わりに、調整可能な実数パラメーター オブジェクト realp を使って F を構成します。
初期値 10 の実数の調整可能なパラメーターを作成します。
a = realp('a',10)a =
Name: 'a'
Value: 10
Minimum: -Inf
Maximum: Inf
Free: 1
Real scalar parameter.
調整可能なローパス フィルター F を作成するには、tf を使用します。
numerator = a; denominator = [1,a]; F = tf(numerator,denominator)
Generalized continuous-time state-space model with 1 outputs, 1 inputs, 1 states, and the following blocks: a: Scalar parameter, 2 occurrences. Model Properties Type "ss(F)" to see the current value and "F.Blocks" to interact with the blocks.
F は、Blocks プロパティに調整可能なパラメーター a をもつ genss オブジェクトです。F を他の調整可能なモデルまたは数値モデルと接続して、より複雑な制御システムのモデルを作成できます。例については、調整可能なコンポーネントを含む制御システムを参照してください。
この例では、静的ゲインの MIMO 伝達関数モデルを作成します。
次の 2 入力、2 出力の静的ゲイン行列 m について考えます。
ゲイン行列を指定して静的ゲイン伝達関数モデルを作成します。
m = [2,4;...
3,5];
sys1 = tf(m)sys1 = From input 1 to output... 1: 2 2: 3 From input 2 to output... 1: 4 2: 5 Static gain. Model Properties
上記で取得した静的ゲイン伝達関数モデル sys1 を使用して、別の伝達関数モデルとカスケードさせることができます。
この例では、2 入力 2 出力の離散伝達関数モデルをもう 1 つ作成し、関数 series を使用して 2 つのモデルを接続します。
numerators = {1,[1,0];[-1,2],3};
denominator = [1,0.3];
ts = 0.2;
sys2 = tf(numerators,denominator,ts)sys2 =
From input 1 to output...
1
1: -------
z + 0.3
-z + 2
2: -------
z + 0.3
From input 2 to output...
z
1: -------
z + 0.3
3
2: -------
z + 0.3
Sample time: 0.2 seconds
Discrete-time transfer function.
Model Properties
sys = series(sys1,sys2)
sys =
From input 1 to output...
3 z^2 + 2.9 z + 0.6
1: -------------------
z^2 + 0.6 z + 0.09
-2 z^2 + 12.4 z + 3.9
2: ---------------------
z^2 + 0.6 z + 0.09
From input 2 to output...
5 z^2 + 5.5 z + 1.2
1: -------------------
z^2 + 0.6 z + 0.09
-4 z^2 + 21.8 z + 6.9
2: ---------------------
z^2 + 0.6 z + 0.09
Sample time: 0.2 seconds
Discrete-time transfer function.
Model Properties
R2025a 以降
この例では、スパース状態空間モデルの打ち切られた伝達関数モデルを取得する方法を示します。この例では、円柱ロッドの熱分布の熱モデルを線形化することで得られるスパース モデルを使用します。
モデル データを読み込みます。
load cylindricalRod.mat
sys = sparss(A,B,C,D,E);
w = logspace(-7,-1,20);
size(sys)Sparse state-space model with 3 outputs, 1 inputs, and 7522 states.
モデルの周波数応答を解析します。
sigmaplot(sys,w)
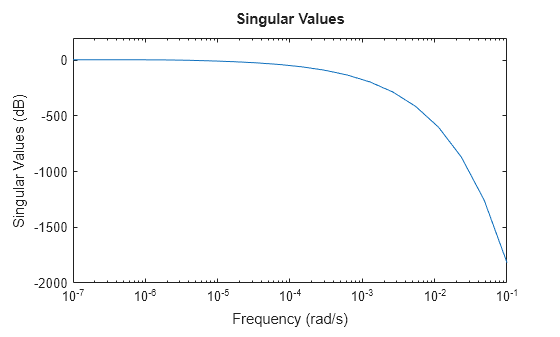
打ち切られた近似を得るには、tf を使用して、焦点の周波数帯域を指定します。このモデルでは、0 rad/s ~ 0.01 rad/s までの周波数範囲を使用することで、低次の近似が得られます。
tsys = tf(sys,Focus=[0 1e-2],Display="off");周波数応答を比較します。
sigmaplot(sys,tsys,w)
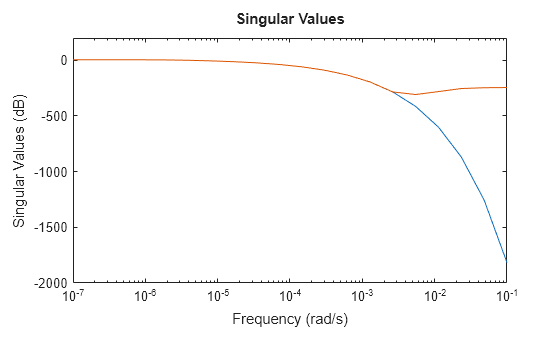
この熱モデルでは、0.001 rad/s を超えると急勾配のロールオフが生じています。既定では、tf を使用して得られた低次元化モデルは、このロールオフに適切に一致しません。これを軽減するために、tf の RollOff 引数を使用して、焦点の周波数帯域を超えたときの最小ロールオフ値を指定できます。ロールオフの傾きの値として -45 を指定します。これは、–900 db/decade 以上のレートに相当します。
tsys2 = tf(sys,Focus=[0 1e-2],RollOff=-45,Display="off");
sigmaplot(sys,tsys2,w)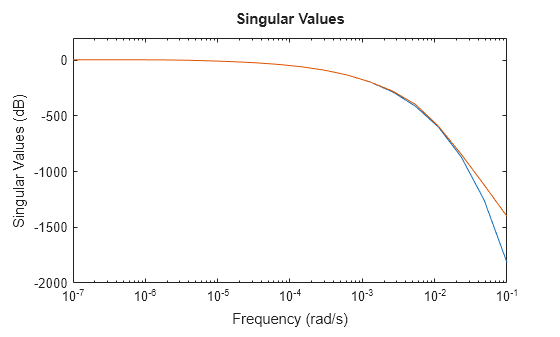
低次元化されたモデルで、ロールオフ値の近似が大幅に改善されました。ただし、この例では、tf を使用してロールオフの傾きを再調整するには、零点と極を再計算する必要があります。そのため、大規模モデルの場合、計算コストが高くなる可能性があります。代わりに、reducespecの零点-極打ち切り法を使用して、ソフトウェアが極と零点を計算した後に、追加の計算コストをかけずにロールオフを調整できます。例については、Zero-Pole Truncation of Thermal Modelを参照してください。
制限
伝達関数モデルは、数値計算に適していません。作成後は他のモデルとの組み合わせやモデルの変換を行う前に、状態空間形式に変換してください。その後、結果のモデルを検査目的で伝達関数形式に変換し直すことができます。
同定された非線形モデルは
tfを使用して伝達関数モデルに直接変換できません。伝達関数モデルを取得するには、次を行います。linapp(System Identification Toolbox)、idnlarx/linearize(System Identification Toolbox)、またはidnlhw/linearize(System Identification Toolbox) を使用して、同定された非線形モデルを同定された LTI モデルに変換します。次に、結果のモデルを
tfを使用して伝達関数モデルに変換します。
アルゴリズム
スパース モデルを変換するために、tf は逆べき乗法に Krylov-Schur アルゴリズム [1] を使用して、指定した周波数帯域内の極と零点を計算します。
参照
[1] Stewart, G. W. “A Krylov--Schur Algorithm for Large Eigenproblems.” SIAM Journal on Matrix Analysis and Applications 23, no. 3 (January 2002): 601–14. https://doi.org/10.1137/S0895479800371529.
バージョン履歴
R2006a より前に導入tf を使用してスパース状態空間モデルを変換し、打ち切られた伝達関数の近似を取得できるようになりました。tf は、(通常は特定の低周波数帯域 [0 fmax] で) スパース モデルの零点と極のサブセットを計算します。これにより、計算量が増加する代わりに、モーダル打ち切りによるモデル次数の低次元化よりも優れた低周波数の近似が得られます。また、tf では、周波数 fmax を超えたときのロールオフの傾きを直接制御することもできます。新しい構文 tsys = tf(sparseSys,Name=Value) を使用して、焦点の周波数範囲などの指定したオプションに基づいて近似を得ます。例については、スパース モデルの打ち切られた伝達関数の近似の計算を参照してください。
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Web サイトの選択
Web サイトを選択すると、翻訳されたコンテンツにアクセスし、地域のイベントやサービスを確認できます。現在の位置情報に基づき、次のサイトの選択を推奨します:
また、以下のリストから Web サイトを選択することもできます。
最適なサイトパフォーマンスの取得方法
中国のサイト (中国語または英語) を選択することで、最適なサイトパフォーマンスが得られます。その他の国の MathWorks のサイトは、お客様の地域からのアクセスが最適化されていません。
南北アメリカ
- América Latina (Español)
- Canada (English)
- United States (English)
ヨーロッパ
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)