genss

一般化状態空間モデル

説明

一般化状態空間 (genss) モデルは、調整可能なパラメーターまたはコンポーネントを含む状態空間モデルです。genss モデルは、数値 LTI モデルを調整可能なコンポーネント (制御設計ブロック) を含むモデルと組み合わせたときに発生します。数値 LTI モデルと制御設計ブロックの詳細については、調整可能な係数をもつモデルを参照してください。

一般化状態空間モデルを使用すると、固定および調整可能なコンポーネントが混在している制御システムを表すことができます。一般化状態空間モデルは、systune や looptune といったコマンドを使用したパラメーター調査やパラメーター調整などの制御設計作業に使用します。

作成

genss モデルを構築するには、次を行います。

series、parallel、lft、または connect か、算術演算子 +、-、*、/、\、および ^ を使用して数値 LTI モデルと制御設計ブロックを組み合わせる。
tf または ss で、数値または数値配列ではなく調整可能なパラメーター (realp) または一般化行列 (genmat) である 1 つ以上の入力引数を使用する。
genss コマンドを使用して任意の数値 LTI モデルまたは制御設計ブロックを変換する。たとえば、次のコードは sys を genss モデル gensys に変換します。
```
gensys = genss(sys)
```
frd モデルと genfrd モデルについては、genss を使用した変換はサポートされていません。
getIOTransfer (Simulink Control Design) や getLoopTransfer (Simulink Control Design) のようなコマンドを使用して、slTuner (Simulink Control Design) インターフェイスから genss モデルを抽出する。抽出した genss モデルには、インターフェイスで指定されたすべての調整可能なブロックおよび解析ポイントが含まれます。

プロパティ

すべて展開する

`Blocks` — 制御設計ブロック
構造体

一般化 LTI モデルまたは一般化行列に含まれる制御設計ブロック。構造体として指定します。Blocks のフィールド名は、制御設計ブロックの Name プロパティです。

ドット表記を使用すると、これらの制御設計ブロックのいくつかの属性を変更できます。たとえば、一般化 LTI モデルまたは一般化行列 M が realp の調整可能なパラメーター a を含んでいる場合に a の現在の値を変更します。

M.Blocks.a.Value = -1;

`A,B,C,D` — 調整可能なパラメーターおよび不確かさをもつパラメーターに対する状態空間行列の依存関係
`genmat` オブジェクト | `umat` オブジェクト | double の配列

調整可能なパラメーターおよび不確かさをもつパラメーターに対する状態空間行列の依存関係。一般化行列 (genmat)、不確かさをもつ行列 (umat)、または double 配列として格納されます。

これらのプロパティは、静的な制御設計ブロック realp、ureal、ucomplex、または ucomplexm に対する状態空間行列の依存関係をモデル化します。tunableGain や tunableSS などの動的な制御設計ブロックはそれらの現在の値に設定され、内部遅延はゼロに設定されます。

対応する状態空間行列が静的な制御設計ブロックに一切依存しない場合、これらのプロパティは double 行列となります。

例については、状態空間行列のパラメーターへの依存関係を参照してください。

`E` — E 行列
double の行列

E 行列。一般化状態空間方程式が陰的である場合、double 行列として格納されます。値 E = [] は、一般化状態空間方程式が陽的であることを意味します。陰的な状態空間モデルの詳細については、状態空間モデルを参照してください。

`StateName` — 状態名
各状態に対して `''` (既定値) | 文字ベクトル | 文字ベクトルの cell 配列

状態名。次のいずれかとして格納されます。

文字ベクトル — 'velocity' などの 1 次モデルの場合。
文字ベクトルの cell 配列 — 2 つ以上の状態をもつモデルの場合 (たとえば {'position';'velocity'} など)。
'' — 名前のない状態の場合。

genss モデルに状態名を割り当てることができるのは、そのすべての制御設計ブロックが静的な場合のみです。それ以外の場合、コンポーネントモデルに状態名を指定した後で、コンポーネントモデルを相互接続して genss モデルを作成します。これを行うと、genss モデルは割り当てられた状態名を追跡します。例については、一般化状態空間モデルの状態名の追跡を参照してください。

`StateUnit` — 状態単位のラベル
文字ベクトル | 文字ベクトルの cell 配列 | `''`

状態単位のラベル。次のいずれかとして格納されます。

文字ベクトル — 'm/s' などの 1 次モデルの場合。
文字ベクトルの cell 配列 — 2 つ以上の状態をもつモデルの場合 (たとえば {'m';'m/s'} など)。
'' — 名前のない状態の場合。

StateUnit は便宜上、各状態の単位にラベルを付けますが、システムの動作には影響しません。

genss モデルに状態単位を割り当てることができるのは、そのすべての制御設計ブロックが静的な場合のみです。それ以外の場合、コンポーネントモデルに状態単位を指定した後で、コンポーネントモデルを相互接続して genss モデルを作成します。これを行うと、genss モデルは割り当てられた状態単位を追跡します。例については、一般化状態空間モデルの状態名の追跡を参照してください。

`InternalDelay` — 内部遅延
スカラー | ベクトル

内部遅延。スカラーまたはベクトルとして指定します。内部遅延は、たとえば、システムで遅延のあるフィードバックループを閉じるときや、遅延システムを順番にまたは並列で接続するときに生じます。内部遅延の詳細については、むだ時間のある閉フィードバックループを参照してください。

連続時間モデルの場合、内部遅延はモデルの TimeUnit プロパティで指定された時間単位で表現されます。

離散時間モデルの場合、内部遅延はサンプル時間 Ts の整数倍として表現されます。たとえば、InternalDelay = 3 は 3 サンプリング周期の遅延を意味します。

`InputDelay` — 入力遅延
すべての出力チャネルに対して `0` | スカラー | ベクトル

入力遅延。スカラーまたは入力の数と等しい長さのベクトルとして指定します。

N_u 個の入力があるシステムの場合、InputDelay を N_u 行 1 列のベクトルに設定します。ここで、それぞれのエントリは、対応する入力チャネル用の入力遅延を表す数値です。すべての入力チャネルに同じ遅延を適用するには、InputDelay をスカラー値として指定します。

連続時間システムの場合、TimeUnit プロパティに格納された時間単位で入力遅延を指定します。

離散時間システムの場合、サンプル時間 Ts の整数倍で入力遅延を指定します。たとえば、InputDelay = 3 は 3 サンプリング周期の遅延を意味します。

`OutputDelay` — 出力遅延
すべての出力チャネルに対して `0` | スカラー | ベクトル

出力遅延。スカラーまたは出力の数と等しい長さのベクトルとして指定します。

N_y 個の出力があるシステムの場合、OutputDelay を N_y 行 1 列のベクトルに設定します。ここで、それぞれのエントリは、対応する出力チャネル用の出力遅延を表す数値です。すべての出力チャネルに同じ遅延を適用するには、OutputDelay をスカラー値として指定します。

連続時間システムの場合、TimeUnit プロパティに格納された時間単位で出力遅延を指定します。

離散時間システムの場合、サンプル時間 Ts の整数倍で出力遅延を指定します。たとえば、OutputDelay = 3 は 3 サンプリング周期の遅延を意味します。

`Ts` — サンプル時間
`0` (連続時間) (既定値) | `-1` (離散時間) | スカラー

サンプル時間。連続時間モデルの場合、Ts = 0。離散時間モデルの場合、Ts はサンプリング周期を表す正のスカラーです。この値は、モデルの TimeUnit プロパティで指定される単位で表されます。指定のないサンプル時間を伴う離散時間モデルを示すには、Ts = -1 と設定します。

このプロパティを変更してもモデルの離散化やリサンプリングは行われません。

`TimeUnit` — 時間変数の単位
`'seconds'` (既定値)

モデル内の時間変数、サンプル時間 Ts および何らかのむだ時間の単位。以下のいずれかの値として指定します。

'nanoseconds'
'microseconds'
'milliseconds'
'seconds'
'minutes'
'hours'
'days'
'weeks'
'months'
'years'

このプロパティを変更しても他のプロパティには影響しないため、システム全体の動作が変更されます。chgTimeUnit を使用して、システム動作を変更せずに時間単位を変換します。

`InputName` — 入力チャネル名
文字ベクトル | 文字ベクトルの cell 配列

入力チャネル名。以下のいずれかとして指定します。

文字ベクトル — 単入力モデルの場合 (たとえば 'controls' など)。
文字ベクトルの cell 配列 — 多入力モデルの場合。

または、自動的なベクトル拡張を使用して多入力モデルの入力名を割り当てます。たとえば、sys が 2 入力モデルである場合は、以下のようになります。

sys.InputName = 'controls';

入力名は自動的に {'controls(1)';'controls(2)'} へと拡張されます。

省略形表記 u を使用して、InputName プロパティを参照できます。たとえば、sys.u は sys.InputName と同じです。

以下を含めて、入力チャネル名はいくつかの用途をもちます。

モデル表示とプロット上のチャネルの識別
MIMO システムのサブシステムの抽出
モデル相互接続時における接続点の指定

`InputUnit` — 入力チャネル単位
文字ベクトル | 文字ベクトルの cell 配列

入力チャネル単位。以下のいずれかとして指定します。

文字ベクトル — 単入力モデルの場合 (たとえば 'seconds' など)。
文字ベクトルの cell 配列 — 多入力モデルの場合。

InputUnit を使用して入力信号単位を追跡します。InputUnit はシステムの動作に影響しません。

`InputGroup` — 入力チャネルグループ
構造体

MIMO システムの入力チャネルを割り当てるための入力チャネルグループ。構造体として指定します。この構造体においてフィールド名はグループ名であり、フィールド値は各グループに属する入力チャネルです。以下に例を示します。

sys.InputGroup.controls = [1 2];
sys.InputGroup.noise = [3 5];

これは、入力チャネル 1、2 および 3、5 をそれぞれ含む controls および noise という名前の入力グループを作成します。その後、以下を使用して controls 入力からすべての出力にサブシステムを抽出できます。

sys(:,'controls')

`OutputName` — 出力チャネル名
文字ベクトル | 文字ベクトルの cell 配列

出力チャネル名。次のいずれかとして指定されます。

文字ベクトル — 単出力モデルの場合。たとえば、'measurements' とします。
文字ベクトルの cell 配列 — 多出力モデルの場合。

または、自動的なベクトル拡張を使用して多出力モデルの出力名を割り当てます。たとえば、sys が 2 出力力モデルである場合は、以下のようになります。

sys.OutputName = 'measurements';

出力名は自動的に {'measurements(1)';'measurements(2)'} へと拡張されます。

省略形表記 y を使用して、OutputName プロパティを参照できます。たとえば、sys.y は sys.OutputName と同じです。

以下を含めて、出力チャネル名はいくつかの用途をもちます。

モデル表示とプロット上のチャネルの識別
MIMO システムのサブシステムの抽出
モデル相互接続時における接続点の指定

`OutputUnit` — 出力チャネル単位
文字ベクトル | 文字ベクトルの cell 配列

出力チャネル単位。次のいずれかとして指定されます。

文字ベクトル — 単出力モデルの場合。たとえば、'seconds' とします。
文字ベクトルの cell 配列 — 多出力モデルの場合。

OutputUnit を使用して出力信号単位を追跡します。OutputUnit はシステムの動作に影響しません。

`OutputGroup` — 出力チャネルグループ
`struct` (既定値)

MIMO システムの出力チャネルを割り当てるための出力チャネルグループ。構造体として指定します。この構造体内においてフィールド名はグループ名であり、フィールド値は各グループに属する出力チャネルです。以下に例を示します。

sys.OutputGroup.temperature = [1];
sys.OutputGroup.measurement = [3 5];

これは、出力チャネル 1 および 3、5 をそれぞれ含む temperature および measurement という名前の出力グループを作成します。その後、以下を使用してすべての入力から measurement 出力にサブシステムを抽出できます。

sys('measurement',:)

`Name` — システム名
文字ベクトル

システム名。文字ベクトルとして指定します。たとえば、'system_1' とします。

`Notes` — システムに関連付ける任意のテキスト
string | 文字ベクトルの cell 配列

システムに関連付ける任意のテキスト。string または文字ベクトルの cell 配列として格納されます。プロパティには指定したデータ型が格納されます。たとえば、sys1 と sys2 が動的システムモデルである場合、その Notes プロパティを次のように設定できます。

sys1.Notes = "sys1 has a string.";
sys2.Notes = 'sys2 has a character vector.';
sys1.Notes
sys2.Notes

ans = 

    "sys1 has a string."


ans =

    'sys2 has a character vector.'

`UserData` — システムに関連付ける任意のデータ型
任意の MATLAB^® データ

システムに関連付ける任意のデータ型。任意の MATLAB データ型として指定します。

`SamplingGrid` — モデル配列のサンプリンググリッド
`[]` (既定値) | 構造体

モデル配列のサンプリンググリッド。構造体として指定します。

1 つ以上の独立変数をサンプリングすることによって得られるモデル配列の場合、このプロパティは配列内の各モデルに関連付けられた変数値を追跡します。この情報はモデル配列を表示またはプロットすると表示されます。この情報を使用して、結果を独立変数まで遡ります。

データ構造のフィールド名をサンプリング変数の名前に設定します。フィールドの値を、配列内の各モデルに関連付けられているサンプリングされた変数の値に設定します。すべてのサンプリング変数は数値でスカラー値でなければならず、サンプル値のすべての配列はモデル配列の次元に一致しなければなりません。

たとえば、t = 0:10 の各時点で線形時変システムのスナップショットを記録することにより、線形モデルの 11 行 1 列の配列 sysarr を作成するとします。次のコードは線形モデルでの時間サンプルを格納します。

 sysarr.SamplingGrid = struct('time',0:10)

同様に、2 つの変数 zeta と w を個別にサンプリングすることにより、6 行 9 列のモデル配列 M を作成するとします。次のコードは (zeta,w) の値を M に付加します。

[zeta,w] = ndgrid(<6 values of zeta>,<9 values of w>)
M.SamplingGrid = struct('zeta',zeta,'w',w)

M を表示する際、配列の各エントリは対応する zeta と w の値を取り込みます。

M(:,:,1,1) [zeta=0.3, w=5] =
 
        25
  --------------
  s^2 + 3 s + 25
 

M(:,:,2,1) [zeta=0.35, w=5] =
 
         25
  ----------------
  s^2 + 3.5 s + 25
 
...

複数のパラメーター値または操作点で Simulink^® モデルを線形化することにより生成されたモデル配列の場合、SamplingGrid には配列の各エントリに対応する変数値が自動的に入力されます。たとえば、Simulink Control Design™ のコマンドである linearize (Simulink Control Design) や slLinearizer (Simulink Control Design) は、この方法で SamplingGrid に入力します。

オブジェクト関数

以下のリストには、genss モデルで使用できる関数の代表的なサブセットが含まれています。一般に、数値 LTI モデルに適用できる関数の多くは genss モデルにも適用できます。

すべて展開する

応答の抽出

`getIOTransfer`	制御システムの一般化モデルからの閉ループ伝達関数
`getLoopTransfer`	`genss` モデルで表される制御システムの開ループ伝達関数
`getSensitivity`	制御システムの一般化モデルからの感度関数
`getCompSensitivity`	制御システムの一般化モデルからの相補感度関数

ブロックおよび値へのアクセス

`getValue`	一般化モデルの現在値
`getBlockValue`	一般化モデルの制御設計ブロックの現在値を取得
`setBlockValue`	一般化モデルの制御設計ブロックの値の変更

線形解析

`bode`	動的システムのボード周波数応答
`sigma`	動的システムの周波数応答の特異値
`nyquist`	動的システムのナイキスト応答
`step`	動的システムのステップ応答
`lsim`	任意の入力に対する動的システムの時間応答シミュレーションデータを計算
`margin`	ゲイン余裕、位相余裕、および交差周波数

モデルの相互接続

`feedback`	複数のモデルのフィードバック接続
`connect`	動的システムのブロック線図相互接続
`series`	2 つのモデルの直列接続
`parallel`	2 つのモデルの並列接続

コントローラーの調整

`systune`	MATLAB でモデル化された固定構造制御システムの調整
`looptune`	固定構造フィードバックループの調整

例

すべて折りたたむ

調整可能なローパスフィルター

ライブスクリプトを開く

この例では、1 つの調整可能なパラメーター a をもつローパスフィルターを作成します。

$F = \frac{a}{s + a}$

tunableTF ブロックの分子と分母の係数が独立しているため、tunableTF を使用して F を表すことはできません。代わりに、調整可能な実数パラメーターオブジェクト realp を使って F を構成します。

初期値 10 の実数の調整可能なパラメーターを作成します。

a = realp('a',10)

a = 
       Name: 'a'
      Value: 10
    Minimum: -Inf
    Maximum: Inf
       Free: 1

Real scalar parameter.

調整可能なローパスフィルター F を作成するには、tf を使用します。

numerator = a;
denominator = [1,a];
F = tf(numerator,denominator)

Generalized continuous-time state-space model with 1 outputs, 1 inputs, 1 states, and the following blocks:
  a: Scalar parameter, 2 occurrences.
Model Properties

Type "ss(F)" to see the current value and "F.Blocks" to interact with the blocks.

F は、Blocks プロパティに調整可能なパラメーター a をもつ genss オブジェクトです。F を他の調整可能なモデルまたは数値モデルと接続して、より複雑な制御システムのモデルを作成できます。例については、調整可能なコンポーネントを含む制御システムを参照してください。

固定パラメーターと調整可能なパラメーターの両方をもつ状態空間モデルの作成

ライブスクリプトを開く

この例では、固定パラメーターと調整可能なパラメーターの両方をもつ状態空間genssモデルを作成する方法を説明します。

$A = [\begin{array}{cccccccccccccccccccc} 1 & a + b \\ 0 & a b \end{array}], B = [\begin{array}{cccccccccccccccccccc} - 3.0 \\ 1.5 \end{array}], C = [\begin{array}{cccccccccccccccccccc} 0.3 & 0 \end{array}], D = 0,$

ここで、a と b は初期値がそれぞれ -1 と 3 の調整可能なパラメーターです。

realpを使用して調整可能なパラメーターを作成します。

a = realp('a',-1);
b = realp('b',3);

a と b の代数式を使って一般化行列を定義します。

A = [1 a+b;0 a*b];

A は、Blocks プロパティに a と b を含む一般化行列です。a と b の初期値から、A の初期値は [1 2;0 -3] です。

固定値状態空間行列を作成します。

B = [-3.0;1.5];
C = [0.3 0];
D = 0;

ssを使用して状態空間モデルを作成します。

sys = ss(A,B,C,D)

Generalized continuous-time state-space model with 1 outputs, 1 inputs, 2 states, and the following blocks:
  a: Scalar parameter, 2 occurrences.
  b: Scalar parameter, 2 occurrences.
Model Properties

Type "ss(sys)" to see the current value and "sys.Blocks" to interact with the blocks.

sys は、調整可能なパラメーター a および b を含む一般化 LTI モデル (genss) です。

数値および調整可能なコンポーネントの両方をもつ制御システムモデル

ライブスクリプトを開く

この例では、固定されたプラントとセンサーダイナミクスおよび調整可能な制御コンポーネントの両方をもつ制御システムの調整可能モデルを作成する方法を示します。

次の図の制御システムについて考えます。

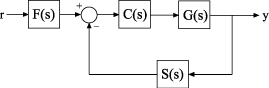
プラント応答は $G (s) = 1 / (s + 1)^{2}$ で、センサーダイナミクスのモデルは $S (s) = 5 / (s + 4)$ であると仮定します。コントローラー $C$ は調整可能な PID コントローラーであり、プレフィルター $F = a / (s + a)$ は 1 つの調整可能なパラメーター a をもつローパスフィルターです。

プラントとセンサーダイナミクスを表すモデルを作成します。プラントとセンサーダイナミクスは固定なので、それらを数値 LTI モデルで表します。

G = zpk([],[-1,-1],1);
S = tf(5,[1 4]);

調整可能なコンポーネントをモデル化するには、制御設計ブロックを使用します。コントローラー C の調整可能な表現を作成します。

C = tunablePID('C','PID');

C は tunablePID オブジェクトであり、事前定義された比例-積分-微分 (PID) 構造をもつ制御設計ブロックです。

1 つの調整可能なパラメーターをもつフィルター $F = a / (s + a)$ のモデルを作成します。

a = realp('a',10); 
F = tf(a,[1 a]);

a は、初期値 10 の realp (調整可能な実数パラメーター) オブジェクトです。a を tf 内の係数として使用すると、調整可能な genss モデルオブジェクト F が作成されます。

モデルを相互接続して r から y への完全な閉ループ応答のモデルを作成します。

T = feedback(G*C,S)*F

Generalized continuous-time state-space model with 1 outputs, 1 inputs, 5 states, and the following blocks:
  C: Tunable PID controller, 1 occurrences.
  a: Scalar parameter, 2 occurrences.
Model Properties

Type "ss(T)" to see the current value and "T.Blocks" to interact with the blocks.

T は genss モデルオブジェクトです。数値 LTI モデルのみを接続することによって形成される統合モデルとは対照的に、T は制御システムの調整可能な要素を記録しています。調整可能な要素は、genss モデルオブジェクトの Blocks プロパティに格納されます。T の調整可能な要素を調べます。

T.Blocks

ans = struct with fields:
    C: [1×1 tunablePID]
    a: [1×1 realp]

調整可能なコンポーネントをもつ制御システムの genss モデルを作成する場合は、systune などの調整コマンドを使用して、指定した設計要件を満たすように自由パラメーターを調整できます。

一般化状態空間モデルの状態名の追跡

ライブスクリプトを開く

ラベル付きの状態名をもつ genss モデルを作成します。これを行うには、コンポーネントモデルを相互接続する前に、コンポーネントの LTI モデルの状態にラベルを付けます。たとえば、2 状態の固定係数プラントモデルと 1 状態の調整可能なコントローラーを接続します。

A = [-1 -1; 1 0];
B = [1; 0];
C = [0 1];
D = 0;
G = ss(A,B,C,D);
G.StateName = {'Pstate1','Pstate2'};

C = tunableSS('C',1,1,1);

L = G*C;

genss モデル L は、これを作成したコンポーネントの状態名を保持します。調整可能なコンポーネント C には状態名を割り当てていないため、ソフトウェアが自動的に状態名を割り当てます。確認するには、L の状態名を調べます。

L.StateName

ans = 3×1 cell
    {'Pstate1'}
    {'Pstate2'}
    {'C.x1'   }

制御設計ブロックに状態名が自動的に割り当てられることで、一般化モデルのどの状態が調整可能コンポーネントから得られたものかを追跡することができます。

状態名は、genss モデルを固定係数の状態空間モデルに変換する場合にも保持されます。確認するには、L を ss 形式に変換します。

Lfixed = ss(L);
Lfixed.StateName

ans = 3×1 cell
    {'Pstate1'}
    {'Pstate2'}
    {'C.x1'   }

genss モデルの StateUnit プロパティに格納される状態単位ラベルも同様に動作します。

状態空間行列のパラメーターへの依存関係

ライブスクリプトを開く

調整可能なパラメーターをもつ一般化モデルを作成し、そのパラメーターに対する行列 A の依存関係を調べます。これを行うには、一般化モデルの A プロパティを調べます。

G = tf(1,[1 10]);
k = realp('k',1);
F = tf(k,[1 k]);
L1 = G*F;
L1.A

Generalized matrix with 2 rows, 2 columns, and the following blocks:
  k: Scalar parameter, 2 occurrences.
Model Properties

Type "double(ans)" to see the current value and "ans.Blocks" to interact with the blocks.

A プロパティは、調整可能な実数パラメーター k への依存関係を保持する一般化行列です。状態空間行列のプロパティ A、B、C、および D は、静的パラメーターへの依存関係のみを保持します。genss モデルが動的な制御設計ブロックをもつ場合、状態空間行列のプロパティを評価に際して、これらはその現在値に設定されます。たとえば、調整可能な PI ブロックをもつ genss モデルの行列 A のプロパティを調べます。

C = tunablePID('C','PI');
L2 = G*C;
L2.A

ans = 2×2

  -10.0000    0.0010
         0         0

ここで、行列 A は double 行列として格納され、その値は L2 の現在の値からなる行列 A です。

L2cur = ss(L2);
L2cur.A

ans = 2×2

  -10.0000    0.0010
         0         0

また、ssdata を使用して状態空間行列を抽出すると、静的ブロックも含め、すべての制御設計ブロックがその現在の値またはノミナル値に設定されます。したがって、以下の操作はすべて L1 の行列 A の現在の値を返します。

[A,B,C,D] = ssdata(L1);
A

double(L1.A)

L1cur = ss(L1);
L1cur.A

ヒント

genss モデルは通常の ss モデルとして扱うことができます。bode や step などの解析コマンドは、調整可能な各パラメーターをその現在の値に置き換えることによってモデルを評価します。

バージョン履歴

R2011a で導入

参考

genss

説明

作成

プロパティ

Blocks — 制御設計ブロック 構造体

A,B,C,D — 調整可能なパラメーターおよび不確かさをもつパラメーターに対する状態空間行列の依存関係 genmat オブジェクト | umat オブジェクト | double の配列

E — E 行列 double の行列

StateName — 状態名 各状態に対して '' (既定値) | 文字ベクトル | 文字ベクトルの cell 配列

StateUnit — 状態単位のラベル 文字ベクトル | 文字ベクトルの cell 配列 | ''

InternalDelay — 内部遅延 スカラー | ベクトル

InputDelay — 入力遅延 すべての出力チャネルに対して 0 | スカラー | ベクトル

OutputDelay — 出力遅延 すべての出力チャネルに対して 0 | スカラー | ベクトル

Ts — サンプル時間 0 (連続時間) (既定値) | -1 (離散時間) | スカラー

TimeUnit — 時間変数の単位 'seconds' (既定値)

InputName — 入力チャネル名 文字ベクトル | 文字ベクトルの cell 配列

InputUnit — 入力チャネル単位 文字ベクトル | 文字ベクトルの cell 配列

InputGroup — 入力チャネル グループ 構造体

OutputName — 出力チャネル名 文字ベクトル | 文字ベクトルの cell 配列

OutputUnit — 出力チャネル単位 文字ベクトル | 文字ベクトルの cell 配列

OutputGroup — 出力チャネル グループ struct (既定値)

Name — システム名 文字ベクトル

Notes — システムに関連付ける任意のテキスト string | 文字ベクトルの cell 配列

UserData — システムに関連付ける任意のデータ型 任意の MATLAB® データ

SamplingGrid — モデル配列のサンプリング グリッド [] (既定値) | 構造体

オブジェクト関数

応答の抽出

ブロックおよび値へのアクセス

線形解析

モデルの相互接続

コントローラーの調整

例

調整可能なローパス フィルター

固定パラメーターと調整可能なパラメーターの両方をもつ状態空間モデルの作成

数値および調整可能なコンポーネントの両方をもつ制御システム モデル

一般化状態空間モデルの状態名の追跡

状態空間行列のパラメーターへの依存関係

ヒント

バージョン履歴

参考

トピック

`Blocks` — 制御設計ブロック
構造体

`A,B,C,D` — 調整可能なパラメーターおよび不確かさをもつパラメーターに対する状態空間行列の依存関係
`genmat` オブジェクト | `umat` オブジェクト | double の配列

`E` — E 行列
double の行列

`StateName` — 状態名
各状態に対して `''` (既定値) | 文字ベクトル | 文字ベクトルの cell 配列

`StateUnit` — 状態単位のラベル
文字ベクトル | 文字ベクトルの cell 配列 | `''`

`InternalDelay` — 内部遅延
スカラー | ベクトル

`InputDelay` — 入力遅延
すべての出力チャネルに対して `0` | スカラー | ベクトル

`OutputDelay` — 出力遅延
すべての出力チャネルに対して `0` | スカラー | ベクトル

`Ts` — サンプル時間
`0` (連続時間) (既定値) | `-1` (離散時間) | スカラー

`TimeUnit` — 時間変数の単位
`'seconds'` (既定値)

`InputName` — 入力チャネル名
文字ベクトル | 文字ベクトルの cell 配列

`InputUnit` — 入力チャネル単位
文字ベクトル | 文字ベクトルの cell 配列

`InputGroup` — 入力チャネルグループ
構造体

`OutputName` — 出力チャネル名
文字ベクトル | 文字ベクトルの cell 配列

`OutputUnit` — 出力チャネル単位
文字ベクトル | 文字ベクトルの cell 配列

`OutputGroup` — 出力チャネルグループ
`struct` (既定値)

`Name` — システム名
文字ベクトル

`Notes` — システムに関連付ける任意のテキスト
string | 文字ベクトルの cell 配列

`UserData` — システムに関連付ける任意のデータ型
任意の MATLAB^® データ

`SamplingGrid` — モデル配列のサンプリンググリッド
`[]` (既定値) | 構造体

調整可能なローパスフィルター

数値および調整可能なコンポーネントの両方をもつ制御システムモデル