margin
ゲイン余裕、位相余裕、および交差周波数
構文
説明
余裕のプロット
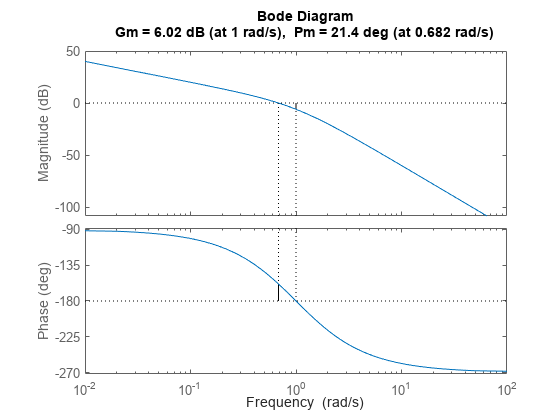
margin( は、画面に sys)sys のボード線図をプロットし、そのプロットのゲイン余裕と位相余裕を示します。ゲイン余裕はプロットに dB で表されます。
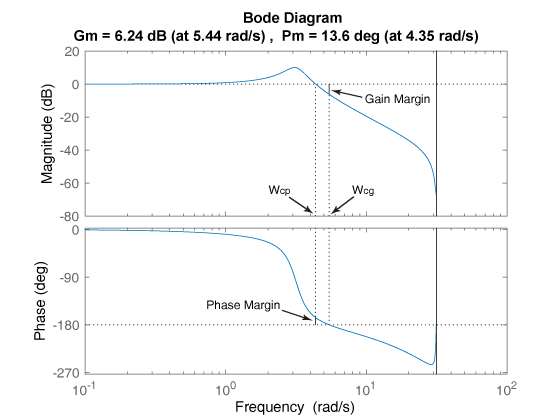
垂直の実線でゲイン余裕と位相余裕をマークします。垂直の破線は、位相余裕の測定される周波数 Wcp の位置と、ゲイン余裕の測定される周波数 Wcg の位置を示します。プロットのタイトルには、ゲイン余裕と位相余裕の振幅と位置が含まれます。
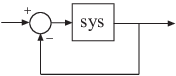
システムの Gm と Pm は、次の図に示すように、1 つの負のフィードバックを sys に適用することによって形成された閉ループ システムの相対的安定性を示します。
Gm は、位相角が –180° (360°を法とする) の周波数 Wcg でループ ゲインを 1 にするために必要なゲイン分散量です。言い換えれば、ゲイン余裕は g が位相特性 –180°における周波数のゲインの場合、1/g です。同様に、位相余裕はループ ゲインが 1.0 のときの応答の位相と –180°との間の差です。振幅が 1.0 の周波数 Wcp は、"ユニティーゲイン周波数" または "ゲイン交差周波数" と呼ばれます。sys に複数の交差がある場合、margin は、ゲイン余裕が 0 dB に最も近く、位相余裕が 0°に最も近い周波数を示します。
通常、3 以上のゲイン余裕と 30°～ 60°の位相余裕の組み合わせでは、帯域幅と安定性の間のトレードオフが適切になります。ただし、一部の多変数システムでは、異なる周波数において、はるかに小さいゲインと位相の変動で安定性が失われることがあります。そのようなシステムについては、"ディスク余裕" の概念によって、より信頼性の高い実際のゲイン余裕と位相余裕の推定が得られます。ディスク余裕の詳細については、diskmargin (Robust Control Toolbox) を参照してください。
余裕の値
[ は、Gm,Pm,Wcg,Wcp] = margin(sys)sys のゲイン余裕 Gm (絶対単位)、位相余裕 Pm およびそれに対応する周波数 Wcg と Wcp を返します。Wcg はゲイン余裕が測定される周波数で、–180°の位相交差周波数です。Wcp は位相余裕が測定される周波数で、0 dB のゲイン交差周波数です。これらの周波数はラジアン/TimeUnit で表され、TimeUnit は sys の TimeUnit プロパティで指定された単位になります。sys に複数の交差がある場合、margin は最小のゲイン余裕と位相余裕および対応する周波数を返します。
margin は、システムが内的に安定していない場合に警告を返します。つまり、システムが安定した閉ループでない場合、または開いている左半平面の外側に極-零点相殺がある場合です。
例
この例では、連続伝達関数を作成します。
sys = tf(1,[1 2 1 0])
sys =
1
---------------
s^3 + 2 s^2 + s
Continuous-time transfer function.
Model Properties
ゲイン余裕と位相余裕をグラフィック表示します。
margin(sys)
タイトルに表示されるゲイン余裕 (6.02 dB) と位相余裕 (21.4 度) は垂直の実線でマークされています。垂直の破線は、ゲイン余裕の測定される周波数 Wcg の位置と、位相余裕の測定される周波数 Wcp の位置を示します。
この例では、離散時間の伝達関数を作成します。
sys = tf([0.04798 0.0464],[1 -1.81 0.9048],0.1)
sys = 0.04798 z + 0.0464 --------------------- z^2 - 1.81 z + 0.9048 Sample time: 0.1 seconds Discrete-time transfer function. Model Properties
ゲイン余裕、位相余裕、および周波数を計算します。
[Gm,Pm,Wcg,Wcp] = margin(sys)
Gm = 2.0519
Pm = 13.5711
Wcg = 5.4376
Wcp = 4.3544
この結果は、位相交差周波数 5.43 rad/s でゲインの変動が 2.05 (6.24 dB) を超えると、システムが不安定になることを示しています。同様に、ゲイン交差周波数 4.35 rad/s で位相の変動が 13.57 度を超えると、システムは安定性を失います。
R2024a 以降
用途によっては、特定の周波数範囲における安定余裕を計算し、この範囲外のダイナミクスは無視する場合があります。たとえば、相対的に低い周波数と相対的に高い周波数の両方にダイナミクスがある次のシステムについて考えます。
sys = tf(5,[1 1 10]) + tf(5e3,[1 20 1e4]); damp(sys)
Pole Damping Frequency Time Constant
(rad/seconds) (seconds)
-5.00e-01 + 3.12e+00i 1.58e-01 3.16e+00 2.00e+00
-5.00e-01 - 3.12e+00i 1.58e-01 3.16e+00 2.00e+00
-1.00e+01 + 9.95e+01i 1.00e-01 1.00e+02 1.00e-01
-1.00e+01 - 9.95e+01i 1.00e-01 1.00e+02 1.00e-01
閉ループ システム CL = feedback(sys,1) の低い周波数での摂動に対する安定性は、高い周波数におけるものとは異なる場合があります。この違いを確認するには Focus オプションを使用します。まず、10 rad/s 未満の余裕を調べます。
[GmL,PmL,WcgL,WcpL] = margin(sys,Focus=[0 10])
GmL = Inf
PmL = 80.9920
WcgL = NaN
WcpL = 3.5137
約 10 rad/s の余裕を調べます。
[GmH,PmH,WcgH,WcpH] = margin(sys,Focus=[10 Inf])
GmH = Inf
PmH = 28.6437
WcgH = Inf
WcpH = 119.9618
この例では、w の周波数で測定された振幅 (m) および位相値 (p) で構成される、開ループ システムの周波数応答データを読み込みます。
load('openLoopFRD.mat','p','m','w');
ゲイン余裕と位相余裕を計算します。
[Gm,Pm,Wcg,Wcp] = margin(m,p,w)
Gm = 0.6249
Pm = 48.9853
Wcg = 1.2732
Wcp = 1.5197
この例では、倒立振子モデルを含む 3 行 3 列の配列が格納された invertedPendulumArray.mat を読み込みます。振子の質量は sys の単一の列に沿ってモデル間を移動するにつれて変化し、振子の長さは単一の行に沿って移動するにつれて変化します。質量の値には 100g、200g、300g、振子の長さには 3m、2m、1m がそれぞれ使用されます。
load('invertedPendulumArray.mat','sys'); size(sys)
3x3 array of transfer functions. Each model has 1 outputs and 1 inputs.
配列内のすべてのモデルのゲイン余裕と位相余裕を見つけます。
[Gm,Pm] = margin(sys)
Gm = 3×3
0.9800 0.9800 0.9800
0.9800 0.9800 0.9800
0.9800 0.9800 0.9800
Pm = 3×3
-11.3798 -11.4118 -11.4433
-11.4059 -11.4296 -11.4532
-11.4228 -11.4410 -11.4592
margin は、Gm と Pm の 2 つの配列を返し、その各エントリは sys の対応するエントリのゲイン余裕と位相余裕の値です。たとえば、重さ 100g、長さ 2m の振子のモデルの場合、ゲイン余裕と位相余裕はそれぞれ Gm(1,2) と Pm(1,2) になります。
入力引数
出力引数
ヒント
margin(mag,phase,w)を使用する場合、marginは内挿に依存して余裕を近似します。このため、一般に結果の精度は低下します。たとえば、0 dB 交差がw範囲内にない場合、marginは位相余裕Infを返します。したがって、解析モデルsysがある場合、[Gm,Pm,Wcg,Wcp] = margin(sys)を使用すると、よりロバストな方法で余裕を取得できます。Robust Control Toolbox™ ソフトウェアがある場合、フィードバック ループの安定性が維持される "安全" なゲインと位相の変動の範囲を定義するディスクベースの余裕を
diskmargin(Robust Control Toolbox) を使用して計算できます。
