mechss

スパース 2 次状態空間モデル

R2020b 以降

説明

有限要素解析 (FEA) パッケージから取得された行列を使用して 2 次スパース モデルを表すには mechss を使用します。このようなスパース モデルは有限要素解析 (FEA) から発生し、構造解析、流体の流れ、熱伝達、電磁などの分野で役立ちます。このタイプのモデル化による結果の行列は、1 つのスパース パターンで非常に大規模になります。したがって、線形解析を実行するときに MATLAB^® でこのような大きな状態空間モデルを表すには、mechss を使用するのが効率的です。また、mechss を使用して 1 次 sparss モデル オブジェクトまたは他の動的システム モデルを mechss オブジェクトに変換することもできます。

mechss モデル オブジェクトを使用して、SISO または MIMO 状態空間モデルを連続時間または離散時間で表現できます。連続時間では、2 次スパース マス-バネ-ダンパー モデルは次の形式で表されます。

$$\begin{array}{r}\text{M }\ddot{q}(t)+\text{C }\dot{q}(t)+\text{K }q(t)\text{ = B }u(t)\\ y(t)\text{ = F }q(t)+\text{G }\dot{q}(t)+\text{D }u(t)\end{array}$$

ここで、完全な状態ベクトルは $$\left[q,\dot{q}\right]$$ で表され、この $$q$$ および $$\dot{q}$$ は変位ベクトルと速度ベクトルです。u および y はそれぞれ入力と出力を表します。M、C および K はそれぞれ質量、減衰および剛性を表します。B は入力行列で、F と G はそれぞれ変位と速度の出力行列です。D は入力から出力への行列です。

mechss オブジェクトを使用して、次を実行できます。

• 時間領域および周波数領域応答解析を実行します。

• 他の LTI モデルとの信号ベースの接続を指定します。

• interface コマンドを使用してコンポーネント間の物理インターフェイスを指定します。

詳細については、スパース モデルの基礎を参照してください。

作成

構文

sys = mechss(M,C,K,B,F,G,D)

sys = mechss(M,C,K,B,F,G,D,ts)

sys = mechss(M,C,K)

sys = mechss(D)

sys = mechss(___,Name,Value)

sys = mechss(ltiSys)

説明

sys = mechss(M,C,K,B,F,G,D) は、次の連続時間の 2 次マス-バネ-ダンパー モデルを表す mechss オブジェクトを作成します。

$$\begin{array}{r}\text{M }\ddot{q}(t)+\text{C }\dot{q}(t)+\text{K }q(t)\text{ = B }u(t)\\ y(t)\text{ = F }q(t)+\text{G }\dot{q}(t)+\text{D }u(t)\end{array}$$

ここで、M、C、および K はそれぞれ質量、減衰、および剛性行列を表します。B は入力から状態への行列で、F と G は、状態 x の 2 つのコンポーネントから得られた、変位から出力への行列と速度から出力への行列です。D は入力から出力への行列です。質量行列が単位行列の場合、M を [] に設定できます。G と D を [] に設定するか、空の場合は省略できます。

sys = mechss(M,C,K,B,F,G,D,ts) は、サンプル時間 ts を使用して、次の離散時間の 2 次マス-バネ-ダンパー モデルを表す mechss オブジェクトを作成します。

$$\begin{array}{r}\text{M }q\left[k+2\right]+\text{C }q\left[k+1\right]+\text{K }q\left[k\right]\text{ = B }u\left[k\right]\\ y\left[k\right]\text{ = F }q\left[k\right]+\text{G }q\left[k+1\right]+\text{D }u\left[k\right]\end{array}$$

サンプル時間を未指定のままにする場合は、ts を -1 に設定します。

sys = mechss(M,C,K) は、以下を前提として mechss モデル オブジェクトを作成します。

• 質量行列 M と同じサイズの B および F の単位行列

• G および D のゼロからなる行列

sys = mechss(D) は、静的ゲイン D を表す mechss モデル オブジェクトを作成します。出力スパース状態空間モデルは mechss([],[],[],[],[],[],D) と等価です。

sys = mechss(___,Name,Value) は、1 つ以上の名前と値のペアの引数を使用して 2 次スパース状態空間モデルのプロパティを設定します。この構文は、前述の任意の入力引数の組み合わせで使用します。

sys = mechss(ltiSys) は、動的システム モデル ltiSys を 2 次スパース状態空間モデルに変換します。

入力引数

M — 質量行列

Nq 行 Nq 列のスパース行列

質量行列。Nq 行 Nq 列のスパース行列として指定します。ここで Nq は自由度の数です。この入力はプロパティ M の値を設定します。

C — 減衰行列

Nq 行 Nq 列のスパース行列

減衰行列。Nq 行 Nq 列のスパース行列として指定します。ここで、Nq は自由度の数です。C=[] を設定して零点の減衰を指定することもできます。この入力はプロパティ C の値を設定します。

K — 剛性行列

Nq 行 Nq 列のスパース行列

剛性行列。Nq 行 Nq 列のスパース行列として指定します。ここで Nq は自由度の数です。この入力はプロパティ K の値を設定します。

B — 入力から状態への行列

Nq 行 Nu 列のスパース行列

入力から状態への行列。Nq 行 Nu 列のスパース行列として指定します。ここで Nq は自由度の数、Nu は入力の数です。この入力はプロパティ B の値を設定します。

F — 変位から出力への行列

Ny 行 Nq 列のスパース行列

変位から出力への行列。Ny 行 Nq 列のスパース行列として指定します。ここで Nq は自由度の数、Ny は出力の数です。この入力はプロパティ F の値を設定します。

G — 速度から出力への行列

Ny 行 Nq 列のスパース行列

速度から出力への行列。Ny 行 Nq 列のスパース行列として指定します。ここで Nq は自由度の数、Ny は出力の数です。この入力はプロパティ G の値を設定します。

D — 入力から出力への行列

Ny 行 Nu 列のスパース行列

入力から出力への行列。Ny 行 Nu 列のスパース行列として指定します。ここで Ny は出力の数、Nu は入力の数です。この入力はプロパティ D の値を設定します。

ts — サンプル時間

スカラー

スカラーとして指定されたサンプル時間。詳細については、Ts プロパティを参照してください。

ltiSys — 2 次スパース状態空間形式に変換する動的システム

動的システム モデル | モデル配列

2 次スパース状態空間形式に変換する動的システム。SISO または MIMO 動的システム モデル、または動的システム モデルの配列として指定します。変換できる動的システムには次のものが含まれます。

• sparss、tf、zpk、ss、pid モデルなどの連続時間または離散時間の数値 LTI モデル。

出力引数

sys — 出力システム モデル

mechss モデル オブジェクト

出力システム モデル。mechss モデル オブジェクトとして返されます。

プロパティ

M — 質量行列

Nq 行 Nq 列のスパース行列

質量行列。Nq 行 Nq 列のスパース行列として指定します。ここで Nq は自由度の数です。

C — 減衰行列

Nq 行 Nq 列のスパース行列

減衰行列。Nq 行 Nq 列のスパース行列として指定します。ここで、Nq は自由度の数です。

K — 剛性行列

Nq 行 Nq 列のスパース行列

減衰行列。Nq 行 Nq 列のスパース行列として指定します。ここで、Nq は自由度の数です。

B — 入力から状態への行列

Nq 行 Nu 列のスパース行列

入力から状態への行列。Nq 行 Nu 列のスパース行列として指定します。ここで Nq は自由度の数、Nu は入力の数です。

F — 変位から出力への行列

Ny 行 Nq 列のスパース行列

変位から出力への行列。Ny 行 Nq 列のスパース行列として指定します。ここで Nq は自由度の数、Ny は出力の数です。

G — 速度から出力への行列

Ny 行 Nq 列のスパース行列

速度から出力への行列。Ny 行 Nq 列のスパース行列として指定します。ここで Nq は自由度の数、Ny は出力の数です。

D — 入力から出力への行列

Ny 行 Nu 列のスパース行列

入力から出力への行列。Ny 行 Nu 列のスパース行列として指定します。ここで Ny は出力の数、Nu は入力の数です。D は静的ゲイン行列とも呼ばれ、定常状態の条件下での入力に対する出力の比率を表します。

StateInfo — 状態区分情報

構造体配列

状態ベクトル コンポーネント、コンポーネント間のインターフェイス、およびコンポーネントを接続する内部信号を含む状態区分情報。次のフィールドを含む構造体配列として指定します。

• Type — タイプにはコンポーネント、信号、または物理インターフェイスが含まれる

• Name — コンポーネント、信号、または物理インターフェイスの名前

• Size — 区分内の状態の数または自由度

showStateInfo を使用してスパース状態空間モデルの区分情報を表示できます。また、xsort を使用してスパース モデルで区分を並べ替えることもできます。

SolverOptions — モデル解析のオプション

構造体

モデル解析のオプション。次のフィールドをもつ構造体として指定します。

• UseParallel —並列計算を有効にする場合はこのオプションを true に設定し、無効にする場合は false に設定します。並列計算は既定で無効になっています。UseParallel オプションには、Parallel Computing Toolbox™ ライセンスが必要です。

• DAESolver — このオプションを使用して微分代数方程式 (DAE) ソルバーのタイプを選択します。次の DAE ソルバーが使用できます。

  • 'trbdf2' — 精度 o(h^2) の固定ステップ ソルバー。ここで、h はステップ サイズです。[2]これは mechss モデル オブジェクトの既定のソルバーです。

  • 'trbdf3' — 精度 o(h^3) の固定ステップ ソルバー。ここで、h はステップ サイズです。

  • 'hht' — 精度 o(h^2) の固定ステップ ソルバー。ここで、h はステップ サイズです。[1]

  ステップ サイズを小さくすると、精度が向上し、数値的減衰が無視される周波数範囲が広がります。'hht' は最速ですが、初期加速度が高い場合 (初期加速度でのインパルス応答など) 困難になる場合があります。'trbdf2' では 'hht' のおよそ 2 倍の計算が必要で、'trbdf3' では 'trbdf2' よりもさらに 50% 多くの計算が必要です。

  例については、スパース 2 次モデルの時間および周波数応答を参照してください。

InternalDelay — モデルの内部遅延

ベクトル

モデルの内部遅延。ベクトルとして指定します。内部遅延は、たとえば、システムで遅延のあるフィードバック ループを閉じるときや、遅延システムを順番にまたは並列で接続するときに生じます。内部遅延の詳細については、むだ時間のある閉フィードバック ループを参照してください。

連続時間モデルの場合、内部遅延はモデルの TimeUnit プロパティで指定された時間単位で表現されます。離散時間モデルの場合、内部遅延はサンプル時間 Ts の整数倍として表現されます。たとえば、InternalDelay = 3 は 3 サンプリング周期の遅延を意味します。

内部遅延の値はプロパティ InternalDelay を使用して変更できます。ただし、sys.InternalDelay のエントリの数は、モデルの構造に組み込まれているので変更できません。

InputDelay — 入力遅延

0 (既定値) | スカラー | Nu 行 1 列のベクトル

各入力チャネルの入力遅延。次のいずれかとして指定します。

• スカラー — SISO システムに入力遅延を、または多入力システムのすべての入力に同じ遅延を指定します。

• Nu 行 1 列のベクトル — 多入力システムの入力に別々の入力遅延を指定します。Nu は入力の数です。

連続時間システムの場合は、TimeUnit プロパティによって指定された時間単位で入力遅延を指定します。離散時間システムの場合は、サンプル時間 Ts の整数倍で入力遅延を指定します。

詳細については、線形システムでのむだ時間を参照してください。

OutputDelay — 出力遅延

0 (既定値) | スカラー | Ny 行 1 列のベクトル

各出力チャネルの出力遅延。次のいずれかとして指定します。

• スカラー — SISO システムに出力遅延を、または多出力システムのすべての出力に同じ遅延を指定します。

• Ny 行 1 列のベクトル — 多出力システムの出力に別々の出力遅延を指定します。Ny は出力の数です。

連続時間システムの場合は、TimeUnit プロパティによって指定された時間単位で出力遅延を指定します。離散時間システムの場合は、サンプル時間 Ts の整数倍で出力遅延を指定します。

詳細については、線形システムでのむだ時間を参照してください。

Ts — サンプル時間

0 (既定値) | 正のスカラー | -1

サンプル時間。以下として指定します。

• 0 (連続時間システムの場合)。

• 離散時間システムのサンプリング周期を表す正のスカラー。Ts は TimeUnit プロパティによって指定される時間単位で指定します。

• -1 (サンプル時間が指定されていない離散時間システムの場合)。

メモ

Ts を変更してもモデルの離散化やリサンプリングは行われません。連続時間表現と離散時間表現の間の変換を行うには、c2d と d2c を使用します。離散時間システムのサンプル時間を変更するには、d2d を使用します。

TimeUnit — 時間変数の単位

'seconds' (既定値) | 'nanoseconds' | 'microseconds' | 'milliseconds' | 'minutes' | 'hours' | 'days' | 'weeks' | 'months' | 'years' | ...

時間変数の単位。次のいずれかとして指定します。

• 'nanoseconds'

• 'microseconds'

• 'milliseconds'

• 'seconds'

• 'minutes'

• 'hours'

• 'days'

• 'weeks'

• 'months'

• 'years'

TimeUnit の変更は他のプロパティには影響しませんが、システム全体の動作が変わります。chgTimeUnit を使用して、システム動作を変更せずに時間単位を変換します。

InputName — 入力チャネル名

'' (既定値) | 文字ベクトル | 文字ベクトルの cell 配列

入力チャネル名。以下のいずれかとして指定します。

• 文字ベクトル (単入力モデルの場合)。

• 文字ベクトルの cell 配列 (多入力モデルの場合)。

• '' (いずれの入力チャネルにも名前を指定しない場合)。

あるいは、自動的なベクトル拡張を使用して多入力モデルの入力名を割り当てることもできます。たとえば、sys が 2 入力モデルである場合は、以下のように入力します。

sys.InputName = 'controls';

入力名は自動的に {'controls(1)';'controls(2)'} へと拡張されます。

省略形表記 u を使用して、InputName プロパティを参照できます。たとえば、sys.u は sys.InputName と同じです。

InputName の使用目的は次のとおりです。

• モデル表示とプロット上のチャネルの識別

• MIMO システムのサブシステムの抽出

• モデル相互接続時における接続点の指定

InputUnit — 入力チャネル単位

'' (既定値) | 文字ベクトル | 文字ベクトルの cell 配列

入力チャネル単位。以下のいずれかとして指定します。

• 文字ベクトル (単入力モデルの場合)。

• 文字ベクトルの cell 配列 (多入力モデルの場合)。

• '' (いずれの入力チャネルにも単位を指定しない場合)。

InputUnit を使用して入力信号の単位を指定します。InputUnit はシステムの動作に影響しません。

InputGroup — 入力チャネル グループ

構造体

入力チャネル グループ。構造体として指定します。InputGroup プロパティを使用して、MIMO システムの入力チャネルをグループに割り当て、各グループを名前で参照します。InputGroup のフィールド名はグループ名であり、フィールドの値は各グループの入力チャネルです。たとえば、入力チャネル 1 と 2、および 3 と 5 をそれぞれ含む、controls および noise という名前の入力グループを作成するには、次のように入力します。

sys.InputGroup.controls = [1 2];
sys.InputGroup.noise = [3 5];

その後、以下を使用して controls 入力からすべての出力にサブシステムを抽出できます。

sys(:,'controls')

既定では、InputGroup はフィールドのない構造体です。

OutputName — 出力チャネル名

'' (既定値) | 文字ベクトル | 文字ベクトルの cell 配列

出力チャネル名。次のいずれかとして指定されます。

• 文字ベクトル (単出力モデルの場合)。

• 文字ベクトルの cell 配列 (多出力モデルの場合)。

• '' (いずれの出力チャネルにも名前を指定しない場合)。

あるいは、自動的なベクトル拡張を使用して多出力モデルの出力名を割り当てることもできます。たとえば、sys が 2 出力モデルである場合は、以下のように入力します。

sys.OutputName = 'measurements';

出力名は自動的に {'measurements(1)';'measurements(2)'} へと拡張されます。

省略形表記 y を使用して OutputName プロパティを参照することもできます。たとえば、sys.y は sys.OutputName と同じです。

OutputName の使用目的は次のとおりです。

• モデル表示とプロット上のチャネルの識別

• MIMO システムのサブシステムの抽出

• モデル相互接続時における接続点の指定

OutputUnit — 出力チャネル単位

'' (既定値) | 文字ベクトル | 文字ベクトルの cell 配列

出力チャネル単位。次のいずれかとして指定されます。

• 文字ベクトル (単出力モデルの場合)。

• 文字ベクトルの cell 配列 (多出力モデルの場合)。

• '' (いずれの出力チャネルにも単位を指定しない場合)。

OutputUnit を使用して出力信号の単位を指定します。OutputUnit はシステムの動作に影響しません。

OutputGroup — 出力チャネル グループ

構造体

出力チャネル グループ。構造体として指定します。OutputGroup を使用して、MIMO システムの出力チャネルをグループに割り当て、各グループを名前で参照します。OutputGroup のフィールド名はグループ名であり、フィールドの値は各グループの出力チャネルです。たとえば、出力チャネル 1、および 3 と 5 をそれぞれ含む、temperature および measurement という名前の出力グループを作成します。

sys.OutputGroup.temperature = [1];
sys.OutputGroup.measurement = [3 5];

その後、以下を使用してすべての入力から measurement 出力にサブシステムを抽出できます。

sys('measurement',:)

既定では、OutputGroup はフィールドのない構造体です。

Notes — ユーザー指定のテキスト

{} (既定値) | 文字ベクトル | 文字ベクトルの cell 配列

システムに関連付けるユーザー指定のテキスト。文字ベクトルまたは文字ベクトルの cell 配列として指定します。たとえば、'System is MIMO' とします。

UserData — ユーザー指定のデータ

[] (既定値) | 任意の MATLAB データ型

システムに関連付けるユーザー指定のデータ。任意の MATLAB データ型として指定します。

Name — システム名

'' (既定値) | 文字ベクトル

システム名。文字ベクトルとして指定します。たとえば、'system_1' とします。

SamplingGrid — モデル配列のサンプリング グリッド

構造体配列

モデル配列のサンプリング グリッド。構造体配列として指定します。

SamplingGrid を使用して、モデル配列の各モデルに関連付けられている変数値を追跡します。

構造体のフィールド名をサンプリング変数の名前に設定します。フィールドの値を、配列内の各モデルに関連付けられているサンプリングされた変数の値に設定します。すべてのサンプリング変数は数値スカラーでなければならず、サンプル値のすべての配列はモデル配列の次元と一致しなければなりません。

たとえば、t = 0:10 の各時点で線形時変システムのスナップショットを記録することにより、線形モデルの 11 行 1 列の配列 sysarr を作成することができます。次のコードは線形モデルでの時間サンプルを格納します。

 sysarr.SamplingGrid = struct('time',0:10)

同様に、2 つの変数 zeta と w を個別にサンプリングすることにより、6 行 9 列のモデル配列 M を作成できます。次のコードは (zeta,w) の値を M にマッピングします。

[zeta,w] = ndgrid(<6 values of zeta>,<9 values of w>)
M.SamplingGrid = struct('zeta',zeta,'w',w)

既定では、SamplingGrid はフィールドのない構造体です。

オブジェクト関数

以下のリストに、mechss モデル オブジェクトで使用できる関数を示します。

モデル化

sparss	スパース 1 次状態空間モデル
getx0	初期条件を mechss オブジェクトから sparss オブジェクトにマッピング
full	スパース モデルを密度の高いストレージに変換する
imp2exp	陰的な線形関係を陽的な入力と出力の関係に変換
inv	動的システム モデルを反転
getDelayModel	内部遅延の状態空間表現

データ アクセス

sparssdata	1 次スパース状態空間モデル データにアクセスする
mechssdata	2 次スパース状態空間モデル データにアクセスする
showStateInfo	スパース モデルの状態ベクトルのマッピング
spy	スパース モデルのスパース パターンを可視化する

時間および周波数応答

step	動的システムのステップ応答
impulse	動的システムのインパルス応答プロット、インパルス応答データ
initial	状態空間モデルの初期状態に対するシステム応答
lsim	任意の入力に対する動的システムの時間応答シミュレーション データを計算
bode	動的システムのボード周波数応答
nyquist	動的システムのナイキスト応答
nichols	動的システムのニコルス応答
sigma	動的システムの周波数応答の特異値
passiveplot	受動性インデックスの周波数の関数としての計算またはプロット
dcgain	LTI システムの低周波数 (DC) ゲイン
evalfr	指定した周波数でのシステム応答の評価
freqresp	周波数のグリッドでのシステム応答の評価

モデルの相互接続

interface	mechss モデルのコンポーネント間の物理接続の指定
xsort	状態区分に基づいて状態を並べ替える
feedback	複数のモデルのフィードバック接続
parallel	2 つのモデルの並列接続
append	入力と出力を追加して、モデルをグループ化する
connect	動的システムのブロック線図相互接続
lft	2 つのモデルの一般化されたフィードバック相互接続 (Redheffer スター積)
series	2 つのモデルの直列接続

例

連続時間スパース 2 次モデル

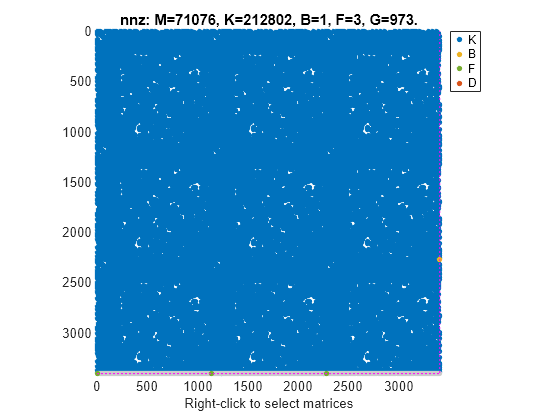
この例では、ファイル sparseBeam.mat で先端に衝撃点荷重が適用される 3 次元ビーム モデルのスパース行列を考えてみます。

sparseBeam.mat からスパース行列を抽出します。

load('sparseBeam.mat','M','K','B','F','G','D');

減衰がないため、行列 C に [] を指定して mechss モデル オブジェクトを作成します。

sys = mechss(M,[],K,B,F,G,D)

Sparse continuous-time second-order model with 3 outputs, 1 inputs, and 3408 degrees of freedom.

Use "spy" and "showStateInfo" to inspect model structure. 
Type "help mechssOptions" for available solver options for this model.

出力 sys は、3408 の自由度、1 つの入力、および 3 つの出力をもつスパース モデルの 3 行 1 列の配列を含む mechss モデル オブジェクトです。

spy コマンドを使用して、mechss モデル オブジェクトのスパース性を可視化できます。

spy(sys)

離散時間スパース 2 次モデル

この例では、ファイル discreteSOSparse.mat の離散システムのスパース行列について考えてみます。

discreteSOSparse.mat からスパース行列を読み込みます。

load('discreteSOSparse.mat','M','C','K','B','F','G','D','ts');

サンプル時間 ts を指定して離散時間 mechss モデル オブジェクトを作成します。

sys = mechss(M,C,K,B,F,G,D,ts)

Sparse discrete-time second-order model with 1 outputs, 1 inputs, and 28408 degrees of freedom.

Use "spy" and "showStateInfo" to inspect model structure. 
Type "help mechssOptions" for available solver options for this model.

出力 sys は、28408 の自由度、1 つの入力および 1 つの出力をもつ離散時間 mechss モデル オブジェクトです。

spy コマンドを使用して、mechss モデル オブジェクトのスパース パターンを可視化できます。プロットを右クリックして、表示する行列を選択します。

spy(sys)

スパース 2 次モデルの配列

この例では、複数のスパース 2 次状態空間モデルを定義する 3 つのスパース行列セットを含む sparseSOArray.mat について考えます。

sparseSOArray.mat からデータを抽出します。

load('sparseSOArray.mat');

mechss モデルの 3 行 1 列の配列を事前に割り当てます。

sys = mechss(zeros(1,1,3));

次に、インデックス付きの代入を使用して、3 行 1 列の配列にスパース 2 次モデルを設定します。

sys(:,:,1) = mechss(M1,[],K1,B1,F1,G1,[]);
sys(:,:,2) = mechss(M2,[],K2,B2,F2,G2,[]);
sys(:,:,3) = mechss(M3,[],K3,B3,F3,G3,[]);
size(sys)

3x1 array of sparse second-order models.
Each model has 1 outputs, 1 inputs, and between 385 and 738 degrees of freedom.

または、I/O サイズが同じモデルがある場合は、stackコマンドを使用してスパース 2 次モデルの配列を作成することもできます。

Copyright 2020 The MathWorks, Inc.

静的ゲインの MIMO スパース 2 次モデル

静的ゲインの MIMO スパース 2 次状態空間モデルを作成します。

次の 2 入力、3 出力の静的ゲイン行列について考えます。

$$D=\left[\begin{array}{cc}1& 5\\ 2& 3\\ 5& 9\end{array}\right]$$

ゲイン行列を指定して静的ゲインのスパース 2 次状態空間モデルを作成します。

D = [1,5;2,3;5,9];
sys = mechss(D);
size(sys)

Sparse second-order model with 3 outputs, 2 inputs, and 0 degrees of freedom.

マス-バネ-ダンパー スパース 2 次モデル

この例では、質量、剛性、および減衰スパース行列を含む sparseSOSignal.mat について考えます。

sparseSOSignal.mat からスパース行列を読み込み、スパース 2 次モデル オブジェクトを作成します。

load('sparseSOModel.mat','M','C','K');
sys = mechss(M,C,K);

mechss は、以下を前提として sys モデル オブジェクトを作成します。

• 質量行列 M と同じサイズの B および F の単位行列。

• G および D のゼロ行列。

1 次スパース モデルを 2 次スパース モデル表現に変換

この例では、sparss モデル オブジェクト ltiSys を含む sparssModel.mat について考えます。

sparssModel.mat から sparss モデル オブジェクトを読み込みます。

load('sparssModel.mat','ltiSys');
ltiSys

Sparse continuous-time state-space model with 1 outputs, 1 inputs, and 354 states.

Use "spy" and "showStateInfo" to inspect model structure. 
Type "help sparssOptions" for available solver options for this model.

mechss コマンドを使用して mechss モデル オブジェクト表現に変換します。

sys = mechss(ltiSys)

Sparse continuous-time second-order model with 1 outputs, 1 inputs, and 354 degrees of freedom.

Use "spy" and "showStateInfo" to inspect model structure. 
Type "help mechssOptions" for available solver options for this model.

スパース 2 次モデルの時間および周波数応答

この例では、tuningForkData.mat について考えます。このファイルには、腕の 1 本が素早く静かに打音される音叉のスパース 2 次モデルが含まれます。このシステムには 1 つの入力として、その腕の 1 本に加えられる圧力があり、これにより先端の変位と音叉の底部の 2 つの出力が生成されます。

tuningForkData.mat からワークスペースにスパース行列を読み込み、mechss モデル オブジェクトを作成します。

load('tuningForkData.mat','M','K','B','F');
sys = mechss(M,[],K,B,F,'InputName','pressure','Outputname',{'y tip','x base'})

次に、UseParallel パラメーターを true に設定し、trbdf3 を使用するように DAESolver を設定して、モデルのソルバー オプションを設定します。spy を使用して、モデル構造体を検査します。並列計算を有効にするには、Parallel Computing Toolbox™ のライセンスが必要です。

sys.SolverOptions.UseParallel = true;
sys.SolverOptions.DAESolver = 'trbdf3';
spy(sys)

showStateInfo を使用してコンポーネントを調べることもできます。

showStateInfo(sys)

step を使用して、システムのステップ応答プロットを取得します。スパース モデルの時間ベクトルまたは最終時間を指定する必要があります。

t = linspace(0,0.5,1000);
step(sys,t)

次に、ボード線図を取得して周波数応答を調べます。スパース モデルの周波数ベクトルを指定する必要があります。

w = logspace(1,5,1000);
bode(sys,w), grid

フィードバック ループのスパース 2 次モデル

この例では、スパース 2 次モデルを含む sparseSOSignal.mat について考えます。アクチュエータ、センサー、コントローラーを定義して、それらをフィードバック ループでプラントに接続します。

スパース行列を読み込み、mechss オブジェクトを作成します。

load sparseSOSignal.mat
plant = mechss(M,C,K,B,F,[],[],'Name','Plant');

次に、伝達関数を使用してアクチュエータとセンサーを作成します。

act = tf(1,[1 0.5 3],'Name','Actuator');
sen = tf(1,[0.02 7],'Name','Sensor');

プラントの PID コントローラー オブジェクトを作成します。

con = pid(1,1,0.1,0.01,'Name','Controller');

feedback コマンドを使用して、プラント、センサー、アクチュエータ、およびコントローラーをフィードバック ループ内で接続します。

sys = feedback(sen*plant*act*con,1)

Sparse continuous-time second-order model with 1 outputs, 1 inputs, and 7111 degrees of freedom.

Use "spy" and "showStateInfo" to inspect model structure. 
Type "help mechssOptions" for available solver options for this model.

mechss オブジェクトがどのモデル オブジェクト タイプよりも優先されるため、結果のシステム sys は mechss オブジェクトになります。

showStateInfo を使用してコンポーネントと信号グループを表示します。

showStateInfo(sys)

The state groups are:

    Type          Name       Size
  -------------------------------
  Component      Sensor         1
  Component      Plant       7102
  Signal                        1
  Component     Actuator        2
  Signal                        1
  Component    Controller       2
  Signal                        1
  Signal                        1

xsort を使用してコンポーネントと信号を並べ替えてから、コンポーネントと信号グループを表示します。

sysSort = xsort(sys);
showStateInfo(sysSort)

The state groups are:

    Type          Name       Size
  -------------------------------
  Component      Sensor         1
  Component      Plant       7102
  Component     Actuator        2
  Component    Controller       2
  Signal                        4

コンポーネントが信号区分の前に順序付けされていることを確認します。信号は並べ替えられて、単一の区分にグループ化されます。

spy を使用して結果のシステムのスパース パターンを可視化することもできます。

spy(sysSort)

スパース 2 次モデルのコンポーネント間の物理的接続

この例では、下の図に示すように、各頂点の支柱に連結されている 2 枚の四角形のプレートで構成される構造モデルを考えます。下のプレートは地面にしっかり取り付けられ、支柱は四角形のプレートの各頂点にしっかり取り付けられています。

platePillarModel.mat に含まれている有限要素モデル行列を読み込み、上記システムを表すスパース 2 次モデルを作成します。

load('platePillarModel.mat')
model = ...
   mechss(M1,[],K1,B1,F1,'Name','Plate1') + ...
   mechss(M2,[],K2,B2,F2,'Name','Plate2') + ...
   mechss(Mp,[],Kp,Bp,Fp,'Name','Pillar3') + ...
   mechss(Mp,[],Kp,Bp,Fp,'Name','Pillar4') + ...
   mechss(Mp,[],Kp,Bp,Fp,'Name','Pillar5') + ...
   mechss(Mp,[],Kp,Bp,Fp,'Name','Pillar6');
sys = model;

mechss モデル オブジェクトのコンポーネントを確認するには showStateInfo を使用します。

showStateInfo(sys)

The state groups are:

    Type        Name      Size
  ----------------------------
  Component    Plate1     2646
  Component    Plate2     2646
  Component    Pillar3     132
  Component    Pillar4     132
  Component    Pillar5     132
  Component    Pillar6     132

次に、相互作用する自由度 (DOF) インデックス データを dofData.mat から読み込み、interface を使用して 2 枚のプレートと 4 本の支柱間の物理的接続を作成します。dofs は、最初の 2 行に 1 枚目と 2 枚目のプレートの DOF インデックス データを含み、他の 4 行に 4 本の支柱のインデックス データを含む 6x7 の cell 配列です。関数は既定で、物理結合のデュアルアセンブリ メソッドを使用します。

load('dofData.mat','dofs')
for i=3:6
   sys = interface(sys,"Plate1",dofs{1,i},"Pillar"+i,dofs{i,1});
   sys = interface(sys,"Plate2",dofs{2,i},"Pillar"+i,dofs{i,2});
end

下のプレートと地面間の接続を指定します。

sysConDual = interface(sys,"Plate2",dofs{2,7});

物理インターフェイスを確認するには showStateInfo を使用します。

showStateInfo(sysConDual)

The state groups are:

    Type            Name         Size
  -----------------------------------
  Component        Plate1        2646
  Component        Plate2        2646
  Component       Pillar3         132
  Component       Pillar4         132
  Component       Pillar5         132
  Component       Pillar6         132
  Interface    Plate1-Pillar3      12
  Interface    Plate2-Pillar3      12
  Interface    Plate1-Pillar4      12
  Interface    Plate2-Pillar4      12
  Interface    Plate1-Pillar5      12
  Interface    Plate2-Pillar5      12
  Interface    Plate1-Pillar6      12
  Interface    Plate2-Pillar6      12
  Interface    Plate2-Ground        6

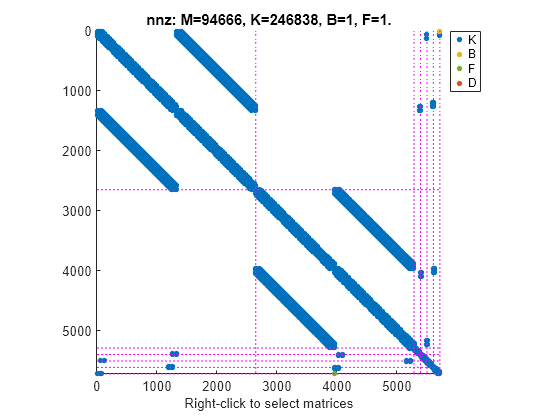
spy を使用して、最終モデルのスパース行列を可視化できます。

spy(sysConDual)

ここで、主要アセンブリ メソッドを使用して物理的接続を指定します。

sys = model;
for i=3:6
   sys = interface(sys,"Plate1",dofs{1,i},"Pillar"+i,dofs{i,1},'primal');
   sys = interface(sys,"Plate2",dofs{2,i},"Pillar"+i,dofs{i,2},'primal');
end
sysConPrimal = interface(sys,"Plate2",dofs{2,7},'primal');

物理インターフェイスを確認するには showStateInfo を使用します。

showStateInfo(sysConPrimal)

The state groups are:

    Type        Name      Size
  ----------------------------
  Component    Plate1     2646
  Component    Plate2     2640
  Component    Pillar3     108
  Component    Pillar4     108
  Component    Pillar5     108
  Component    Pillar6     108

主要アセンブリによって、グローバル有限要素メッシュ内の一連の共有 DOF に関連付けられた冗長な DOF の半分が取り除かれます。

spy を使用して、最終モデルのスパース行列を可視化できます。

spy(sysConPrimal)

この例のデータセットは、ASML の Victor Dolk によって提供されています。

参照

[1] H. Hilber, T. Hughes & R. Taylor. " Improved numerical dissipation for time integration algorithms in structural dynamics." Earthquake Engineering and Structural Dynamics, vol. 5, no. 3, pp. 283-292, 1977.

[2] M. Hosea and L. Shampine. "Analysis and implementation of TR-BDF2." Applied Numerical Mathematics, vol. 20, no. 1-2, pp. 21-37, 1996.

バージョン履歴

R2020b で導入

参考

sparss | mechssdata | showStateInfo | interface | xsort | full | spy | Sparse Second Order

トピック

• モデル コンポーネントの剛体アセンブリ
• 片持ちビームの線形解析
• スパース モデルの基礎