step
動的システムのステップ応答
構文
説明
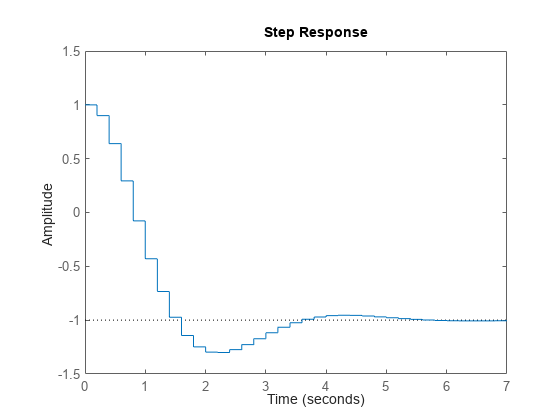
step は td 時間単位の後、U から U + dU までの入力値のステップ変化に対するステップ応答を計算します。

ここで
t0 はシミュレーション開始時間です。
td はステップ遅延です。
U はベースライン入力値 (バイアス) です。
dU はステップ振幅です。
既定では、関数は t0 = 0、U = 0、dU = 1、および td = 0 でステップを適用します。ただし、RespConfig を使用してこれらの値を構成できます。また、初期状態 x(t0) を指定することもできます。初期状態を指定しない場合、step では、初期状態としてシステムが入力レベル U で停止しているものと想定されます。
[ は、ステップ振幅や入力オフセットなど、ステップ応答を計算するための追加オプションを指定します。y,tOut] = step(___,config)RespConfig を使用して config を作成します。
step(___) は、前述のすべての入力引数の組み合わせについて、sys のステップ応答を既定のプロット オプションでプロットします。プロットをさらにカスタマイズするには、stepplot を使用します。
複数の動的システムの応答を同じプロット上にプロットするには、
sysをモデルのコンマ区切りリストとして指定します。たとえば、step(sys1,sys2,sys3)は 3 つのモデルの応答を同じプロット上にプロットします。プロット内の各システムの色、ライン スタイル、およびマーカーを指定するには、システムごとに
LineSpec値を指定します。たとえば、step(sys1,LineSpec1,sys2,LineSpec2)は 2 つのモデルをプロットし、それらのプロット スタイルを指定します。LineSpec値の指定の詳細については、stepplotを参照してください。
例
入力引数
出力引数
ヒント
アルゴリズム
内部遅延のない連続時間モデルのサンプルを取得するために、step はそのモデルを状態空間モデルに変換し、入力のゼロ次ホールドを使用してそれらのモデルを離散化します。step では、入力時間ベクトル t を t = T0:dt:Tf 形式で指定した場合を除き、システム ダイナミクスに基づいてこの離散化にサンプリング時間が自動的に選択されます。その場合、step は dt をサンプリング時間として指定します。結果として得られるシミュレーション タイム ステップ tOut は、間隔 dt で等間隔にサンプリングされます。
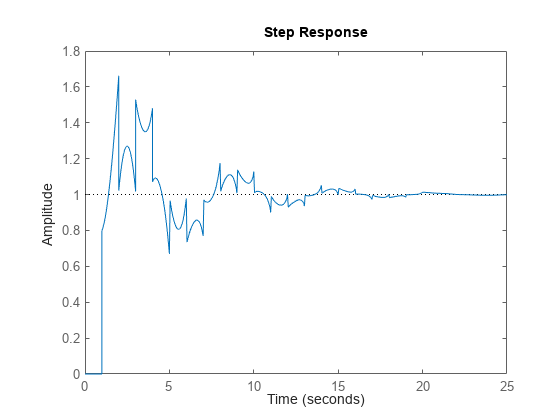
内部遅延があるシステムの場合、Control System Toolbox™ ソフトウェアは可変ステップ ソルバーを使用します。その結果、タイム ステップ tOut は等間隔にサンプリングされません。
参照
[1] L.F. Shampine and P. Gahinet, "Delay-differential-algebraic equations in control theory," Applied Numerical Mathematics, Vol. 56, Issues 3–4, pp. 574–588.