lqi

線形 2 次積分制御

構文

[K,S,e] = lqi(SYS,Q,R,N)


説明

lqi は、次の図に示すトラッキング ループに対する最適な状態フィードバック制御則を計算します。

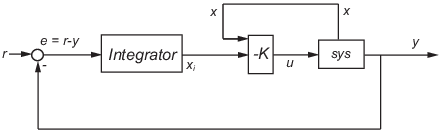
プラント sys に次の状態空間方程式 (または離散時間での等価な方程式) が成り立つとします。

$$\begin{array}{l}\frac{dx}{dt}=Ax+Bu\\ y=Cx+Du\end{array}$$

状態フィードバック制御は、次の形式となります。

$$u=-K[x;x_i]$$

ここで、x_i は積分器の出力です。この制御則は、出力 y が設定値 r を追従するようにします。MIMO システムの場合、積分器の数は、出力 y の次元と同じです。

[K,S,e] = lqi(SYS,Q,R,N) は、プラントの状態空間モデル SYS と重み行列 Q、R、N とで最適なゲイン行列 K を計算します。制御則 u = –Kz = –K[x;x_i] は、次のコスト関数を最小化します (r = 0 の場合)

• $$J(u)={\displaystyle {\int }_0^{\infty }\{z^{T}Qz+u^{T}Ru+2z^{T}Nu\}dt}$$ (連続時間)

• $$J(u)={\displaystyle \sum _{n=0}^{\infty }\{z^{T}Qz+u^{T}Ru+2z^{T}Nu\}}$$ (離散時間)

離散時間の場合、lqi は次の前進オイラー式を使用して積分器の出力 x_i を計算します。

$$x_i[n+1]=x_i[n]+Ts(r[n]-y[n])$$

ここで、Ts は SYS のサンプル時間です。

行列 N を省略すると、N は 0 に設定されます。また lqi は、関連する代数リカッチ方程式の解 S と閉ループの固有値 e を返します。

制限

拡張された積分器をもつプラントで、次の状態空間システムを考えます。

$$\begin{array}{l}\frac{\delta z}{\delta t}=A_{a}z+B_{a}u\\ y=C_{a}z+D_{a}u\end{array}$$

問題のデータは以下の条件を満たさなければなりません。

• (A,B) のペアは可安定でなければならない。

• R は正定値でなければならない。

• $$\left[\begin{array}{cc}Q& N\\ N^T& R\end{array}\right]$$ は半正定値 (つまり $$Q-N{R}^{-1}{N}^T\ge 0$$) でなければならない。

• $$\left(Q-N{R}^{-1}{N}^T,A_a-B_a{R}^{-1}{N}^T\right)$$ の虚軸 (離散時間の場合は単位円) に不可観測モードがあってはならない。

ヒント

lqi は正則な E をもつ記述子モデルをサポートします。lqi の出力 S は、次の等価な陽的状態空間モデルに対するリカッチ方程式の解です。

$$\frac{dx}{dt}=E^{-1}Ax+E^{-1}Bu$$

参考文献

[1] P. C. Young and J. C. Willems, "An approach to the linear multivariable servomechanism problem", International Journal of Control, Volume 15, Issue 5, May 1972 , pages 961–979.

バージョン履歴

R2008b で導入

参考

lqr | lqgreg | lqgtrack | lqg | care | dare